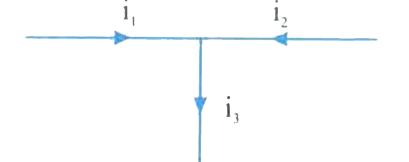
If i1=3sinωtand(i2)=4cosωt, then (i3) is

A
5sin(ωt+53∘)
B
5sin(ωt+37∘)
C
5sin(ωt+45∘)
D
5sin(ωt+35∘)
Video Solution
Text Solution
The correct Answer is:A
(i3)=(i1)+(i2)=3sinωt+4cosωt
=3sinωt+4sin(ωt+90∘)
(i30)=√I210+I220=√32+42=5
tan(ϕ)=43⇒ϕ=53∘
so, (i_3)=(I_(30) sin(omega t+phi)=5 sin (omega t+53^(@)).

|
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct
5 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- OSCILLATIONSBOOK - CENGAGE PHYSICSCHAPTER - OSCILLATIONSEXERCISE - QUESTION BANK
39 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
Knowledge Check
In the given figure, if i1=3sinωtandi2=4cost, then i3 is
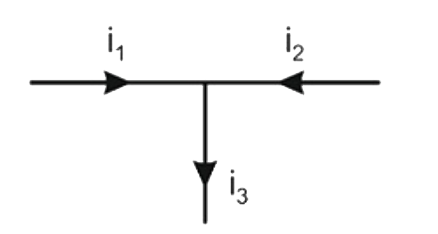 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5cos(ωt+53∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5cos(ωt+53∘)Two wave are represented by equation y1=asinωt and y2=acosωt the first wave :-
Aleads the second by πBlags the second by πCleads the second by π2Dlags the second by π2The ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
A√2B1√2C1D2
x1=3sinωt,x_(2) = 4 cos omega t
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View Solutionx1=3sinωt⇒x2=4cosωt. Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.
View SolutionThe displacements of two intering lightwaves are y1=4sinωt and y2=3cos(ωt). The amplitude of the resultant wave is (y1 and y2 are in CGS system)
View SolutionFind the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
View SolutionIf i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
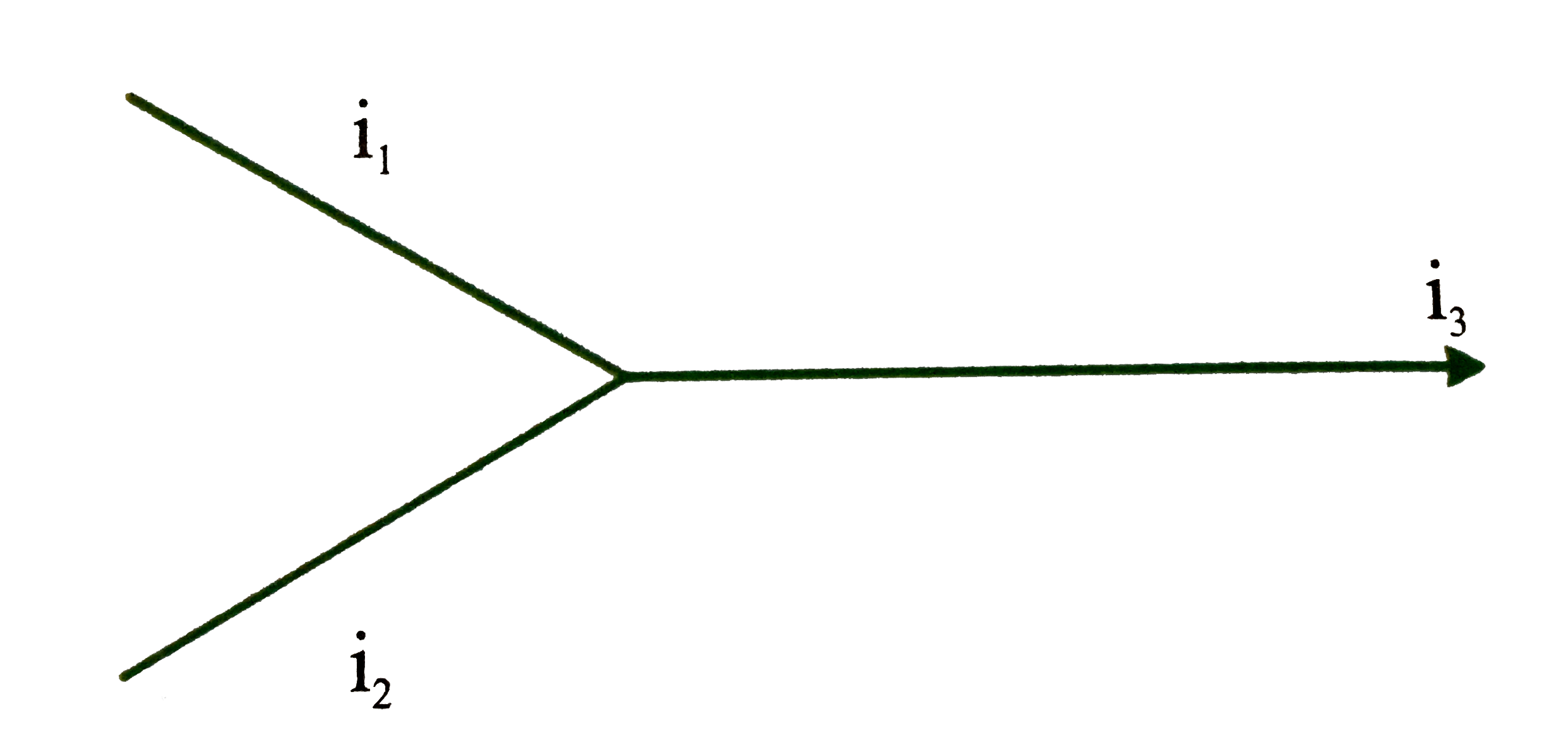
View Solution