If i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
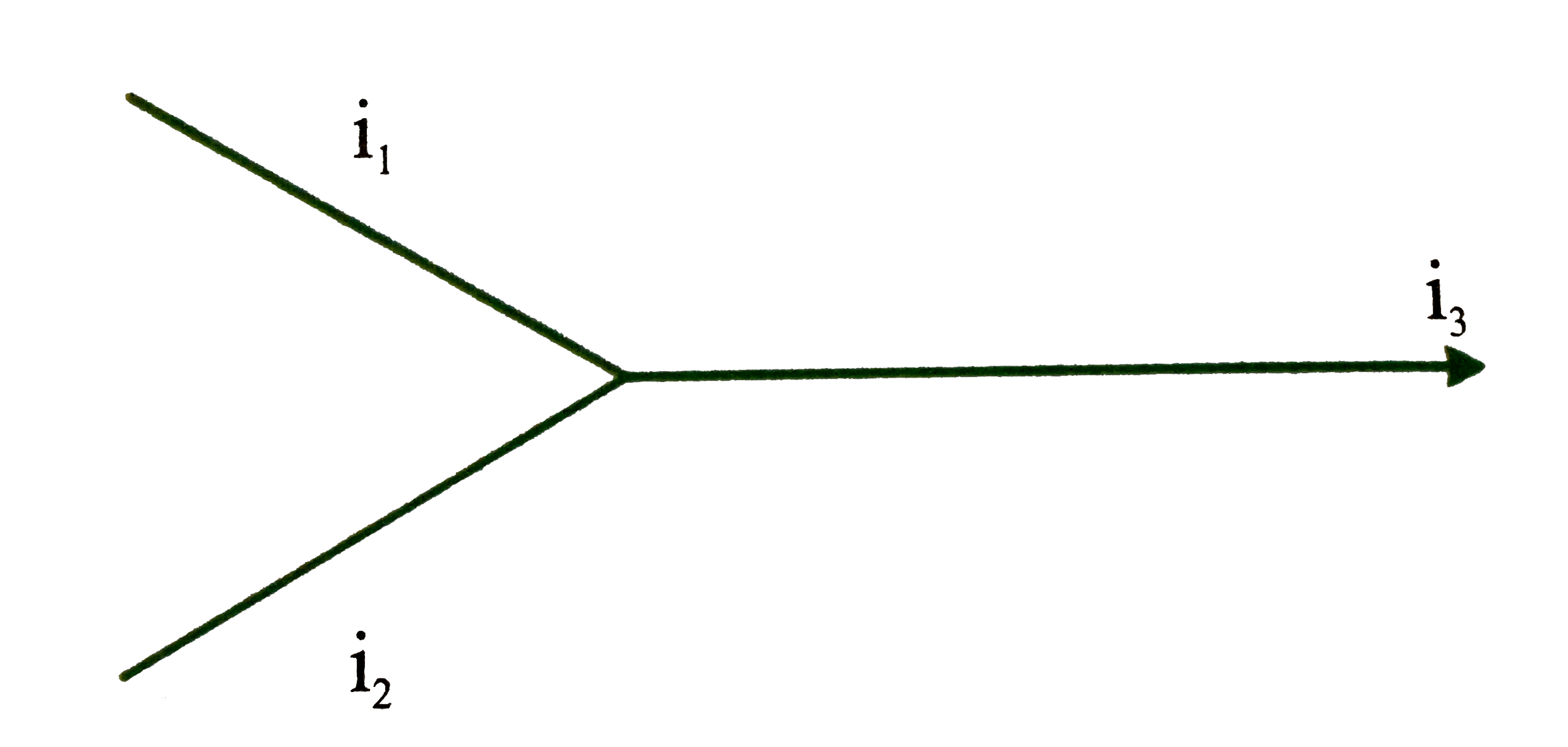
√i201+i202sin{ϕ+ωt}
(i01+i02)sin(ϕ2+ωt)
(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]
(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
The correct Answer is:D
Apply principle of superposition
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - VI
Explore 120 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - IV NCERT Based Questions
Explore 15 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
The maximum values of the phasors (currents and voltage) in AC circuits can be treated as vectors rotating with an angular frequency equal to the angular frequency of the rotor of the generator. If the phase difference between two phasors −→A1 and −→A2 is ϕ the resultant phasor is :
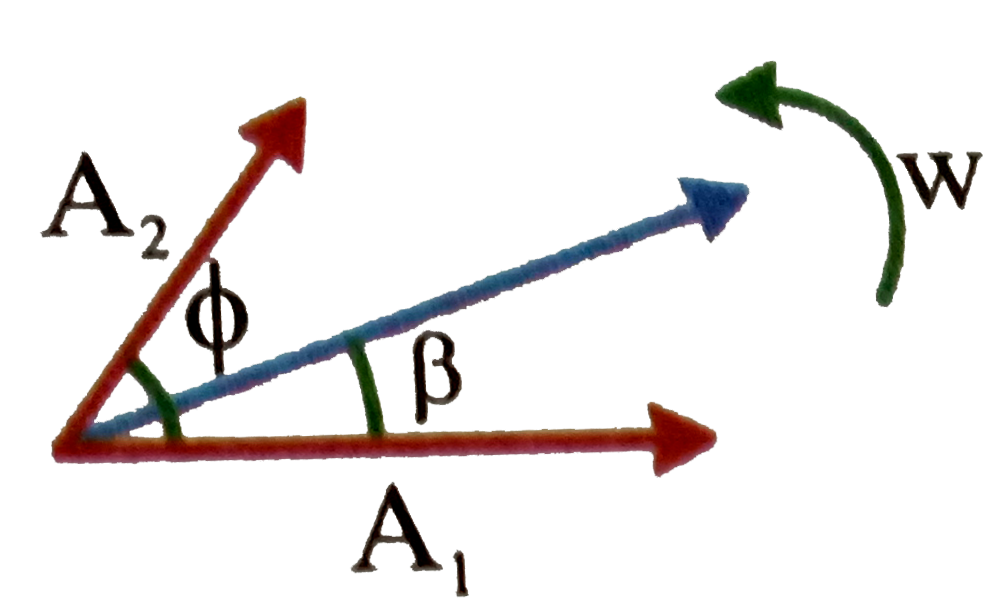
A=√A21+A22+2A1A2cosϕ
and the phase of →A with respects to A1 is
β=tan−1A2sinϕA1+A2cosϕ
RHS value
The rms value of y=f(t) is
yrms=⎧⎨⎩∫T0[f(t)]2dtT⎫⎬⎭12
Average value
The average value of y=f(t) is yav=∫T0ydtT
Using the above concept, answer the following questions.
The current i1 and i2 in A.C circuit are given as: i1=4sin(ωt−π3) and i2=4sin(ωt+π3)
The current i3 can be given as :
 A4√3sin(ωt−2π3)B2√3cos(ωt+π3)C4sin(ωt)D4cos(ωt)
A4√3sin(ωt−2π3)B2√3cos(ωt+π3)C4sin(ωt)D4cos(ωt)Four light waves are represented by
(i) y=a1sinωt
(ii) y=a2sin(ωt+φ)
(iii) y=a1sin2Ωt
(iv) y=a2sin2(ωt+φ)
Interference fringes may be observed due to superposition ofA(i) and (ii)B(i) and (iii)C(ii) and (iv)D(iii) and (iv)If i1=3sinωtand(i2)=4cosωt, then (i3) is
 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
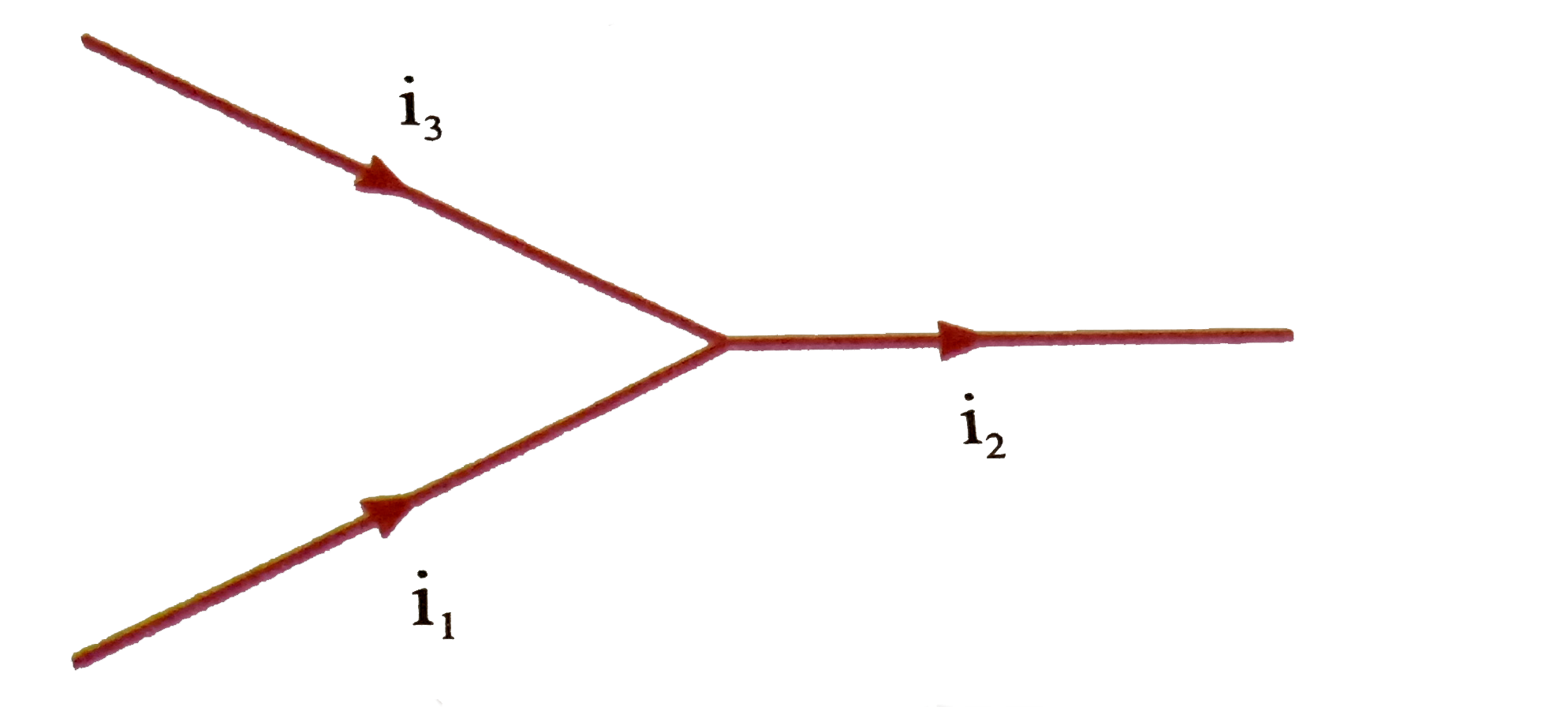
In the given figure, if i1=3sinωt and i2=4cosωt, then i3 is 5sinωt+t(φ)∘). Find ϕ
'(##CEN_KSR_PHY_JEE_C24_E01_003_Q01##)'
View SolutionIn any AC circuit the emf (e) and the current (i) at any instant are given respectively by e=E0sinωt
i=I0sin(ωt−ϕ)
The average power in the circuit over one cycle of AC is
View SolutionFour sound sources produce the following four waves
(i) y1=asin(ωt+ϕ1)
(ii) y2=asin2ωt
(iii) y3=a'sin(ωt+ϕ2)
(iv) y4=a'sin(3ωt+ϕ)
Superposition of which two waves gives rise to interference?
View SolutionIf emf and current in the circult is given by e=E0sinωt
i=l0sin(ωt−ϕ) Then the average power in the circuit over one cycle of ac is
View SolutionAn ac source producing V=V0sinωt+V0sin2ωt is connected in series with a box containing either capacitor or inductor and resistance. The current found in the circuit is I=I1sin(ωt+ϕ1)+I2sin(2ωt+ϕ2) . Here, ϕ1 and ϕ2 may be positive or negative.
View Solution


