The resonance point in XL−f and XC−f curves is
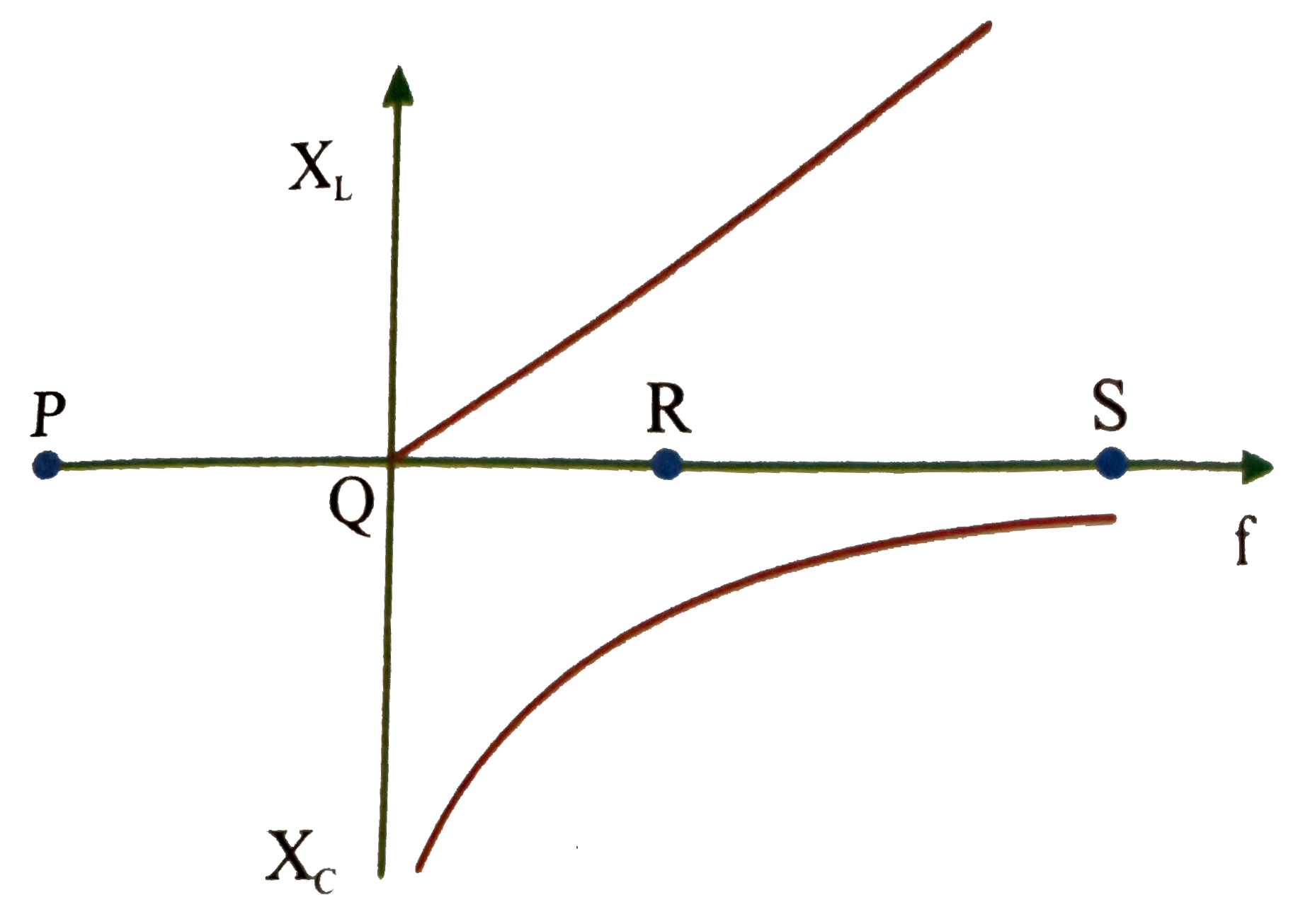
P
Q
R
S
The correct Answer is:C
Step by step video, text & image solution for The resonance point in X_(L) - f and X_(C ) - f curves is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - VI
Explore 120 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - IV NCERT Based Questions
Explore 15 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
If the tangent to the curve , y =f (x)= xlogex,(x>0) at a point (c, f(c)) is parallel to the line - segment joining the point (1,0) and (e,e) then c is equal to :
View SolutionIf y=f(x) is a curve and if there exists two points A(x1,f(x1)) and B(x2,f(x2)) on it such that f'(x1)=−1f(x2), then the tangent at x1 is normal at x2 for that curve. Now, answer the following questions.
View Solution
Knowledge Check
The figure shows variation of R,XL and XC with frequency f in a series L,C,R circuit. Then for what frequency point, the circuit is inductive ?
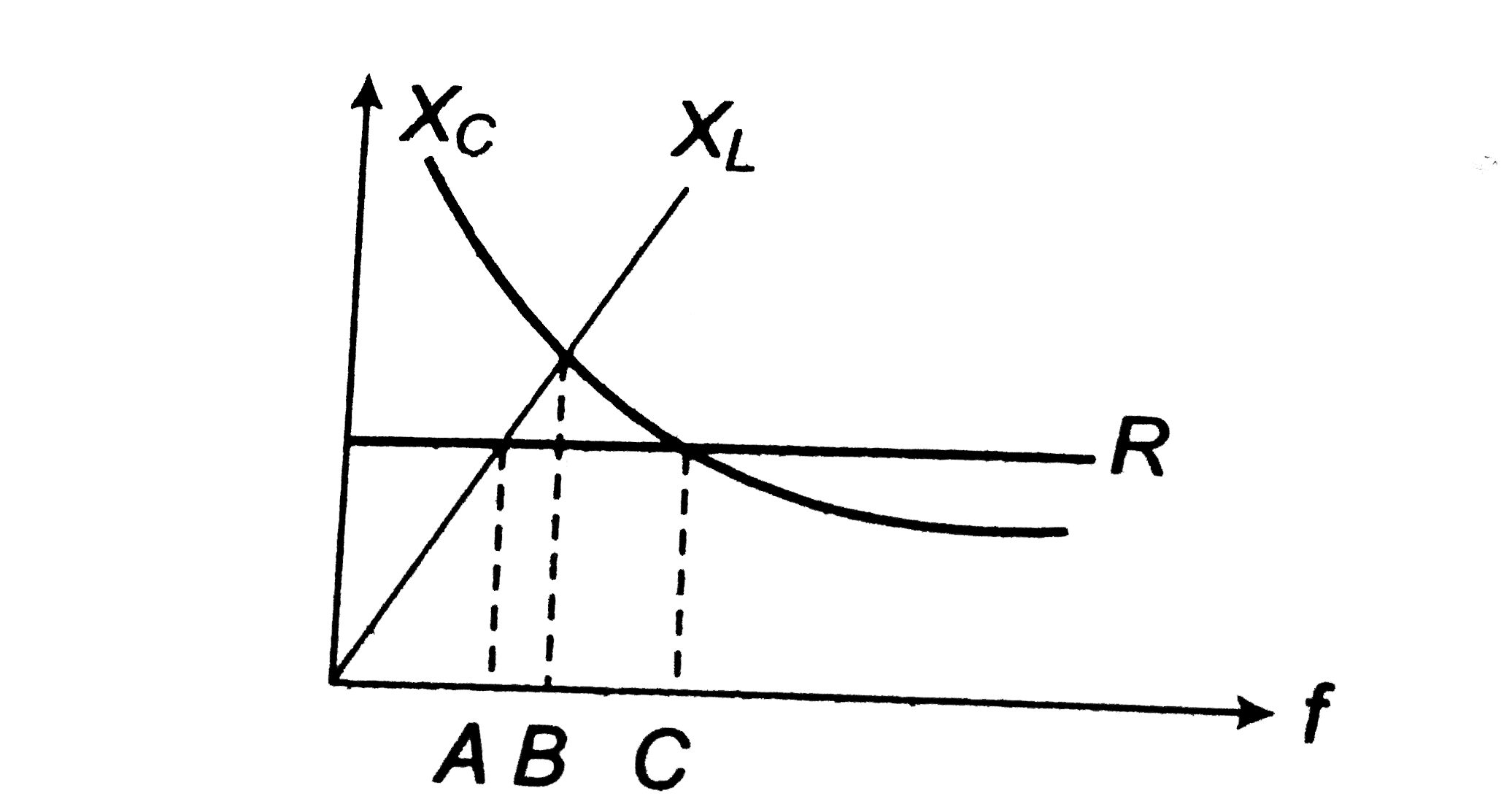 AABBCCDAll points
AABBCCDAll pointsAt an extreme point of a function f(X) the tangent to the curve is
Aparallel to the x-axisBperpendicular to the x-axisCinclined at an angle 45∘ to the x-axisDinclined at an angle 60∘ to the x-axisAt an extreme point of a function f(X) the tangent to the curve is
Aparallel to the x axisBperpendicular to the x axisCinclined at an angle 45∘ to the x axisDinclined at an angle 60∘ to the x axis
If y=f(x) is a curve and if there exists two points A(x1,f(x1)andB(x2,f(x2) on it such that f'(x1)=−1f'(x2)=f(x2)−f(x1)x2−x1, then the tangent at x1 is normal at x2 for that curve. Now, anwer the following questions.
Number of such lines on the curve y2=x3, is
View SolutionIf y=f(x) is a curve and if there exists two points A(x1,f(x1)andB(x2,f(x2) on it such that f'(x1)=−1f'(x2)=f(x2)−f(x1)x2−x1, then the tangent at x1 is normal at x2 for that curve. Now, anwer the following questions.
Number of such lines on the curve y=|lnx|, is
View SolutionThe figure shows the variation of photocurrent with anode potential for a photosensitve surface for three different radiations. Let la,lbandlc be the curves a, b and c, respectively

(a) fa=fbandla≠lb (b) fa=fcandla=lc
(c ) fa=fbandla=lb (d) fb=fcandlb=lc
View SolutionThe length of tangent at a point P(x1,y1) to the curve y=f(x) ,having slope m at P is
View SolutionIf the tangent line at a point (x, y) on the curve y=f(x) is parallel to x-axis, then write the value of dydx .
View Solution

