A block of mass m1=1kg is attached to a spring of force constant k=24N/cm at one end and attached to a string tensioned by mass m2=5kg . Dedcue the frequency of oscillaitons of the system. If m2 is initially supported in hand and then suddenly released, find

(a) instantaneous tension just after m2 is released . ltbr> (b) the maximum displacement of m1.
(c) the maximum and minimum tensions in the string during oscillations.
The correct Answer is:A, B, C
T=2π√m1+m2K
=2π√62400=π10
⇒f=10π
Instantaneous tension just after m2 is released will be zero as the spring is unstressed.
Amplitude of m1=m2g/K=25/12cm, hence maximum displacement of m1 will be 25/6cm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 75
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 76
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp73
Explore 4 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionTwo bodies with masses m1 = 1kg and m2= 2kg are connected by a spring of force constant k=24Nm−1. The left ball is imparted an initial velocity v0=12 cm/s. Find (a) the frequency of the oscillations (b) the energy and the amplitude of the osciallations.
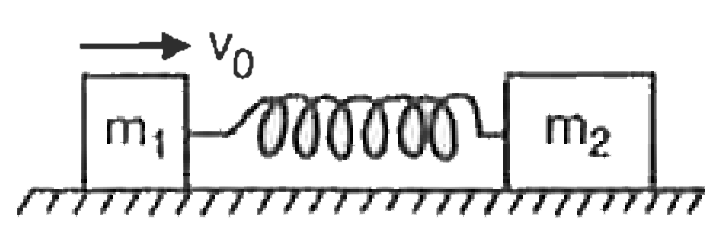
View Solution
Knowledge Check
An ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
A4mgkB2MgkCMgkDMg2kTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cmA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
A11B7C6D15
A block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View SolutionTwo blocks of mass m1andm2 are connected by a spring of force constant k. Block of mass m1 os pulled by a constant force f2 [see fig 4E.19 (a)] find the maximum elongation in the spring .
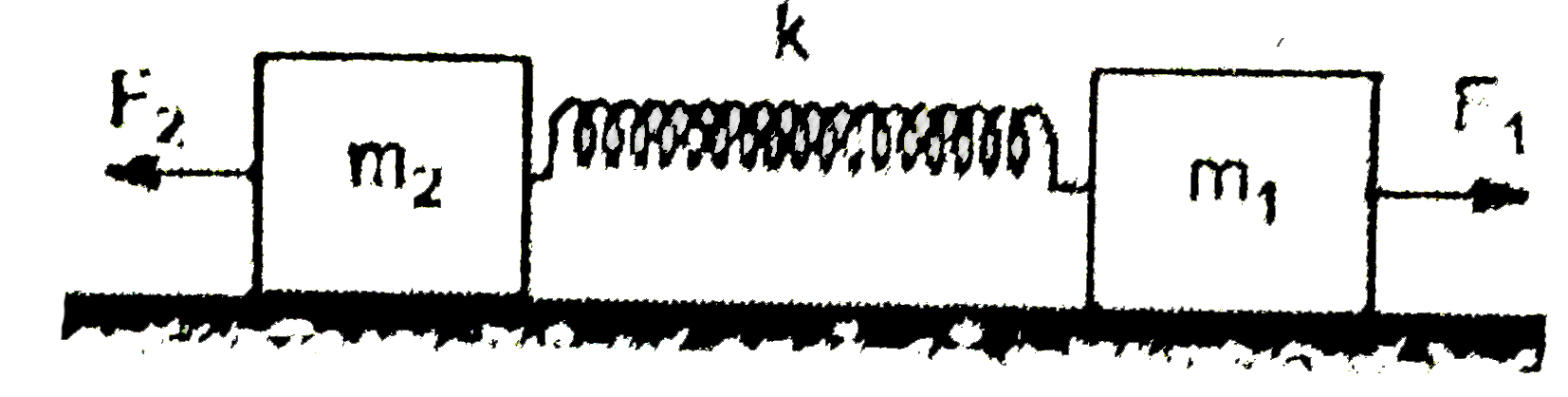
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
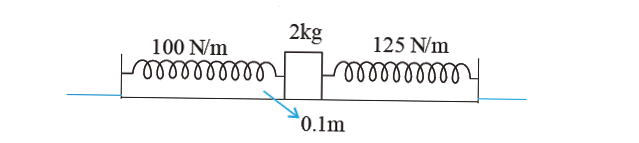
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View Solution

