A uniform chain of mass m and length l hanges on a thread and touches the surface of a table by its lower end. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap.

The correct Answer is:32
1. Weight of the portion BC of the chain lying on the table, W=mg2 (downwards) Using v=√2gh
2. Thrust force Ft=vr(dmdt)
vf=v
dmdt=λv
Ft=λv2
(where λ=ml, is mass per unit length of chaing)
v2=(√gl)2=gl
∴Ft=(ml)(gl)=mg (downward)
∴ Net force exerted by the chain on the table is
F=W+Ft=mg2+mg=32mg
So, from Newton's third law the force exerted by the table on the chain will be 32mg (vertically upwards).
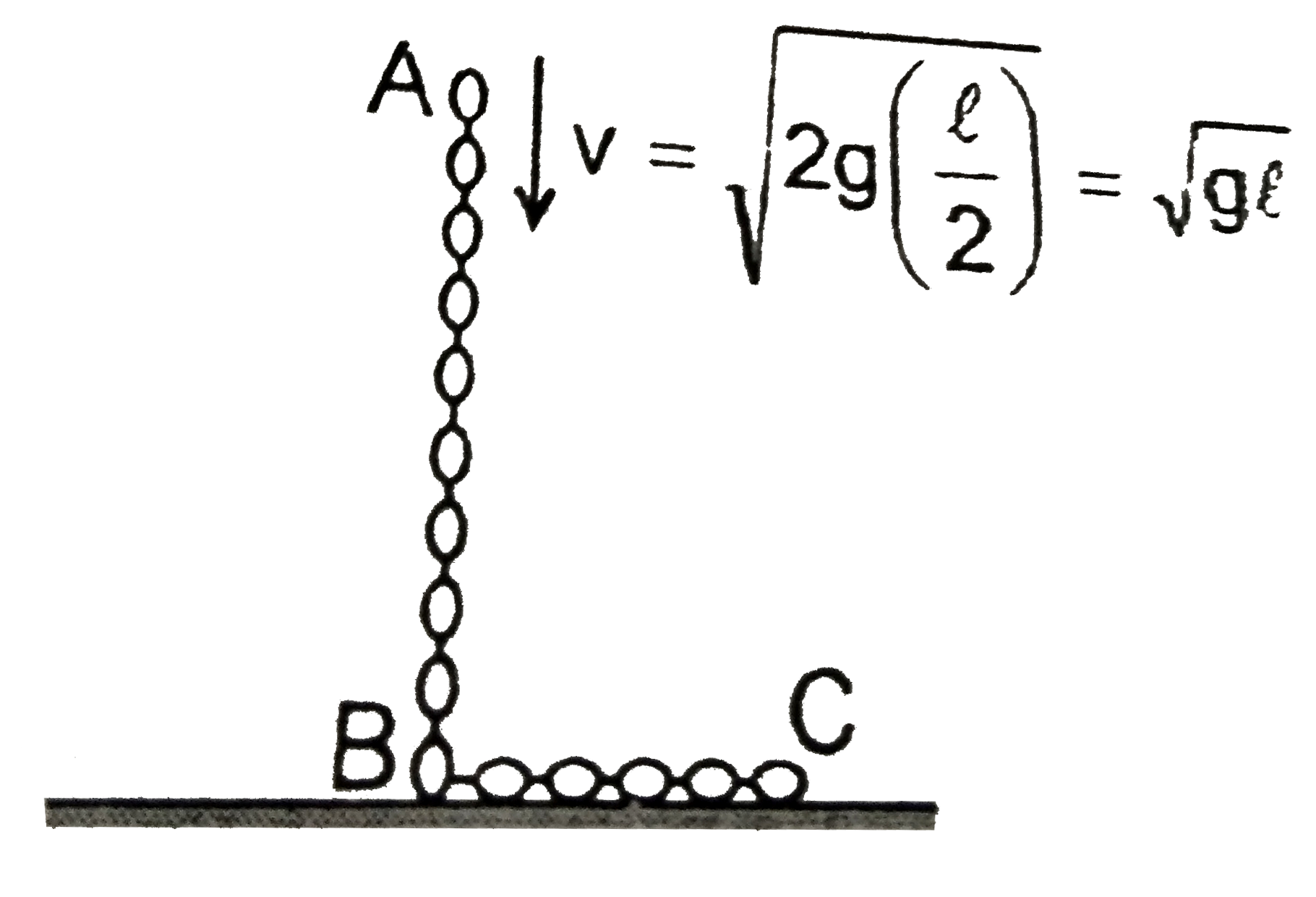
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 62
Explore 4 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 63
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 60
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A chain hangs on a thread and touches the surface of a table by its lower end. Show that after the thread has been burned through, the force exerted on the table by the falling part of the chain at any moment is twice as great as the force of pressure exerted by the part already resting on the table.
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View Solution
Knowledge Check
A uniform chain of mass m and length l hangs on a thread and touches the surface of a table by its lower end. Thread breaks suddenly. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap
 Amg2B3mg2CmgDNone of these
Amg2B3mg2CmgDNone of theseA uniform chain of mass m hangs from a light pulley, with unequal lengths of the chain hanging from the two sides of the pulley. The force exerted by the moving chain on the pulley is
AmgB>mgC<mgDeither (b) or (c) depending of the chain
A uniform chain of mass m and length l overhangs a table with its two third part on the table. Fine the work to be done by a person to put the hanging part back on the table.
View SolutionA uniform chain of length l begins to fall with a velocity v on the table. Find the thrust force exerted by the chain on the table.
View SolutionA unifrom chain of mass M and length L lies on a table with nth part of it hanging off the table. Find the work required to slowly pull the hanging part up to the table.

View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
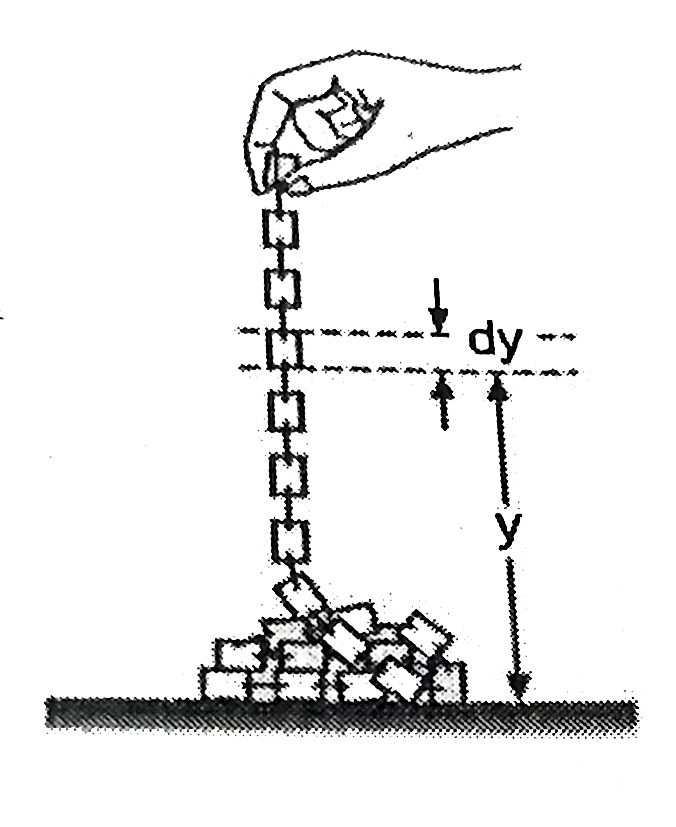
View SolutionA very flexible unifrom chain of mass M and length L is suspended vertically so that its lower end just touches the surface of a table When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table Find the force exerted by the chain on the table at the moment when x part of chain has already rested on the table .
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
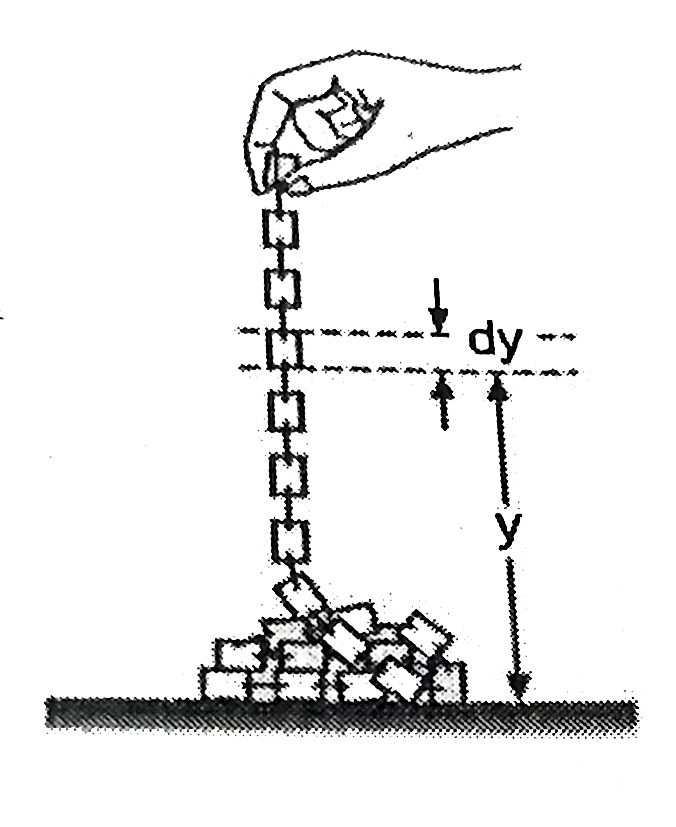
View Solution