The angular velocity of a rigid body about any point of that body is same :
only in magnitude
only in direction
both in magnitude and direction necessarily
both in magnitude and direction about some points but not about all points.
The correct Answer is:C
Suppose a rod is having angular velocity ω about point C.
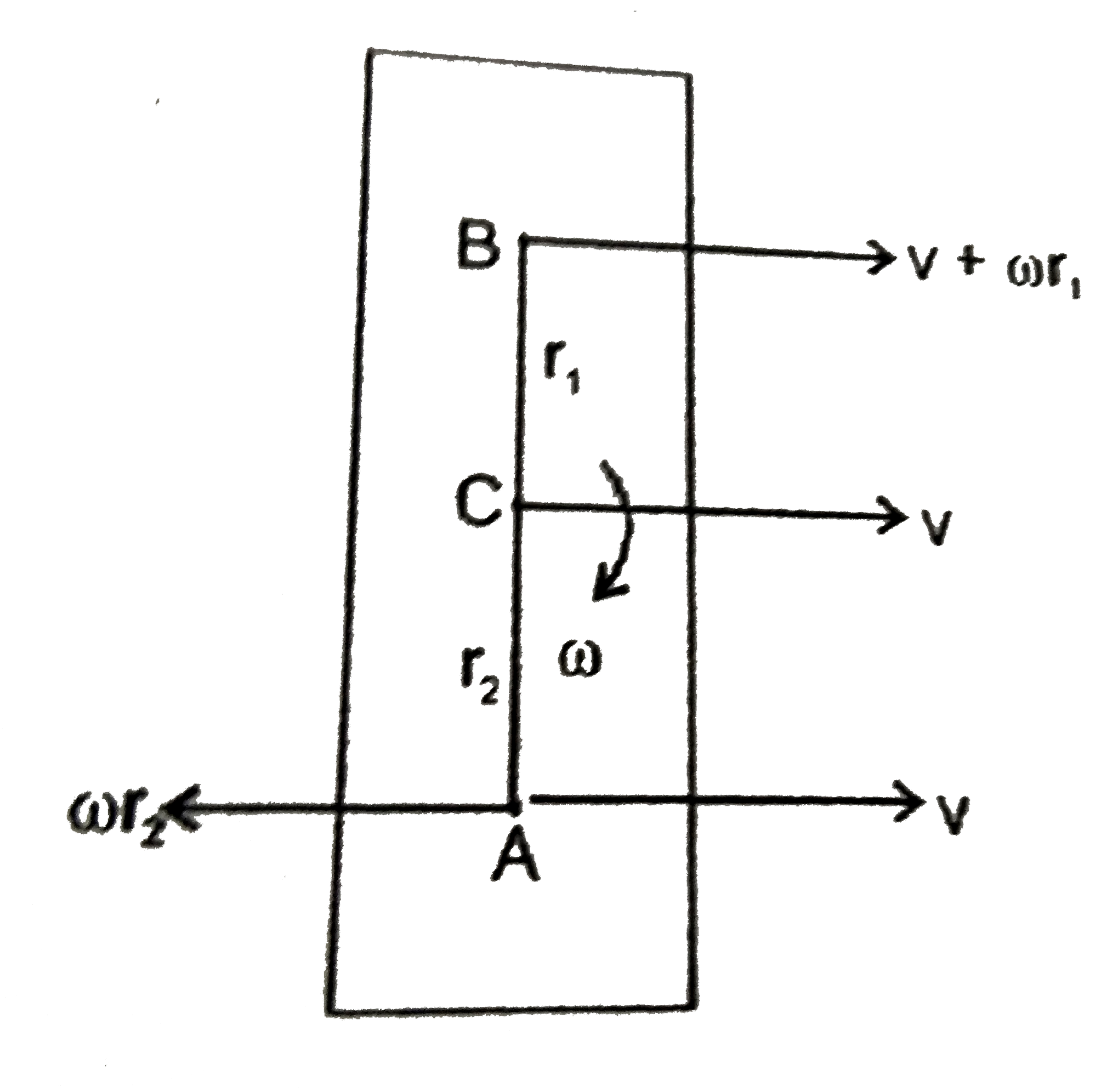
Choose two points A and B as shown in the figure. Velocity of Bw.r.t.A=(v+ωr1)−(v−ωr2)
=VBA=ω(r1+r2)
Angular velocity of Bw.r.t.A=vBAAB
=ω(r1+r2)r1+r2=ωAns(C)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 62
Explore 4 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 63
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 60
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
The angular velocity of a rigid body is 24 rad s−1, Calculate the time it will take to rotate 72 rad.
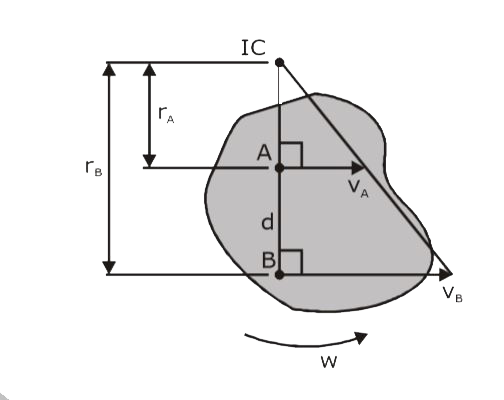
View SolutionConsider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are parallel and pointing in the same direction. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem.
Note that lC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors vAandvB
View Solution
Knowledge Check
The angular momentum of a rigid body is
Athe moment of the acting force.Bmoment of the momentum.Cmoment of the mass.Dmoment of the acceleration.Assertion : The angular velocity of a rigid body in motion is defined for the whole body
Reason : All points on a rigid body performing pure rotational motion are having same angular velocity.AIf both Assertion and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is fasleDIf Assertion is false but Reason is trueA : When a rigid body rotates about any fixed axis, then all the particles of it move in circles of different radii but with same angular velocity.
R : In rigid body relative position of particles are fixed.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion,BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion,CIf Assertion is true statement but Reason is false,DIf both Assertion and Reason are false statements,
A rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View SolutionIf the angular velocity of a rotating rigid body is increased then its moment of inertia about that axis
View SolutionA body of moment of inertia about its axis of rotation is 3kgm2 and angular velocity 3 rad/s. The kinetic energy of rotating body is same as that of body of mass 27 kg moving with a speed of
View SolutionConsider the following two statements A and B and identify the correct choice
A) When a rigid body is rotating about its own axis, at a given instant all particles of body posses same angular velocity.
B) When a rigid body is rotating about its own axis, the linear velocity of a particle is directly proportional to its perpendicular distance from axis
View Solution

