A ball of mass m=200gm is suspended from a point A by an inextensible string of length L. Ball is drawn to a side and held at same level as A but at a distance √32L from A as shown. Now the ball is released. Then :( assume string applies only that much jerk which is required so that velocity along string becomes zero ).

speed of ball just before experiencing jerk is √gL
speed of ball just after experiencing jerk is √3gL2
Impulse applied by string √gL10
ball will experience jerk after reaching to point B.
The correct Answer is:A, B, C
By conservation of energy
12mv2=mgL2
v=√gL
After jerk vsinθ becomes zero
Impulse applied by string =mvsinθ

=0.2√gL12=√gL10
velocity of ball after jerk
vcosθ=√gL√32=√3gL2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 55
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 56
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 53
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
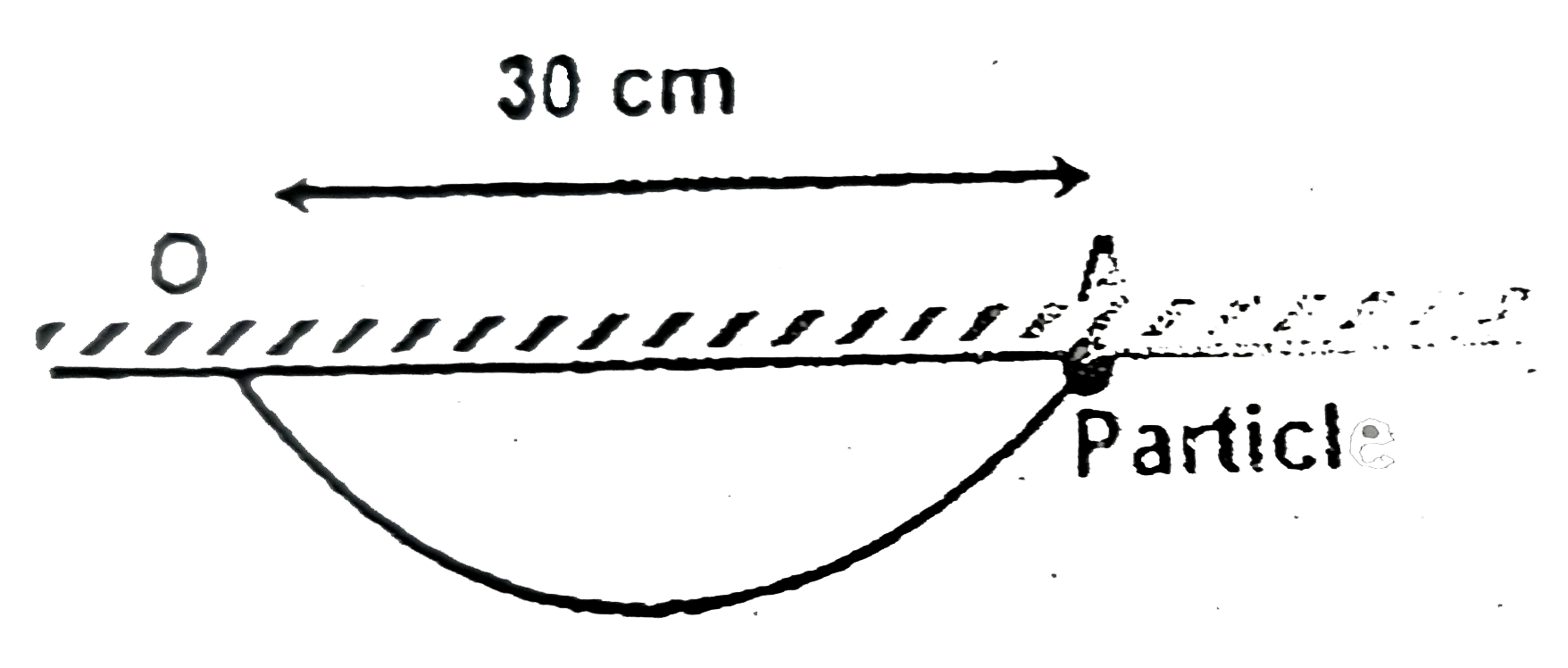
A small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
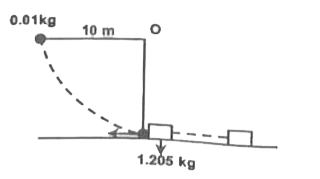
View SolutionA ball of mass 0.01 kg is suspended from a fixed point O by means of a light and inextensible string of length 10m. The ball is first taken aside such that string becomes horizontal and then released from reast. At the lowermost point of its path, it hits a stationary small block of mass 1.205kg lying on a rough horizontal surface. After striking the block, the ball rebounds and comes to rest when the string makes an angle of 30∘) with the horizontal . Due to the impact the block moves through a distance of 0.5m on the horizontal surface. Find the coefficient of friction between the block and the surface.
View Solution
Knowledge Check
Two balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
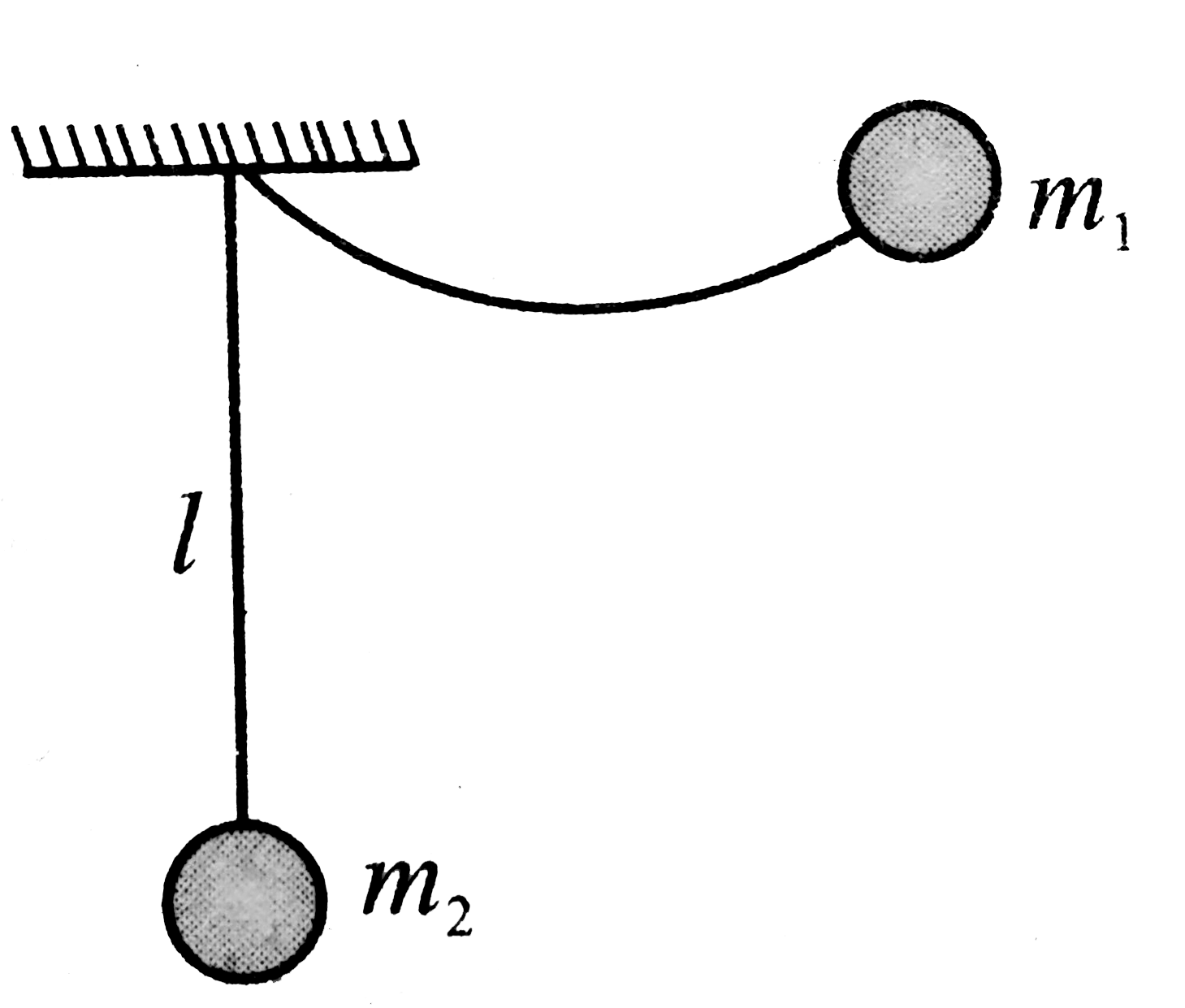
Velocity u1 with which the hall of mass m1 collides with the other ball isA1m/sB2m/sC3m/sD4m/sTwo balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
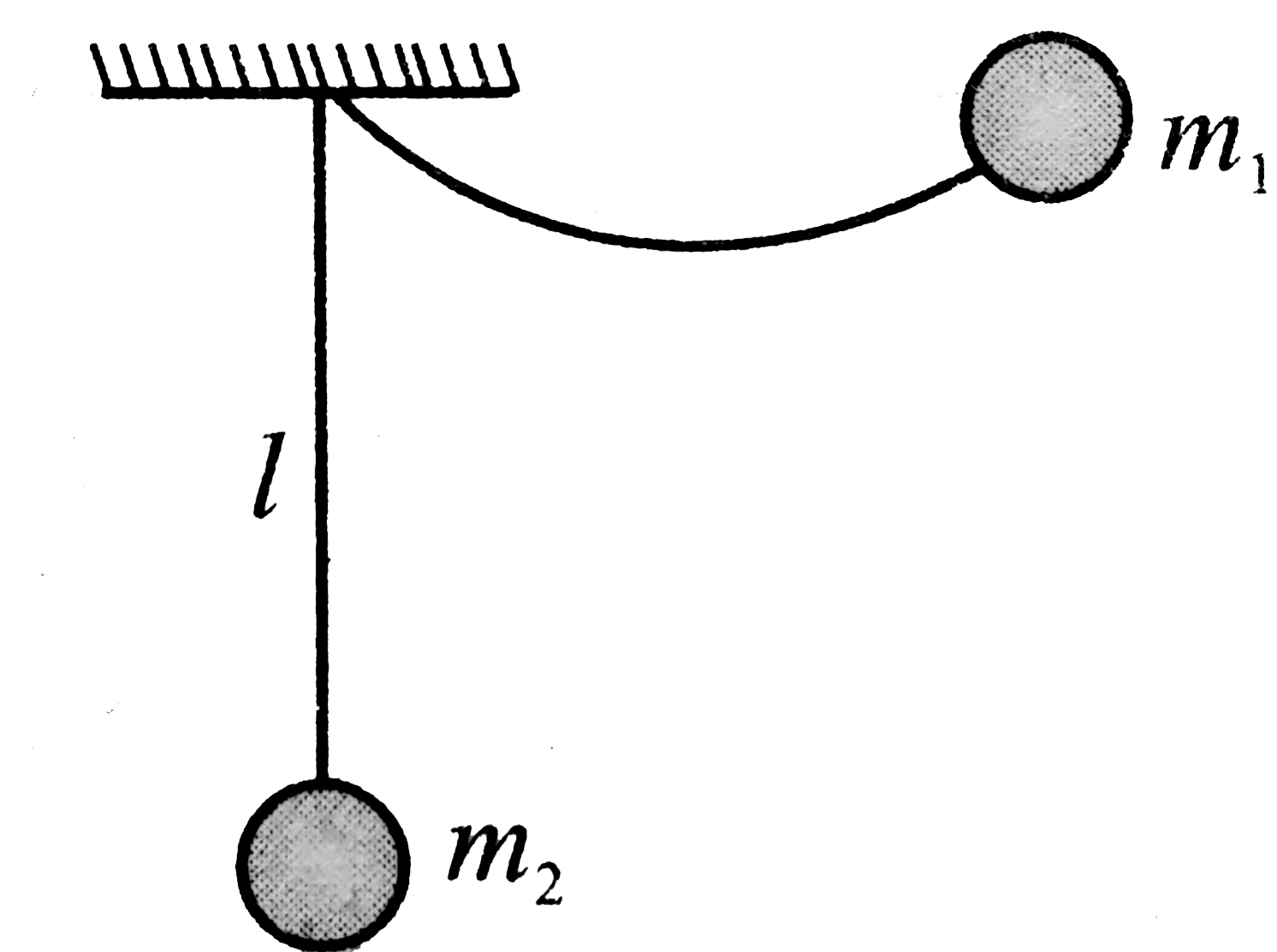 The maximum rise of centre of mass of the ball of massm2 isA0.20mB0.50mC0.75mD1m
The maximum rise of centre of mass of the ball of massm2 isA0.20mB0.50mC0.75mD1mA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
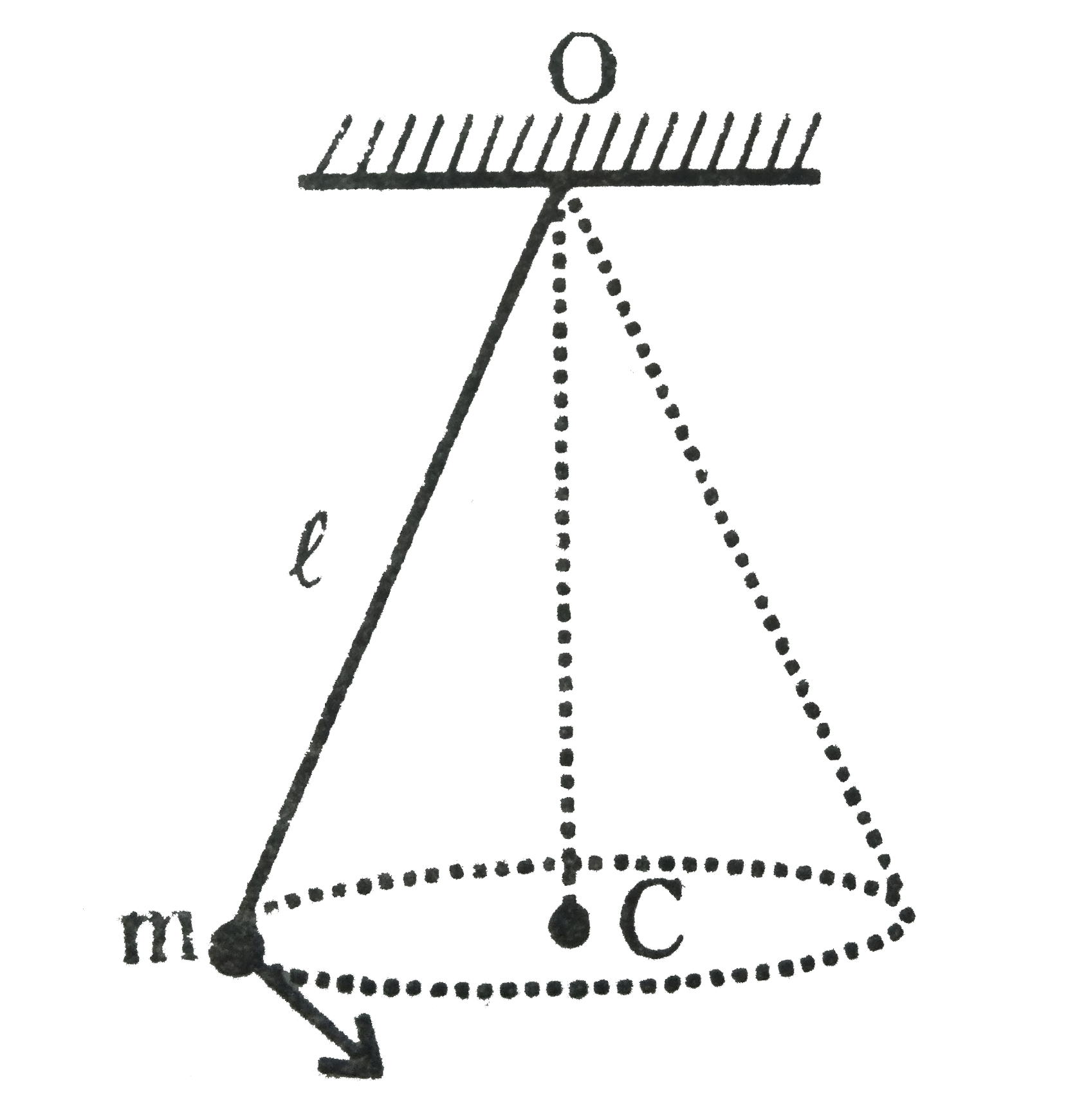 .Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
.Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
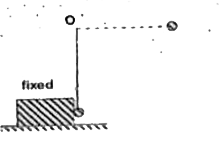
View SolutionA uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :

View SolutionA ball of mass M is rotating in a conical pendulum by a string of length L. If radius of circular path is L√2, find the velocity of mass
View SolutionA string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
View Solution

