For a two − body sstem in absence of external forces, the kinetic energy as measured from ground frame is K0 and from centre of mass frame is Kcm. Pick up the wrong statement.
The kinetic energy as measured from center of mass frame is least
Only the portion of energy Kcm can be transferred from one form to another due to internal changes in the system.
The system always retains at least Ko−Kcm amount of kinetic energy as measured from ground frame irrespective of any kind of internal changes in the system.
The system always retains at least Kcm amount of kinetic energy as measured from ground frame irrespective of any kind of internal changes in the system.
The correct Answer is:D
It can be shown that
K0=Kcm+12WV2cm where M is the total mass of the system and Vcm is velocity of centre of mass with respect to ground.
Due to internal changes Kcm can change but Vcm will remain same. Hence only Kcm portion of kintic energy can be transformed to some other form of energy. Thus D is the wrong statement.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 55
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 56
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 53
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Two particles having masses m1andm2 are moving with velocities →V1and→V2 respectively. →V0 is velocity of centre of mass of the system.
(a) Prove that the kinetic energy of the system in a reference frame attached to the centre of mass of the system is KEcm=12μV2rel. Where μ=m1m2m1+m2 and Vrel is the relative speed of the two particles.
(b) Prove that the kinetic energy of the system in ground frame is given by
KE=KEcm+12(m1+m2)V20
(c) If the two particles collide head on find the minimum kinetic energy that the system has during collision.
View SolutionFind the kinetic energy needed to project a body of mass m from the centre of a ring of mass M and radius R so that it will never comne back.
View Solution
Knowledge Check
If there are no external forces, the centre of mass of a double star moves like a free particle.
If we go to the centre of mass frame, then we find that the two starts are moving in a circle about the centre of mass, which is at rest.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.A body is orbiting very close to the earth surface kinetic energy K.E. The energy required to completely escape from it is
A√2K.EB2K.E.CK.E.√2DNone of theseAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

What is the loss in the energy of the system due to breaking of B?A38kx2B34kx2C18kx2D58kx2
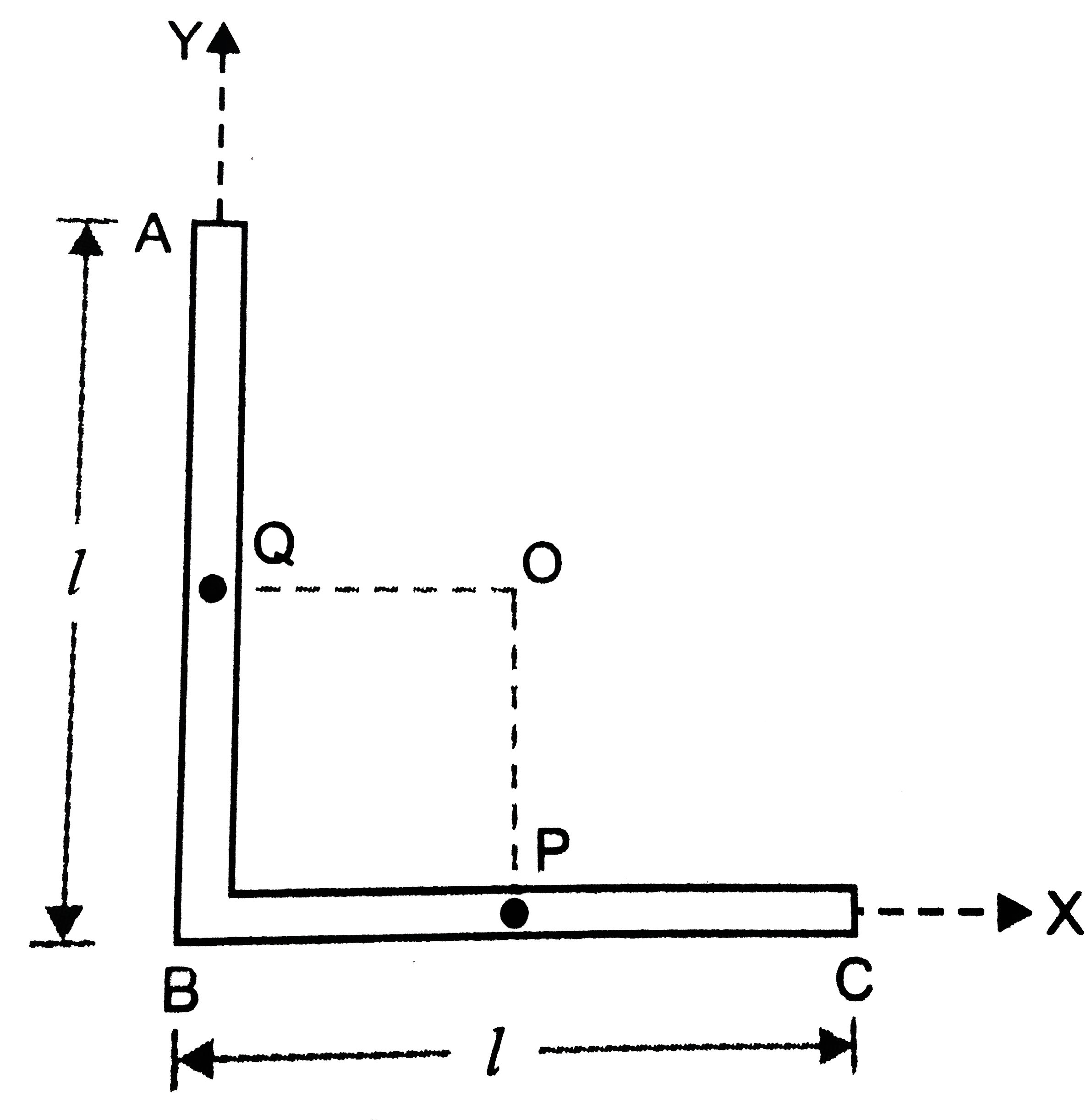
Two identical uniform rods of length l are joined to from L shaped frame, as shown is Fig. Locate the centre of mass of the frame.
View SolutionTwo masses, m1 and m2 , are moving with velocities v1 and v2. Find their total kinetic energy in the reference frame of centre of mass.
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.
View SolutionStatement-1: In centre of mass frame the linear momentum of system is conserved only if no external forces are present
Statement-2: In presence of external force, the centre of mass has acceleration in inertial frame equal to Σ→Fextm→tal
View Solution

