A ball of mass M is rotating in a conical pendulum by a string of length L. If radius of circular path is L√2, find the velocity of mass
√gL
√gL2
√2gL
√gL√2
The correct Answer is:D
To find the velocity of a ball of mass M rotating in a conical pendulum with a string of length L and a radius of circular path L√2, we can follow these steps:
1. Identify the Components of Forces:
- The tension T in the string can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
- Here, θ is the angle the string makes with the vertical.
2. Determine the Angle:
- Given that the radius of the circular path is L√2, we can find the angle θ.
- In a conical pendulum, the relationship between the radius r, the length of the string L, and the angle θ is given by:
r=Lsinθ
- Thus, we have:
L√2=Lsinθ⟹sinθ=1√2⟹θ=45∘
3. Apply Newton's Second Law:
- In the vertical direction, the forces must balance:
Tcosθ=Mg
- In the horizontal direction, the net force provides the centripetal force:
Tsinθ=Mv2r
4. Substitute the Known Values:
- Substitute r=L√2 and θ=45∘ into the equations:
- For the vertical direction:
Tcos45∘=Mg⟹T1√2=Mg⟹T=Mg√2
- For the horizontal direction:
Tsin45∘=Mv2L√2⟹T1√2=Mv2√2L
5. Equate the Tension Expressions:
- Substitute T=Mg√2 into the horizontal equation:
Mg√2⋅1√2=Mv2√2L
- This simplifies to:
Mg=Mv2√2L
6. Cancel Mass M:
- Since M is non-zero, we can cancel it from both sides:
g=v2√2L
7. Solve for Velocity v:
- Rearranging gives:
v2=gL√2⟹v=√gL√2
Final Result:
Thus, the velocity of the mass v is:
v=√gL√2
- The tension T in the string can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
- Here, θ is the angle the string makes with the vertical.
- Given that the radius of the circular path is L√2, we can find the angle θ.
- In a conical pendulum, the relationship between the radius r, the length of the string L, and the angle θ is given by:
r=Lsinθ
- Thus, we have:
L√2=Lsinθ⟹sinθ=1√2⟹θ=45∘
- In the vertical direction, the forces must balance:
Tcosθ=Mg
- In the horizontal direction, the net force provides the centripetal force:
Tsinθ=Mv2r
- Substitute r=L√2 and θ=45∘ into the equations:
- For the vertical direction:
Tcos45∘=Mg⟹T1√2=Mg⟹T=Mg√2
- For the horizontal direction:
Tsin45∘=Mv2L√2⟹T1√2=Mv2√2L
- Substitute T=Mg√2 into the horizontal equation:
Mg√2⋅1√2=Mv2√2L
- This simplifies to:
Mg=Mv2√2L
- Since M is non-zero, we can cancel it from both sides:
g=v2√2L
- Rearranging gives:
v2=gL√2⟹v=√gL√2
Thus, the velocity of the mass v is:
v=√gL√2
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A ball of mass m = 0.5 kg is attached to the end of a string having length L = 0.5 is rotated on a horizontal circular path about the vertical axis. The maximum tension that the string can bear is 324N.What is the maximum possible value of angular velocity of ball ( in radian / s ) ?
View SolutionA ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
View Solution
Knowledge Check
For a conical pendulum of string length L, its angular speed is proportional to
A√LBLC1√LD1LA stone of mass ied to a string of lengh l rotating along & a circular path with constant speed v. The torque on the stone is
Amv2lBmvlCmvlDzeroA stone of mass 1kg tied to a light inextensible sstring of length L=10m is whirling in a circular path of radius L in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if g is taken to be 10ms−2 , the speed of the stone at the highest point of the circle is.
A10ms−1B5√2ms−1C10√3DNone of these
In the previous problem , the block of massM is attached to a string of length L. Find the maximum angle made by the string with vertical . Take veloctiy of buller u=4√gL. Take M=3m.
View SolutionA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
View SolutionA particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
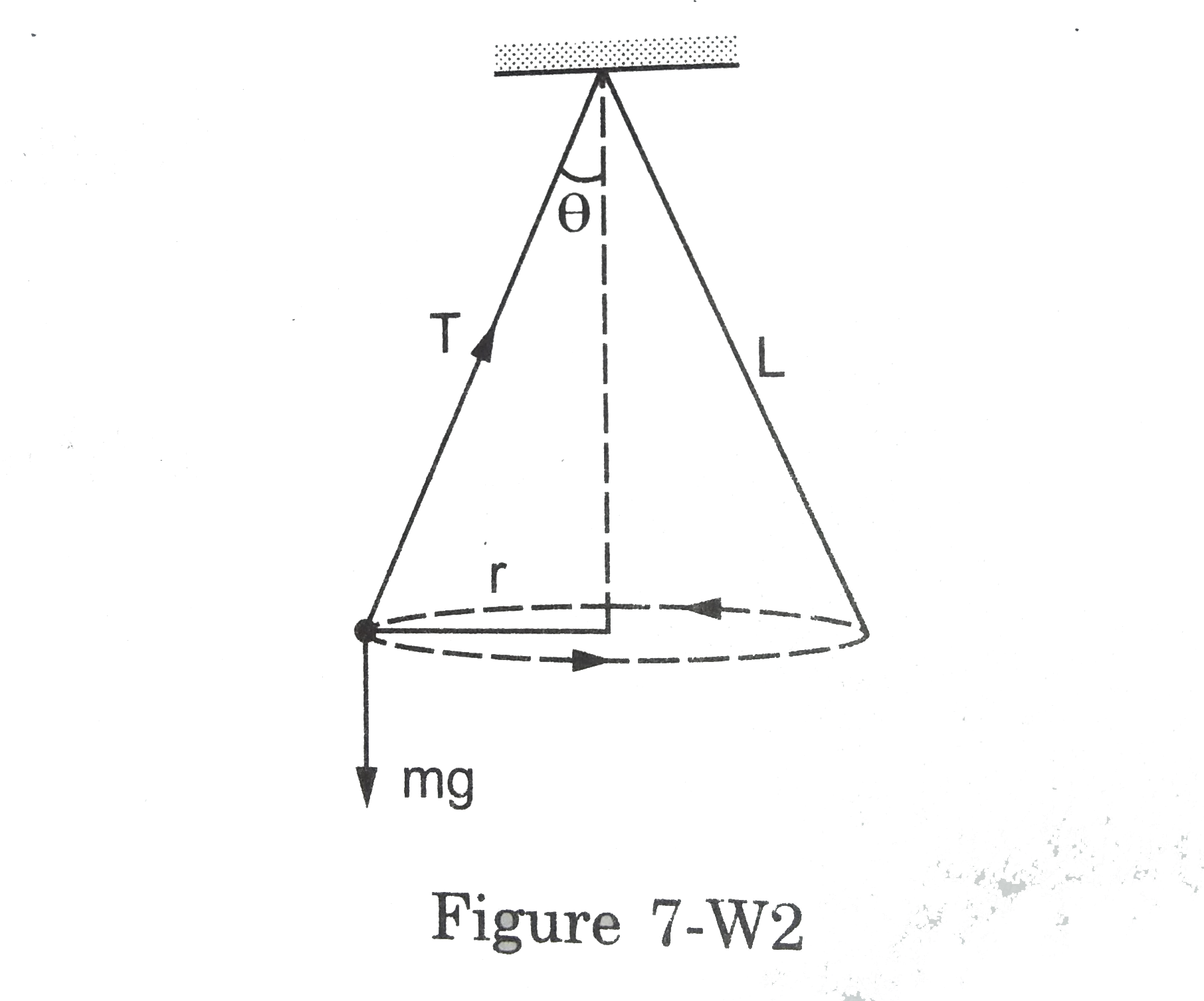
.
View SolutionIf a stone of mass m is rotated in a vertical circular path of radius 1m, the critical velocity is
View SolutionA body of mass 2 kg is rotating on a circular path of radius 0.5 m, with an angular velocity of 20 rad/s. If the radius of the path is doubled, then the new angular velocity will be
View Solution
