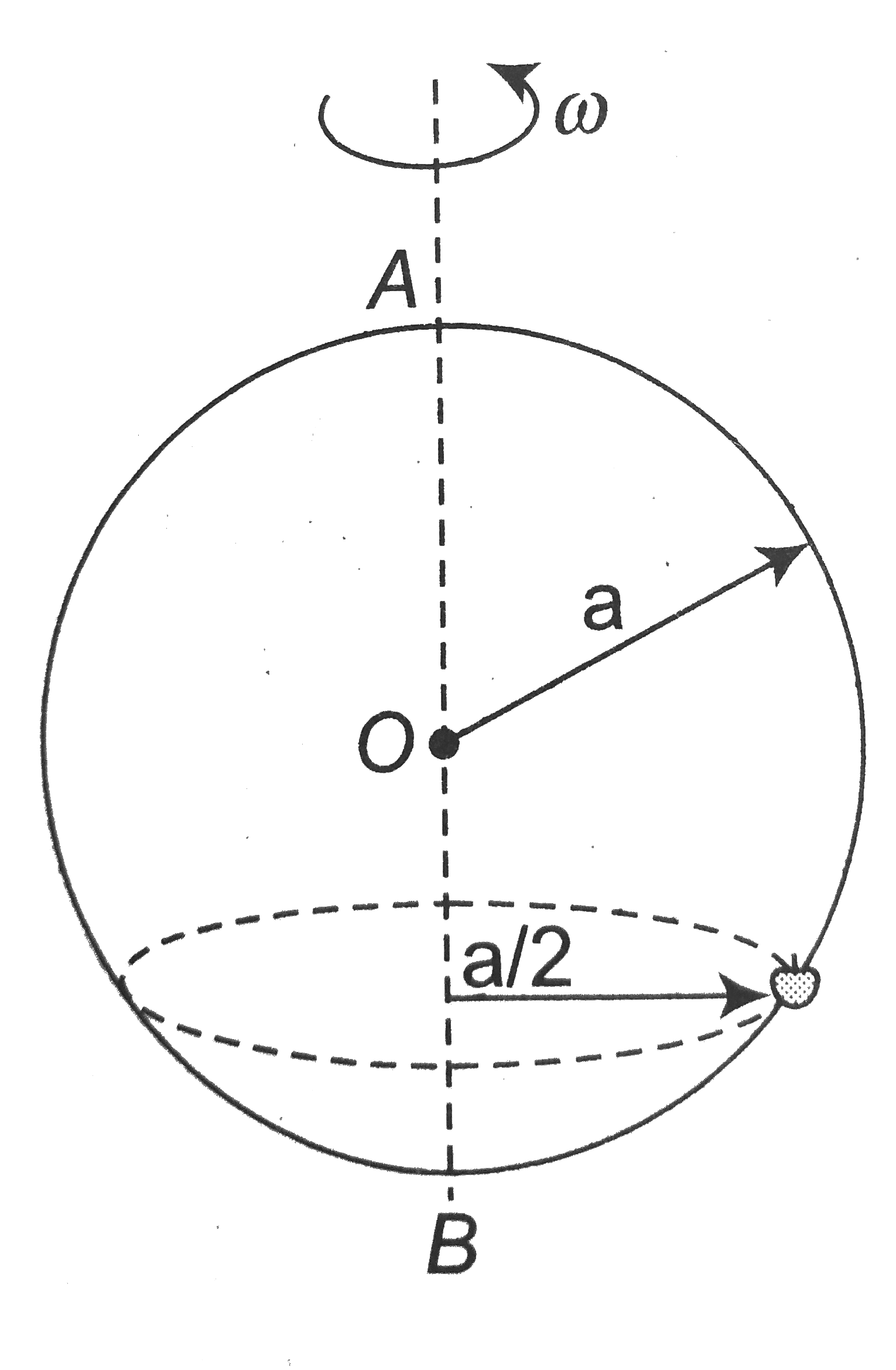
A smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:
2ga
2ga√3
g√3a
2ag√3
The correct Answer is:B
As ,cosθ=a2a
θ=60∘
∴Nsin60∘=mg
Ncos60∘=mω2a2
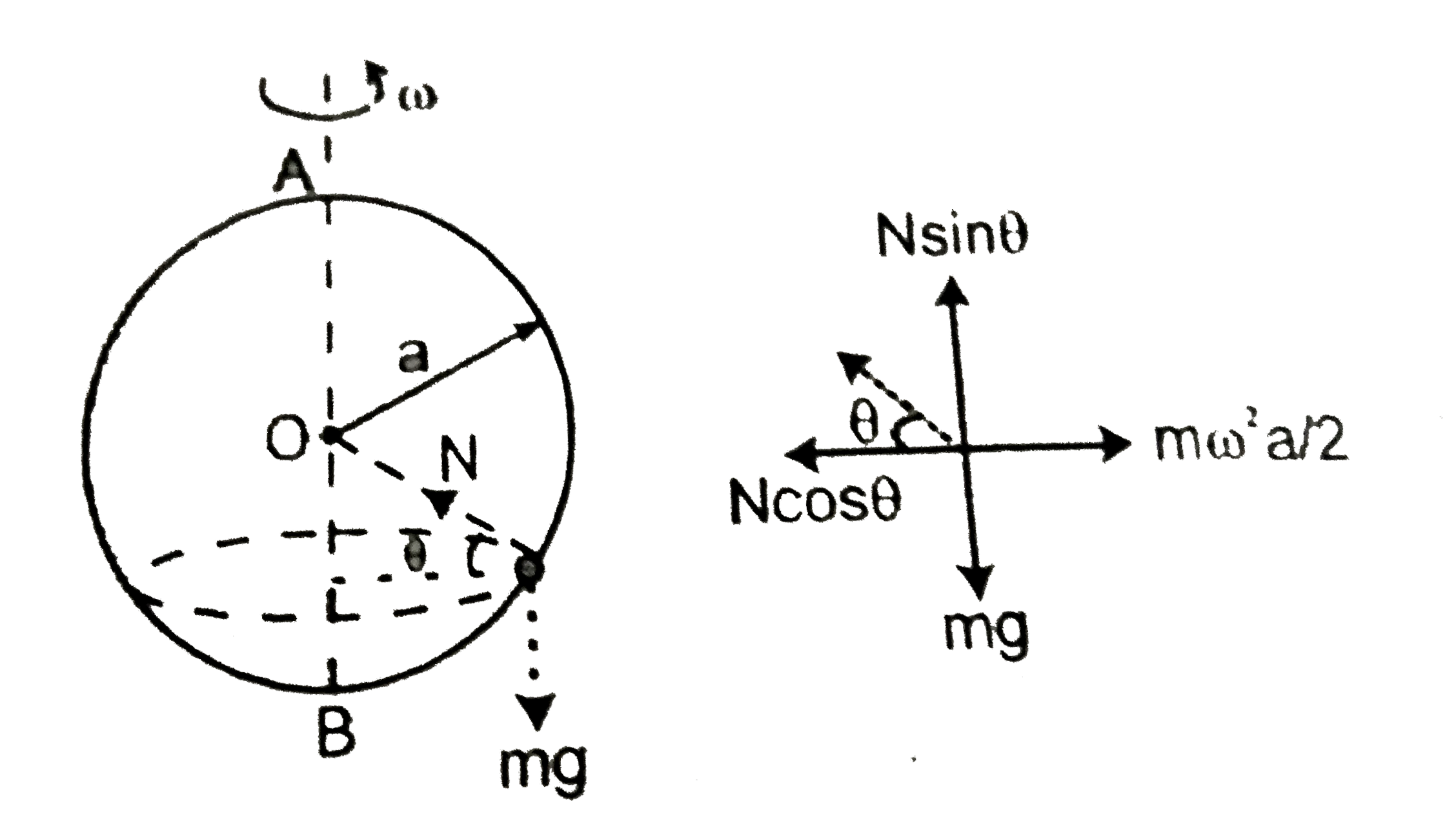
w.r.t. wire
∴tan60∘=2gω2a,ω2=2ga√3
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 45
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 46
Explore 6 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 43
Explore 11 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
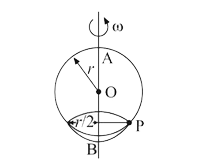
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
View SolutionA circular loop has a small bead which can slide on it without friction. The radius of the loop is r. Keeping the loop vertically it is rotated about a vertical diameter at a constant angular speed ω. What is the value of angle θ, when the bead is in dynamic equilibrium ?
View Solution
Knowledge Check
A ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png) Ag√3B2g√3rC√3grDgr
Ag√3B2g√3rC√3grDgrA thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is
 Apω2r2/2Bpω2r2Cpω2r2/3DNone
Apω2r2/2Bpω2r2Cpω2r2/3DNoneA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then is equal to:
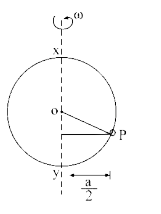 A2gaBg2aC2ga√3Dg√32a
A2gaBg2aC2ga√3Dg√32a
A wire of resistance 0.5ωm−1 is bent into a circle of radius 1m. The same wire is connected across a diameter AB as shown in fig. The equivalent resistance is
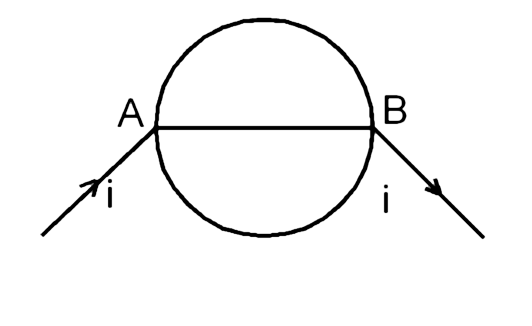
View SolutionTwo particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
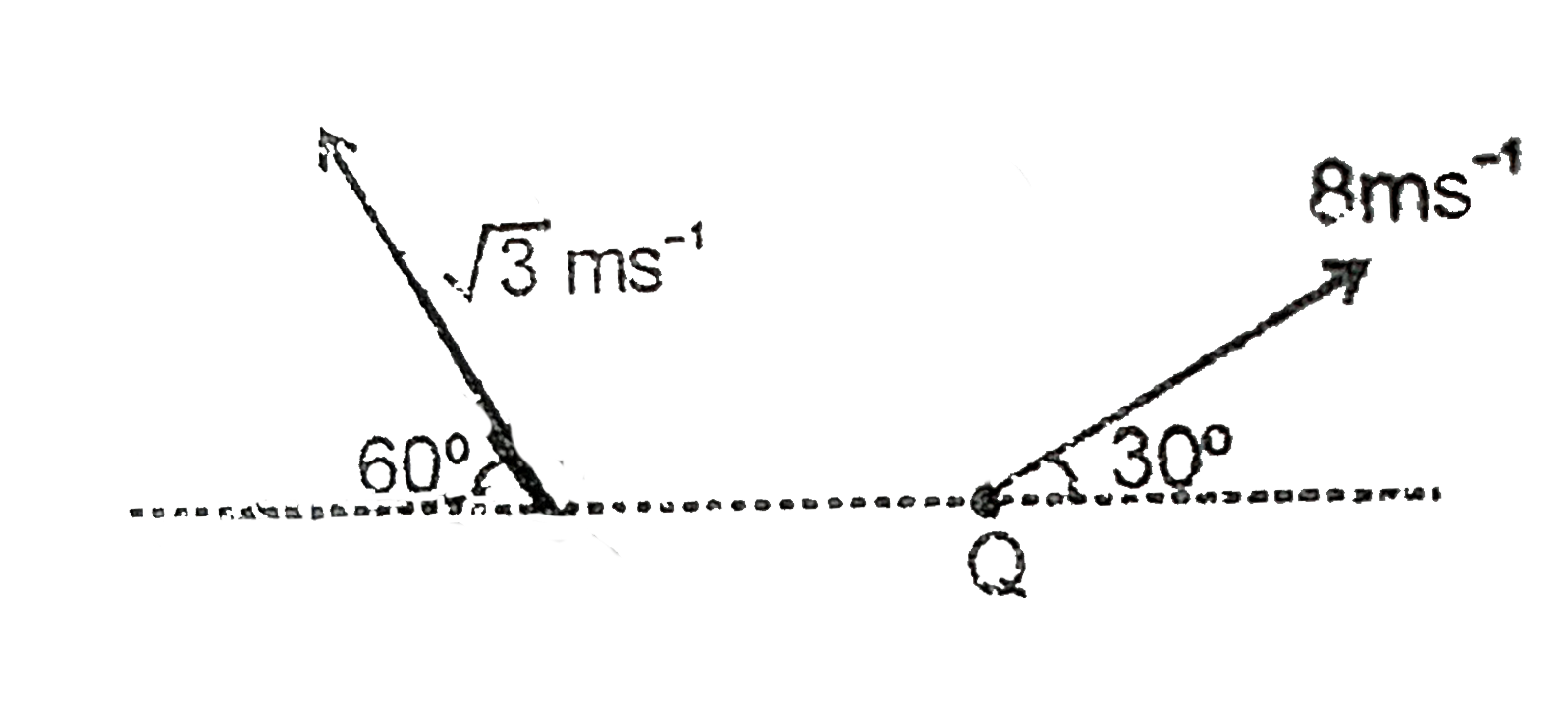
View SolutionA small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius a√32 is :

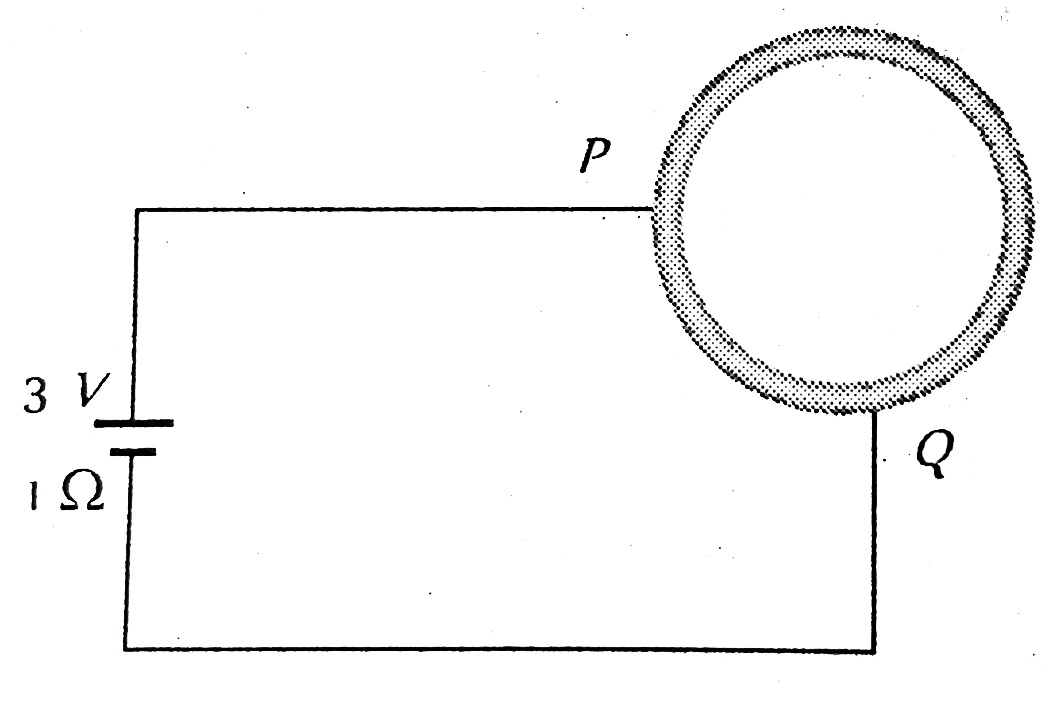
View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are
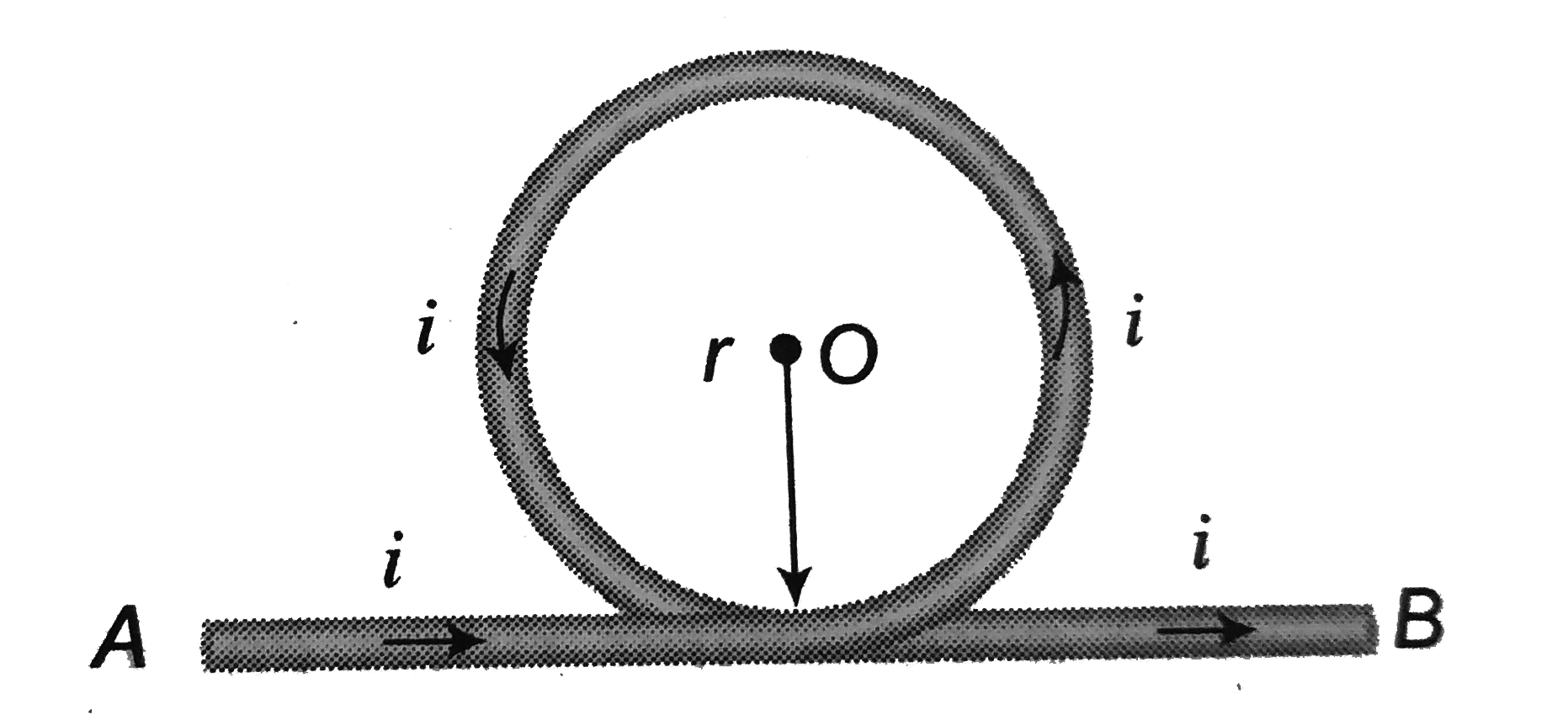
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
View Solution

