A solid sphere with angular velocity ω0 is dropped on a rough surface with coefficient of frication 'μ' froma height 'h'. If the collision with ground is perfectly inelastic if the velocity of centre of mass just after the impact is μ√xgh3 then value of x would be :
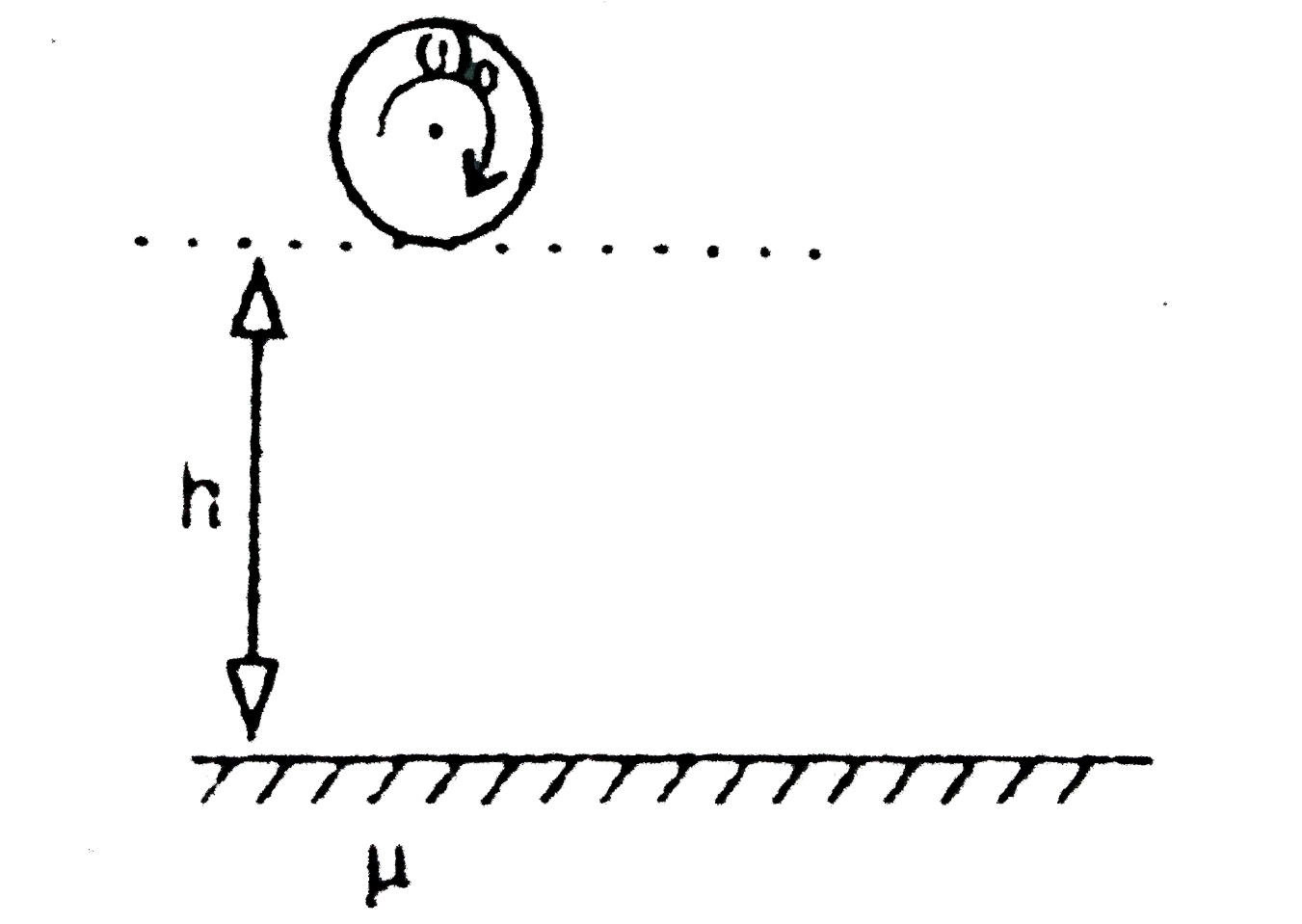
The correct Answer is:6
The collision is perfectly inelastic
Hence , ∫Ndt=m√2gh
and the linear impulse
∫μNdt=mv
μm√2gh=mv
v=μ√2gh
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Physics
775 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in m/s) of the sphere in horizontal direction immediately after the impact (given: Rω=5).
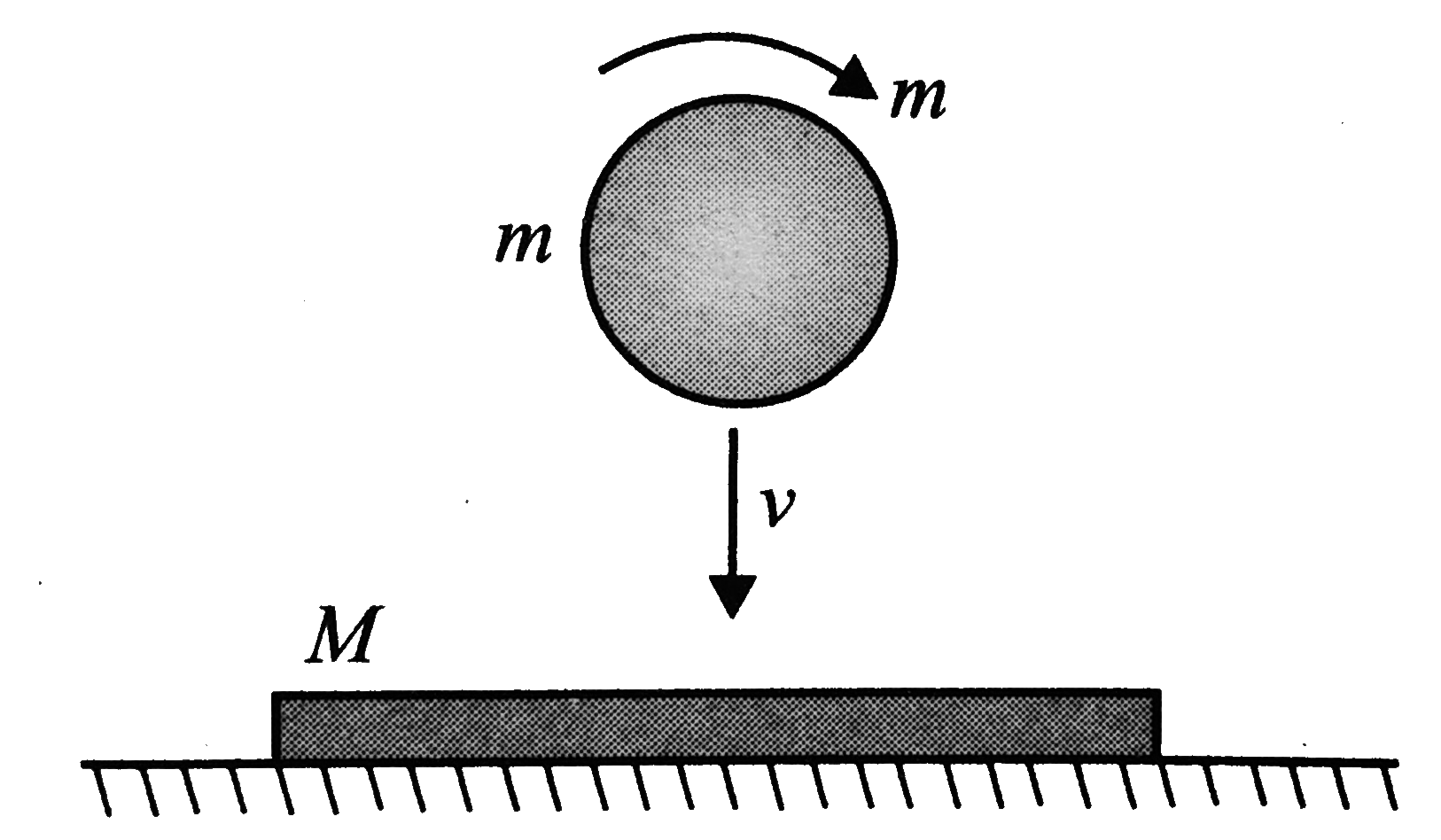
View SolutionA solid ball of mass m and radius R spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ ) and smooth lower surface. Immediately after collision, the normal component of velocity of the ball becomes half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given :Rω=5 ).

View Solution
Knowledge Check
A hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
Arω02Brω0Crω04Drω03A solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of v)Bmust be backward (opposite to v)Ccannot be zeroDnone of the aboveA hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
Arω04Brω03Crω02Drω0
A body of mass m is dropped from a height of h. Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h2. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View Solution
A solid sphere of mass 10 kg is placed on a rough surface having coefficient of friction μ=0.1A constant force F=7N is applied along a line passing through the centre of the sphere as shown in the figure. The value of frictional force on the sphere is
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time v0>ω0R)

View Solution