A solid ball of mass $m$ and radius $r$ spinning with angular velocity $ω$ falls on a horizontal slab of mass $M$ with rough upper surface (coefficient of friction $μ$ ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in $m / s$ ) of the sphere in horizontal direction immediately after the impact (given: $R ω = 5$ ).

Text Solution

Verified by Experts

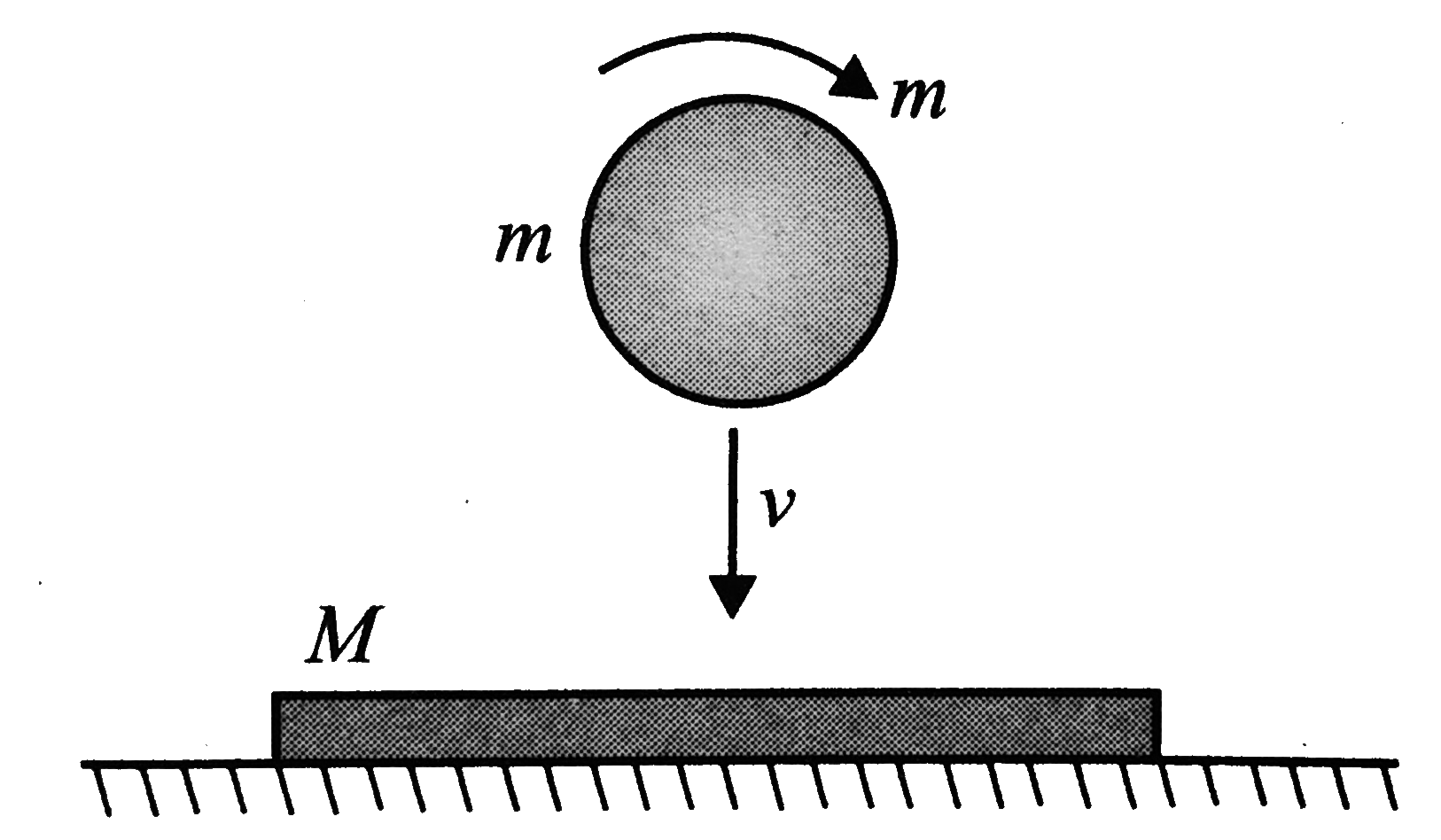
The correct Answer is:2

A ring of radius $R$ is first rotated with an angular velocity $ω$ and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is $μ$ . Time after which its angular speed is reduced to half is
A $\frac{ω_{0} μ R}{2 g}$
B $\frac{ω_{0} g}{2 μ R}$
C $\frac{2 ω_{0} R}{μ g}$
D $\frac{ω_{0} R}{2 μ g}$
A ball of mass $m$ is projected with a velocity $' u'$ at angle $θ$ with the horizontal. It collides with a smooth box of mass $' M'$ at its highest position. If the co-efficient of restitution is $' e'$ .

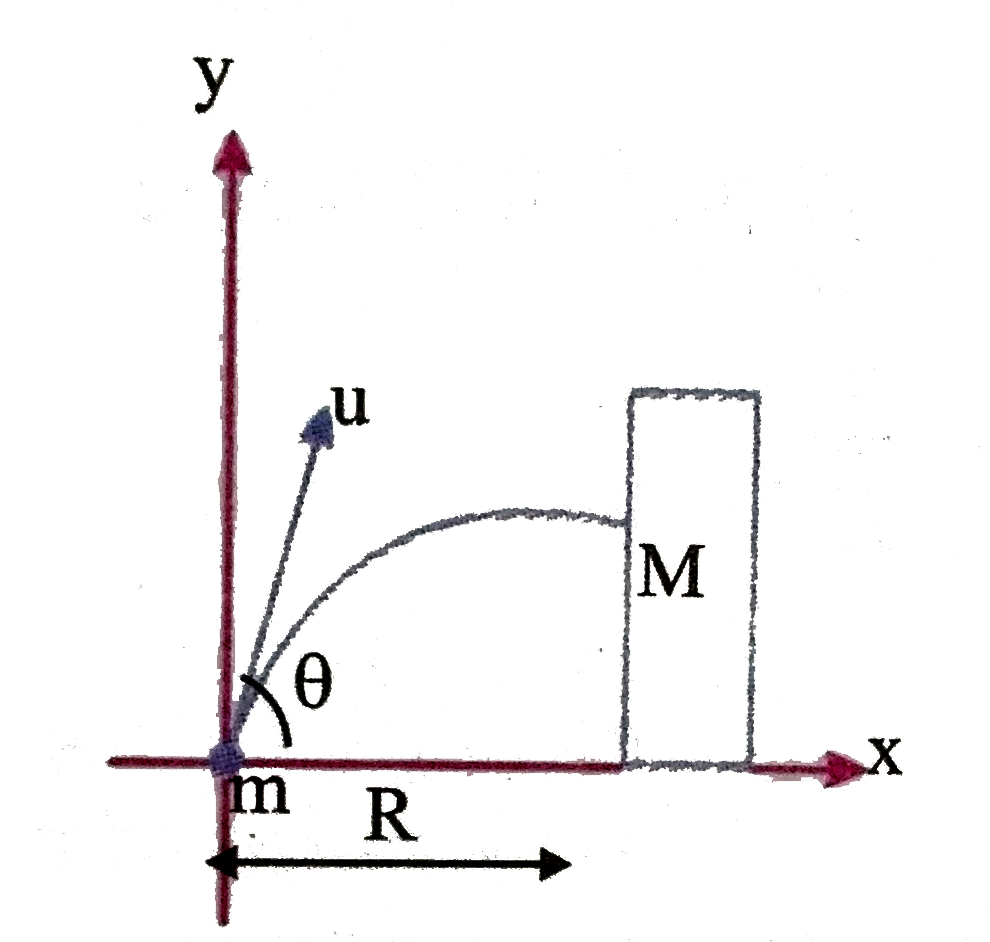
FInd the velocity of the ball after collision
A $(\frac{m - e M}{M + m}) u cos θ$
B $(\frac{M - e m}{M + m}) u cos θ$
C $(\frac{m + e M}{M + m}) u sin θ$
D $(\frac{m - e M}{M + m}) u sin θ$
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is $v_{1}$ and velocity of second ball after collision is $v_{2}$ then
A $v_{1} = \frac{(1 - e) u}{2}, v_{2} = \frac{(1 + e) u}{2}$
B $v_{1} = \frac{(1 + e) u}{2}, v_{2} = \frac{(1 - e) u}{2}$
C $v_{1} = \frac{u}{2}, v_{2} = - \frac{u}{2}$
D $v_{1} = (1 + e) u, v_{2} = (1 - e) u$