A gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:
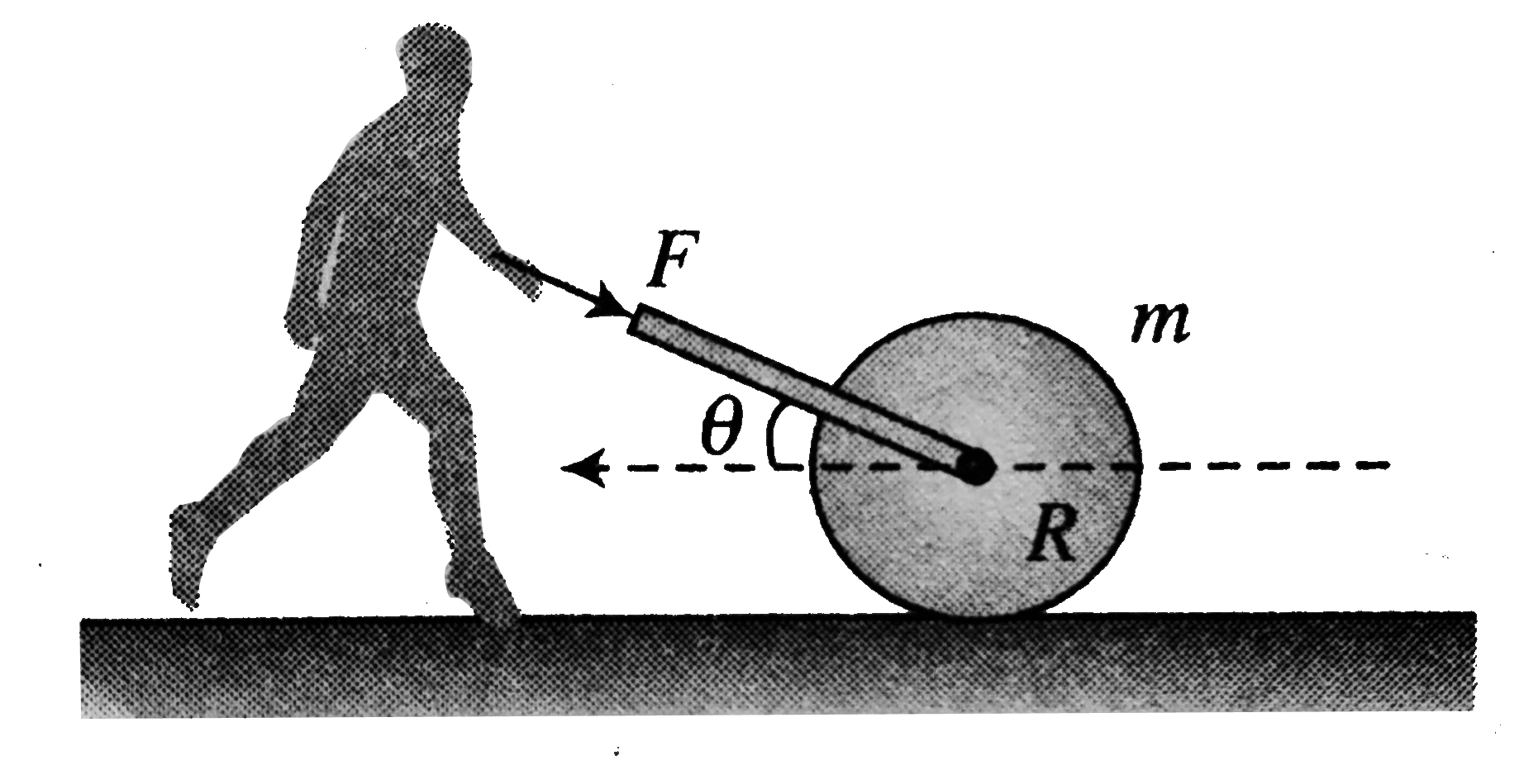
friction between the grasscutter (assumed as a disc) and ground.
Fsinθ3
Fcosθ3
2F3
2Fcosθ3
The correct Answer is:B
Fcosθ−f=ma …………i
fR=12mR2α⇒fR=12mR2aR
⇒f=ma2………ii
From i and ii
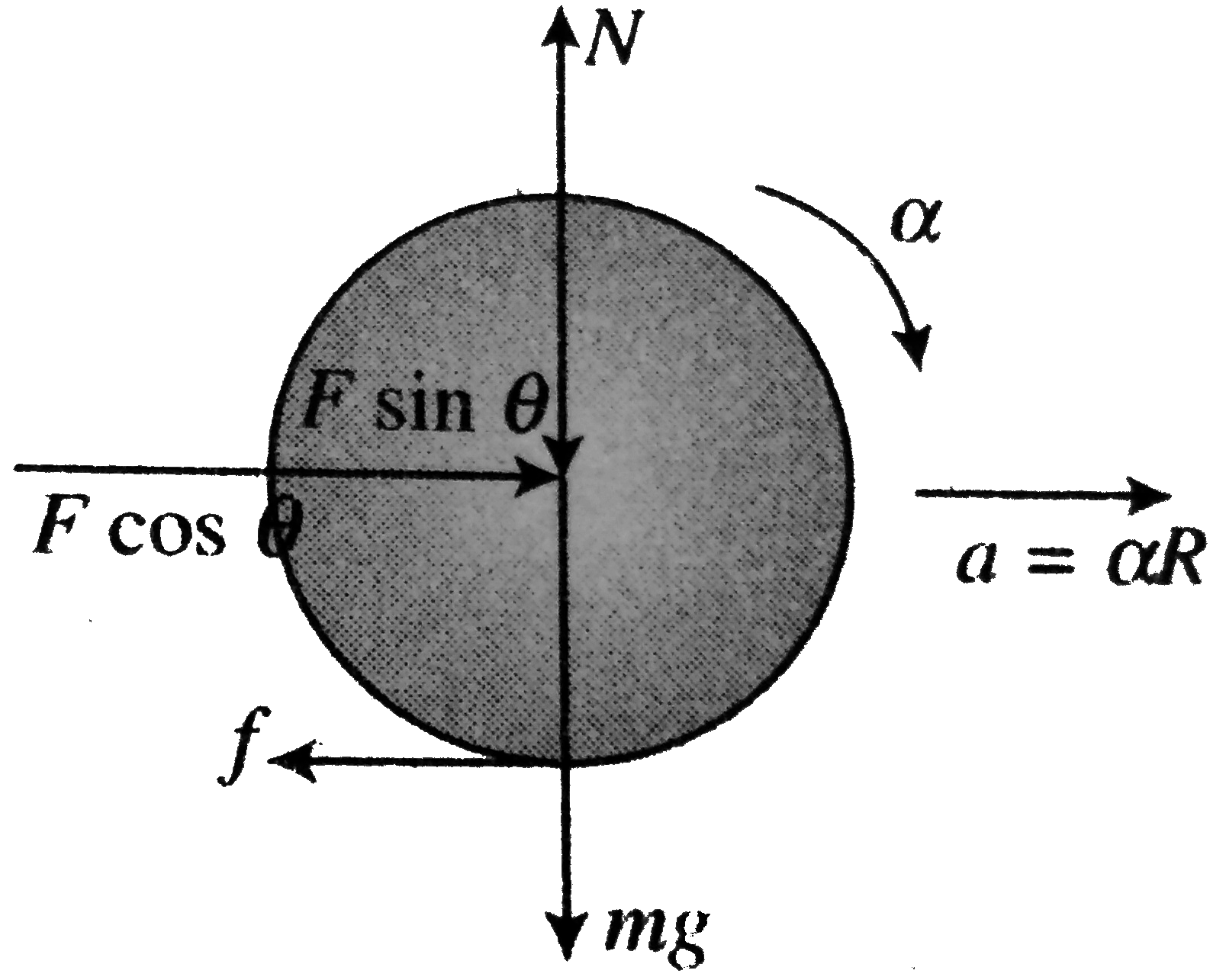
f=Fcosθ3
Now a=2fm=2Fcosθ3m
f≤f1⇒Fcosθ3≤μN
⇒Foscosθ3≤μ(mg+Fsinθ)⇒F≤3μmgcosθ−3μsinθ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A truck of mass M has 4 wheels. The surface area of the metal disc in each wheel is A. When brakes are applied the brake shoe in each wheel rubs against the metal disc. This produces heat. We will assume that this heat is used to heat the disc in the wheel only. Each disc has mass m and is made of material of specific heat capacity s. One day the truck was going downhill on a road inclined at angle θ to the horizontal. To maintain a constant speed v the driver had to apply brakes. The only other dissipative force, apart from the brake force, on the truck is the air resistance force that is equal to F. Assume no heating of discs due to air friction.
(a) Find the initial rate of rise of temperature of each metal disc after the brakes are applied.
(b) Find the final temperature (T) of the disc assuming that it is a black body and it loses heat only through radia- tion. Take the atmospheric temperature to be T0
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View Solution
Knowledge Check
A gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:
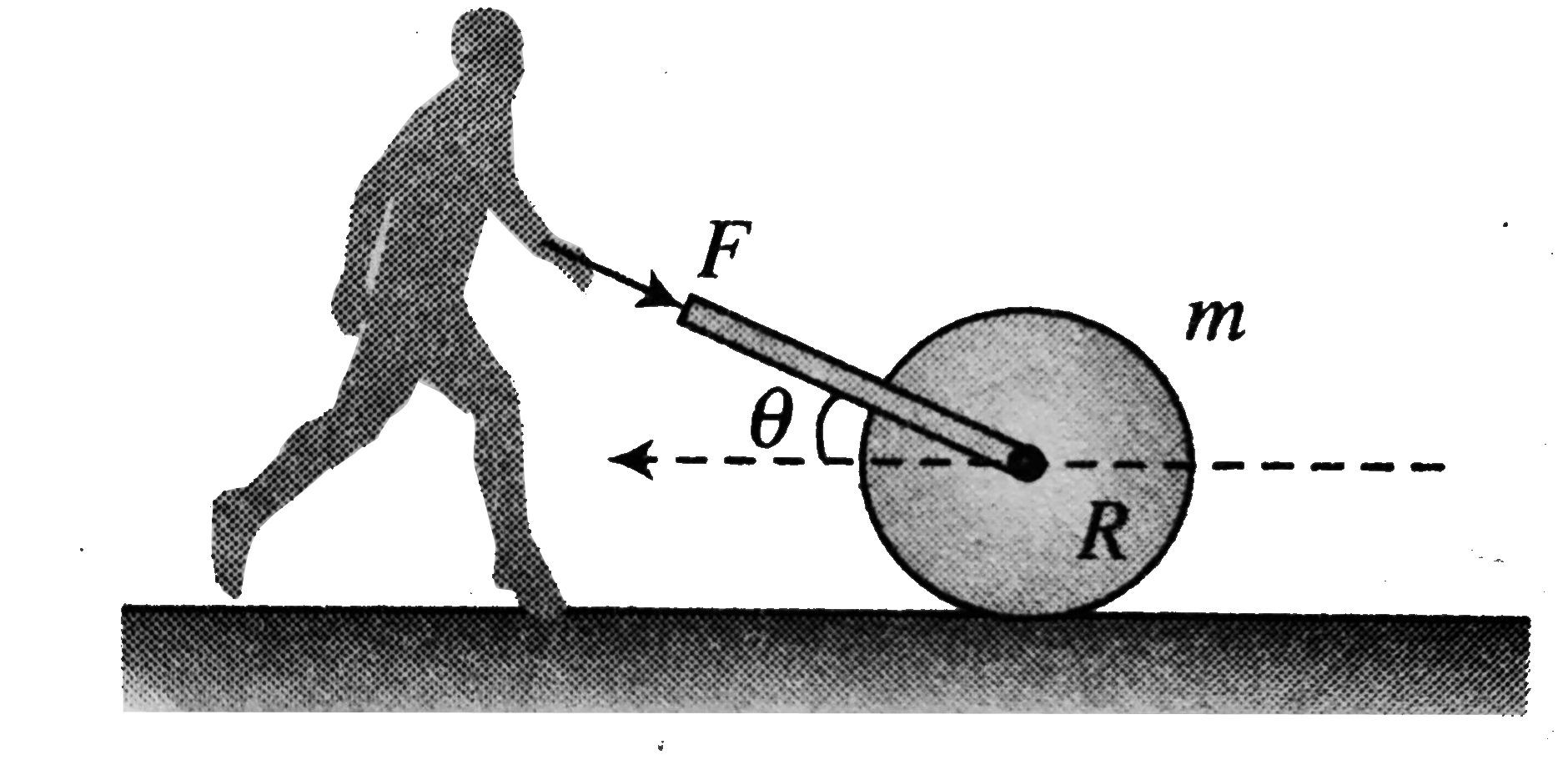
Acceleration of CM of the roller (disc). Assume that the mass of the disc is m and neglect the mass of the connecting rod.A2Fcosθ3mBFsinθ3mC2Fsinθ3mDFcosθ3mA gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:
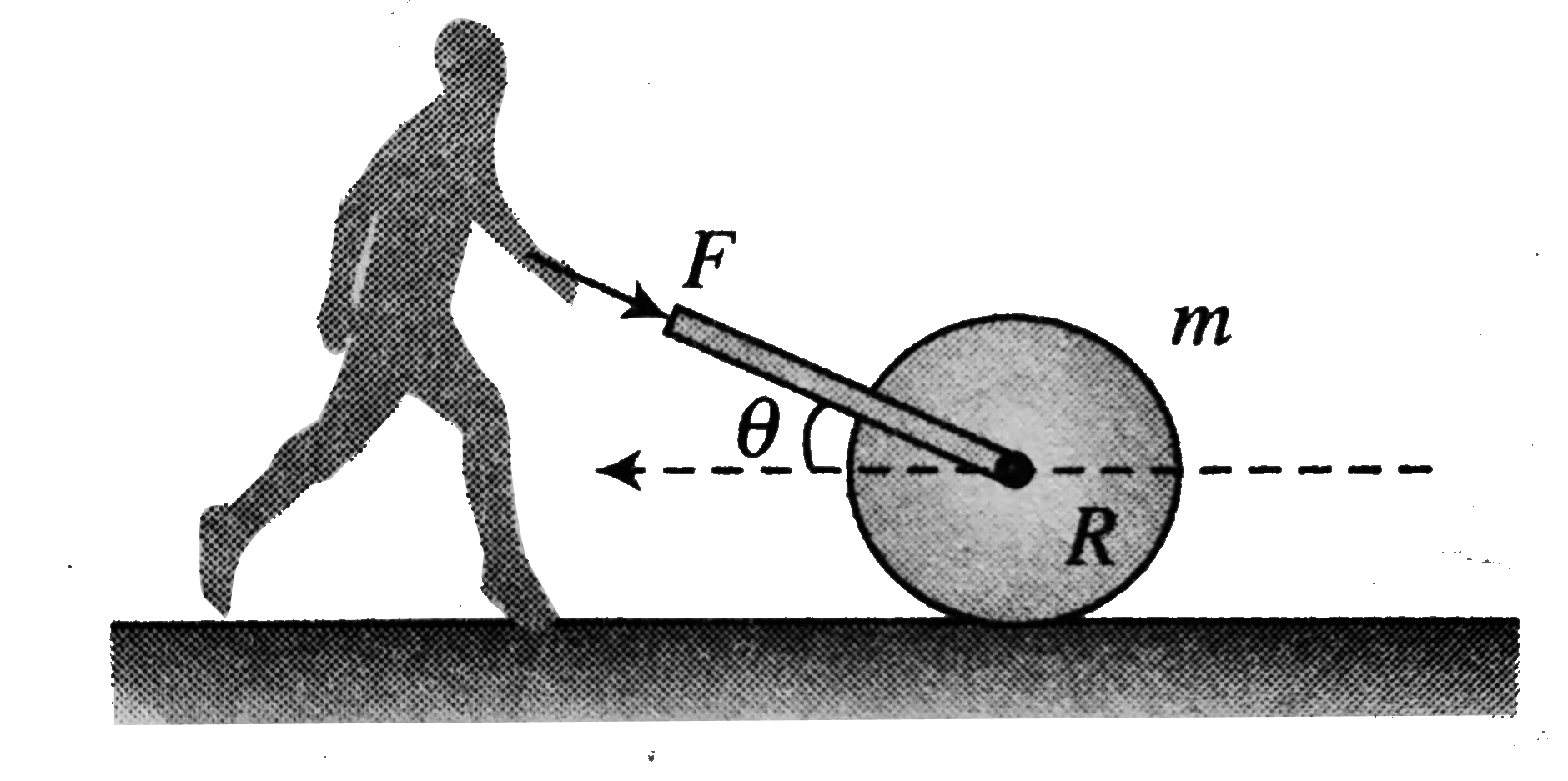
Maximum force F for no relative slidng if th coeficient of friction between the roller and ground is μAμmgcosθcosθ+3μsinθBμmgsinθcosθ+3μsinθC3μmgcosθ−3μsinθD3μmgcosθ+3μsinθ
When F = 2 N , the frictional force between 5 kg block and ground is :A2NB0C8 ND10 N
A stick o fmas density λ=8kg/m rests on a disc of radius R=20cm as shown in the figure. The stick makes an angle θ=37∘ with the horizontal and is tangent to the disc at its upper end. Friction exists at all point of contact and assume that it is large enough to keep the system at rest. Find the friction force (in Newton) between the ground and the disc. (take g=10m/s2)

View SolutionIn previous question, if we pull the block by the force F making an angle theta and the block remains stationary, the value of friction force is.

View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
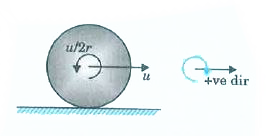
What will be the speed of sphere when it starts pure rolling?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
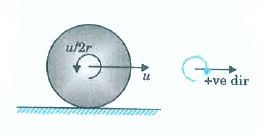
At what time sphere starts pure rolling?
View Solution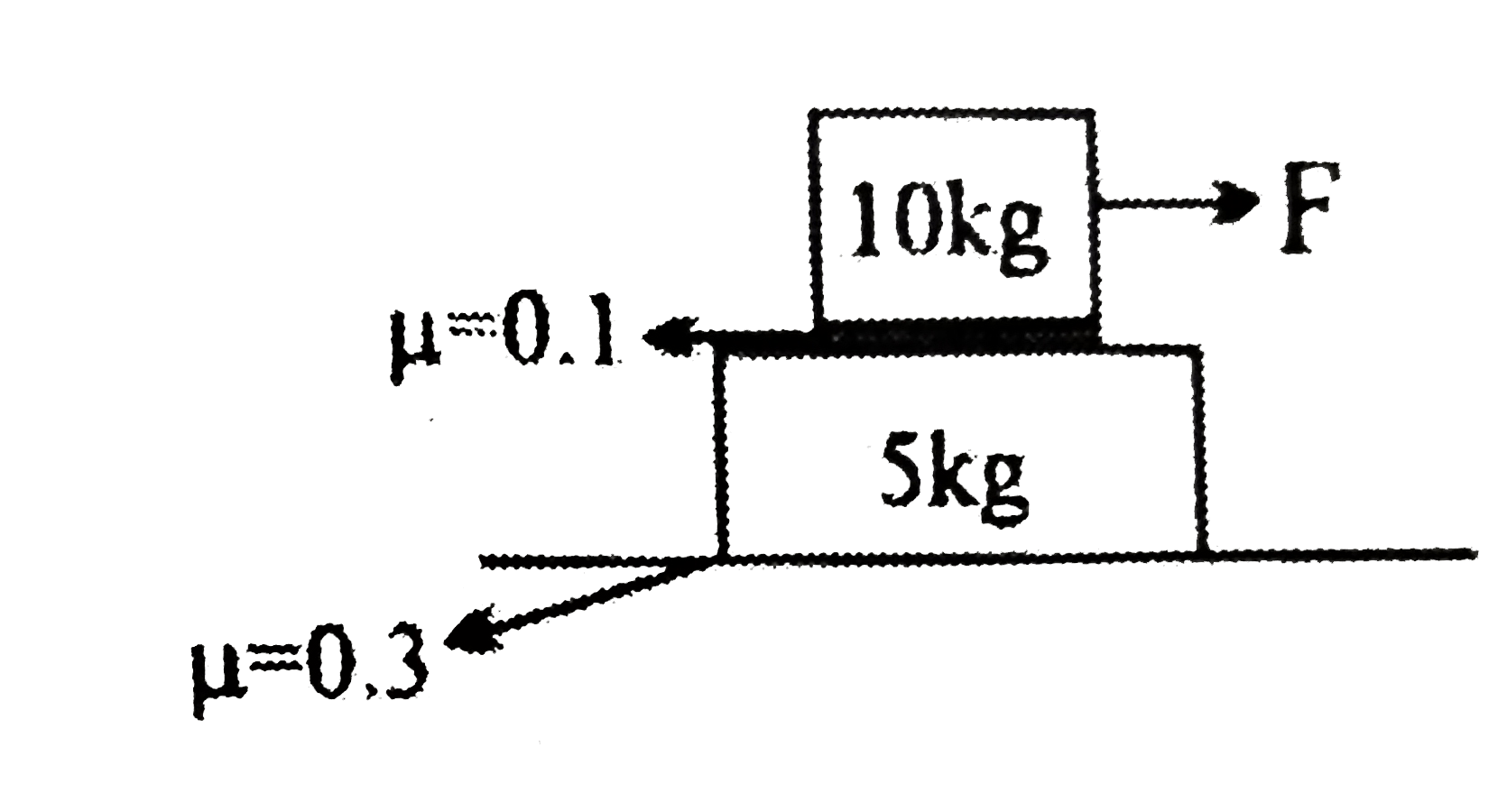
When F = 2N, the frictional force between 5 kg block and ground is
View Solution
