A unifrom rod AB of length 4m and mass 12kg is thrown such that just after the projection the centre of mass of the rod moves vertically upwards with a velocity 10m/s and at the same time its is rotating with an angular velocity π2rad/sec about a horizontal axis passing through its mid point. Just after the rod is thrown it is horizontal and is as shown in the figure. Find the acceleration (in m/sec2) of the point A in m/s2 when the centre of mass is at the highest point. (Take =10m/s2 and π2=10)

The correct Answer is:5
Time in which C.M. reaches its highest point =1sec. (from v=u+at, putting v=0,u=+10,a=10m/sec2) after projection angular velocity will not change as the torque of external forces is zero.
In 1sec., the rod will rotate by an angle =ωt=πt2×t rad.
The rod will be vertical with point A at the lowest point.
∴aA=g−ω2L/2=10−π244×2=5m/sec2.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Physics
775 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AYA uniform metal rod of length 1 and mass m is rotating with an angular velocity of magnitude o about an axis passing through its centre and perpendicular to the rod. If the temperature of the rod increases by T∘C , then change in its magnitude of angular velocity varies directly with
A1ωB√ωCωDω2
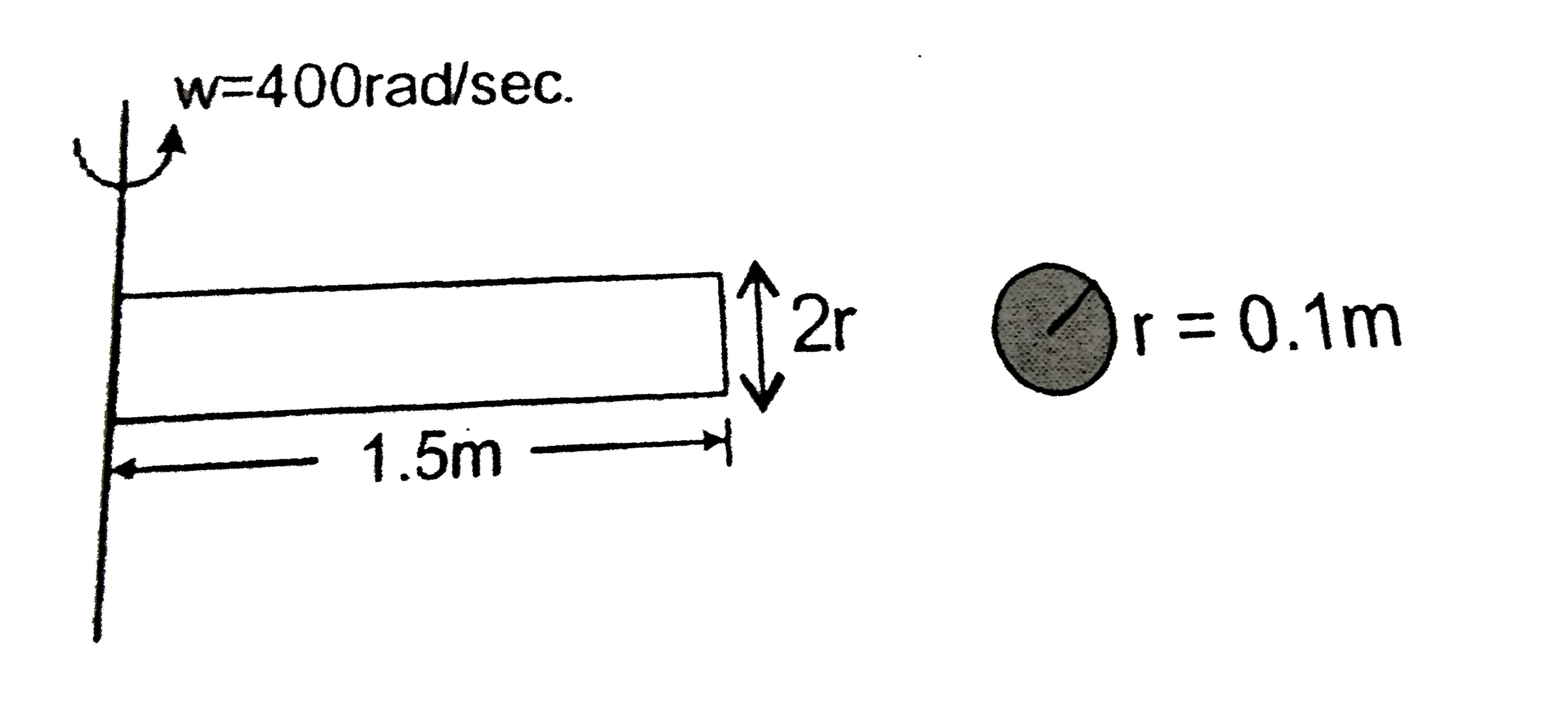
A rod of 1.5m length and uniform density 104kg/m3 is rotating at an angular velocity 400rad/sec about its one end in a horizontal plane. Find out elongation in rod.
Given y=2×1011N/m2
View SolutionA rod of length l and total charge 'q' which is uniformly distributed is rotating with angular velocity ω about an axis passing through the centre of rod and perpendicular to rod. Find the magnitude of magnetic dipole moment (in Amp. m2) of rod. If q=4C,ω=3rad/s and l=2m
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA thin rod AB of mass M and length L is rotating with angular speed ω0 about vertically axis passing through its ends B on a horizontal smooth table as shown. If at some instant the hinge at end B of rod is opened then which of the following statemtents is / are correct about motion of rod?

View Solution
