A uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. The time period of small oscillations of remaining portion about O is -

3π√Rg
π√13Rg
2π√39R16g
2π√7R6g
The correct Answer is:B
A uniform …………
T=2π√Imgycm
I=MR22−(12M4(R2)2+M4(R2)2)=13MR232
ycm=R6
T=2π√134Rg
Similar Questions
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionFrom a circular disc of radius R, another disc of diameter R is removed. Locate c.m. of the remaining portion.

View Solution
Knowledge Check
A uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. Then choose the correct option(s)
 ATime period of small oscillations of remaining portion about O is π√13RgBTime period of small oscillations of remaining portion about O is 2π√13RgCThe centre of mass of the remaining disc is at a distance of R6 from O.DThe centre of mass of the remaining disc is at a distance of R8 from O.
ATime period of small oscillations of remaining portion about O is π√13RgBTime period of small oscillations of remaining portion about O is 2π√13RgCThe centre of mass of the remaining disc is at a distance of R6 from O.DThe centre of mass of the remaining disc is at a distance of R8 from O.A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
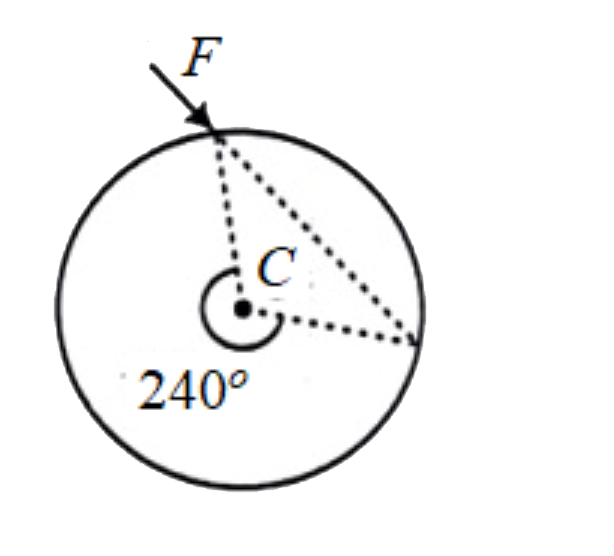 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
A2π√RgB2π√2RgC2π√2π3gD2π√3R2g
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View SolutionA uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View Solution
