In YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
_E01_031_O01.png)
_E01_031_O02.png)
_E01_031_O03.png)
_E01_031_O04.png)
The correct Answer is:C
_E01_031_S01.png)
When μ=1 i.e., no change in path difference due to optical path difference so that mid point of the screen is again the central bright fringe.
But when μ>1 the central bright will shift according Dd(μ−1)t
As μ increases, CBF will shift upwards from midpoint i.e., at mid point. Less bright fringe appears and when the shifts is equal to value of fringe width, the dark (zero intensity) will appear.
or Intensity variation
O≡central bright fringe
y≡distance from 'O' screen
_E01_031_S02.png)
* When μ increases, the fringe patterns shift towards the slit when introduced shift D(μ−1)t from the above two fact variation in I with μ is
Topper's Solved these Questions
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Brain Teasures)
Explore 22 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 3 (Miscellaneous type Questions)
Explore 27 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Example 15
Explore 1 Video
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
A plate of thickness t made of material of refractive index μ is placed in front of one of the slits in a double slit experiment . What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ?
View SolutionMonochromatic light of lamba=5000Å is incident on two slits separately by a distance of 5×10−4m. The interference patteren is seen on a screen placed at a distance of 1m form the slits. A thing glass plate of thicknes 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the centre of the screen if the density there is I0 in the absence of the plate. Also find the lateral shift of the central maximum. '
View Solution
Knowledge Check
In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)In a regular YDSE, when thin film of refractive index mu is placed in front of the upper slit then it is observed that the intensity at the central point becomes half of the original intensity. It is also observed that the initial 3^(rd) maxima is now below the central point and the initial 4th minima is above the central point. Now, a film of refractive index μ1 and thickness same as the above film. is put in the front of the lower slit also. It is observed that whole fringe pattern shifts by one fringe width. What is the value of μ1 ?
A(4μ+9)/12B(4μ+9)/13C(4μ+9)/11DNoneIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
Aβ(μ−1)t2λBβ(μ−1)tλCβ(μ−1)t3λDβ(μ−1)t4λ
A monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the centre of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through centre.
View SolutionIn Young's experiment, if a slab of mica of refractive index μ and thickness of t is introduced in the path of light from one of the slits, then number of fringes formed on the screen will –
View SolutionMinimum thickness of a mica sheet having μ=32 which should be placed in front of one of the slits in YDSE is required to reduce the intensity at the centre of screen to half of maximum intensity is
View SolutionThe slits in a double-slit interference experiment are illuminated by orange light (λ=60nm). A thin transparent plastic of thickness t is placed in front of one of the slits. The nunber of fringes shifting on screen is plotted versus the refractive index μ of the plastic in graph shown in figure. The value of t is
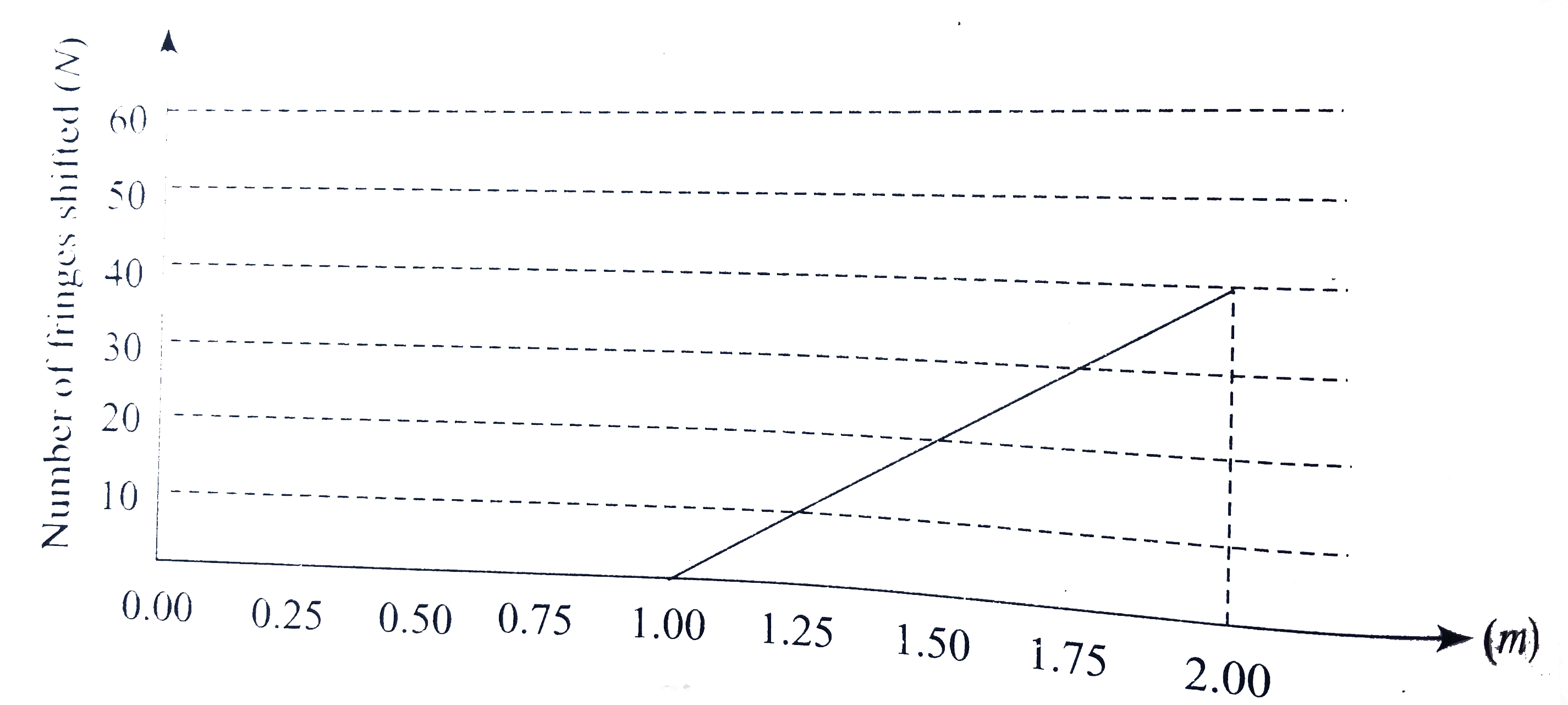
View SolutionIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
View Solution

