_S01_033_Q01.png)
In a typical young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity v=1 mm per second towards the screen, then the instantaneous velocity of central maxima is given as α×10−βcm/s upward in scientific notation find the value of α+β
_S01_033_S01.png)
The central maxima dyD=√d2+x2−x=x[1+d22x2]−x=d22x
y=Dd2x⇒dydt=−Dd2x2(dxdt)=(1×0.012×0.5×0.5)×(0.001)=0.02mm/s
⇒y=2×10−3cm/s⇒α+β=5
Topper's Solved these Questions
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 1 (Check your Grasp)
Explore 75 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Brain Teasures)
Explore 22 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Example 14
Explore 1 Video
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
In the Young's double slit experiment a point source of λ=5000Å is placed slightly off the central axis as shown in the figure-6.127.

(a) Find the nature and order of the interference at the point P.
(b) Find the nature and other of the interference at O.
(c ) Where should we place a film of refractive index μ=1.5 and what should be its thickness so that maxima of zero order is obtained at O.
View SolutionIn Young's double slit experiment, the distance between two coherent sources is 1 mm and the distance between the slits and the screen is 1 m. If the 10th dark fringe is at a distance of 4.75 mm from the central bright fringe, calculate
the wavelength of light used and
View Solution
Knowledge Check
In Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,where I0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
 Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)A monochromatic beam of light falls on Young's double slit experiment apparatus as shown in figure. A thin sheet of glass is inserted in front of lower slit S2(λ=600nm is wavelength of source)

The phase difference between central masxima and 5th minima isAπ6B9πC3π2D8π±π6In a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:

If a liquid is filled between the slit and the source S, what is the phase difference?A2πλ[n√d2+x20−x0−d22D]B2πλ[n√d2+x20−x0+d22D]C2πλ[n√d2+x20+x0+d22D]D2πλ[n√d2−x20−x0−d22D]
Light of wavelength λ from a small 0.5mW He-Ne laser source is used in the school laboratory to shine on perfectly absorbing surface of a spacecraft of mass 1000kg. The tịne needed' for the spacecraft to reachi a velocity of 1kms from rest is given by α×10β(s) in scientific notation. Find the value of (β−r2α).
View SolutionIn a Young's double slit experiment, slits are seperated by a distance d and screen is at distance D, (D>>d) from slit plane. If light source of wavelength λ(λ<<d) is used. The minimum distance from central point on the screen where intensity is one fourth of the maximum is Dλnd. Find the value of n.
View SolutionIn a Young’s double slit experiment a monochromatic light whose wavelength is l strikes on the slits, separated by distance d, as shown in the figure. Refractive index of the medium between slits and screen varies with time t as n = n0 + kt. Here n0 and k are positive constants. Position of any point P on screen is measure by its y-coordinate as shown.
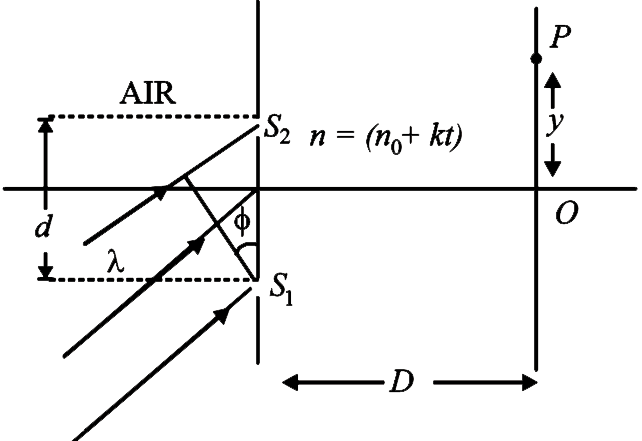
The velocity of central maxima at any time t as a function of time t is
View SolutionIn a Young’s double slit experiment a monochromatic light whose wavelength is l strikes on the slits, separated by distance d, as shown in the figure. Refractive index of the medium between slits and screen varies with time t as n = n0 + kt. Here n0 and k are positive constants. Position of any point P on screen is measure by its y-coordinate as shown.
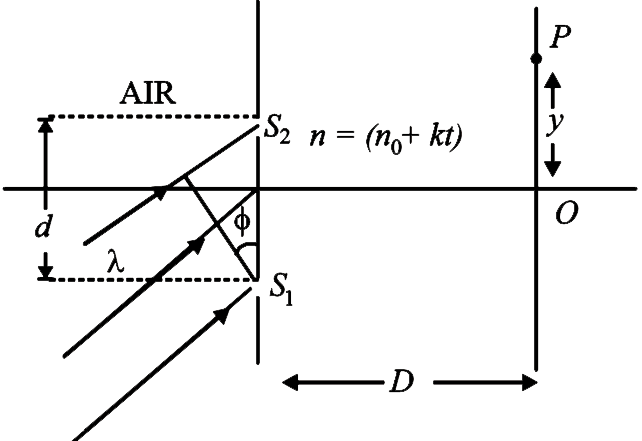
The y co-ordinate of central maxima at any time t is
View SolutionIn a Young’s double slit experiment a monochromatic light whose wavelength is l strikes on the slits, separated by distance d, as shown in the figure. Refractive index of the medium between slits and screen varies with time t as n = n0 + kt. Here n0 and k are positive constants. Position of any point P on screen is measure by its y-coordinate as shown.
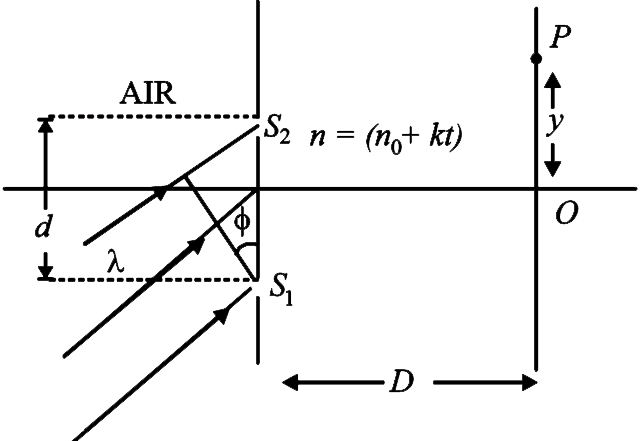
If a glass plate of small thickness b is placed in front of S1. How should its refractive index vary with time so that central maxima is formed at O.
View Solution

