_E01_036_Q01.png)
Two point source separated by emit light of wavelength in phase A cicular wire of radius is placed aournd the source as shown in figure.
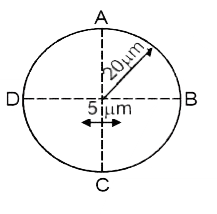
Points A and B are dark and points C and D are bright.
Point A and B are bright and point C and D are dark
Point A and C are dark and points B and D are bright.
Points A and C are bright and points B and D are dark.
The correct Answer is:D
Path difference for points A & C is O so constructive interference take place.
Path difference for B & D
So distructive interference take place.
Topper's Solved these Questions
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Brain Teasures)
Explore 22 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 3 (Miscellaneous type Questions)
Explore 27 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Example 15
Explore 1 Video
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
Two point source separated by d=5μm emit light of wavelength λ=2μm in phase. A circular wire of radius 20μm is placed around the source as shown in figure. Which point are dark and bright.
View SolutionTwo coherent point source S1 and S2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at 'P' due to interference on a screen placed at distance 'D' from S1(D>>λ), then OP is

1) √3D,2)1.5D,3)√2D,4)2D
View Solution
Knowledge Check
Two point sources separated by 2.0 m are radiating in phase with λ=0.50m. A detector moves in a circular path around the two sources in a plane containing them. How many maxima are detected?
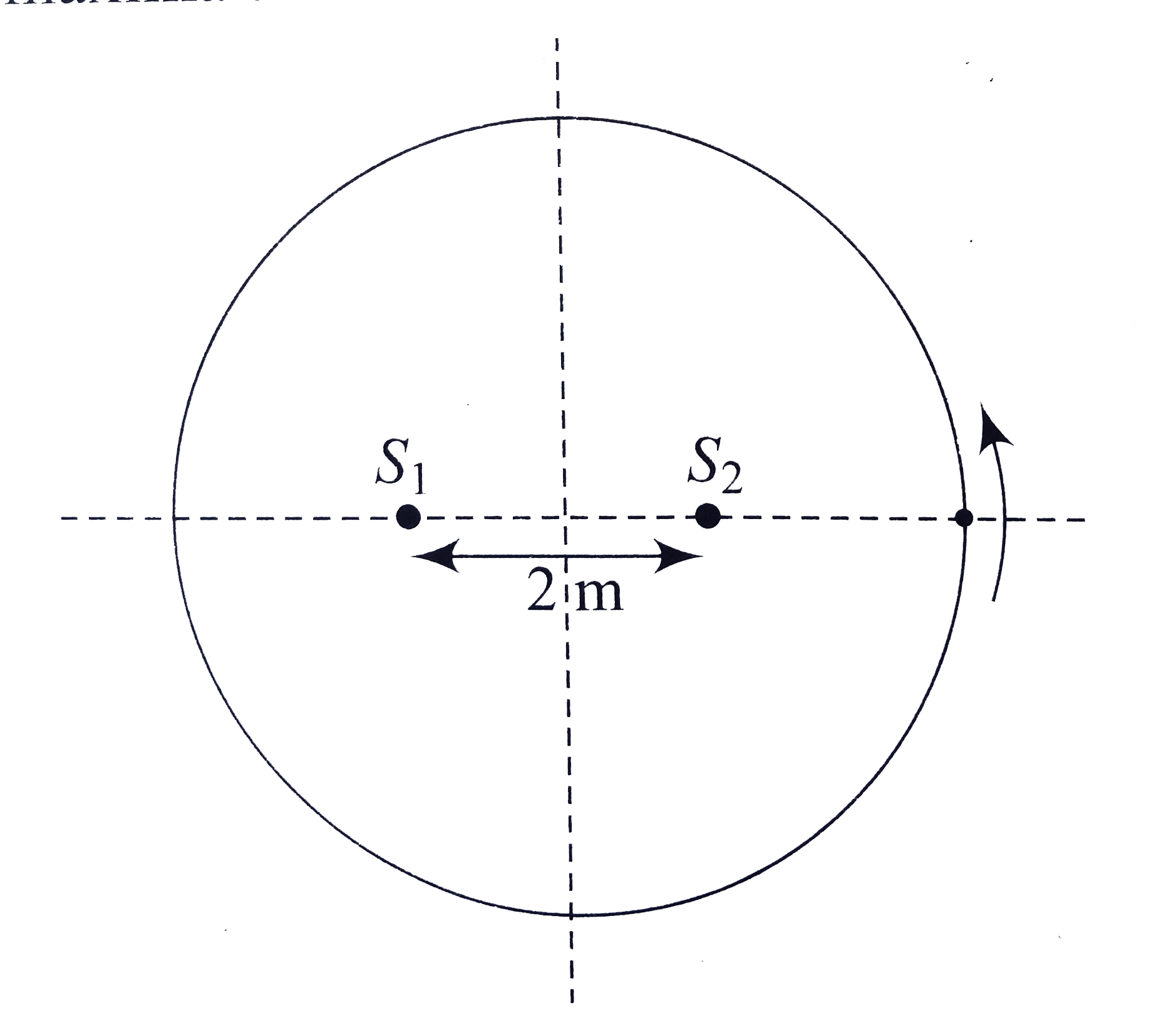 A16B20C24D32
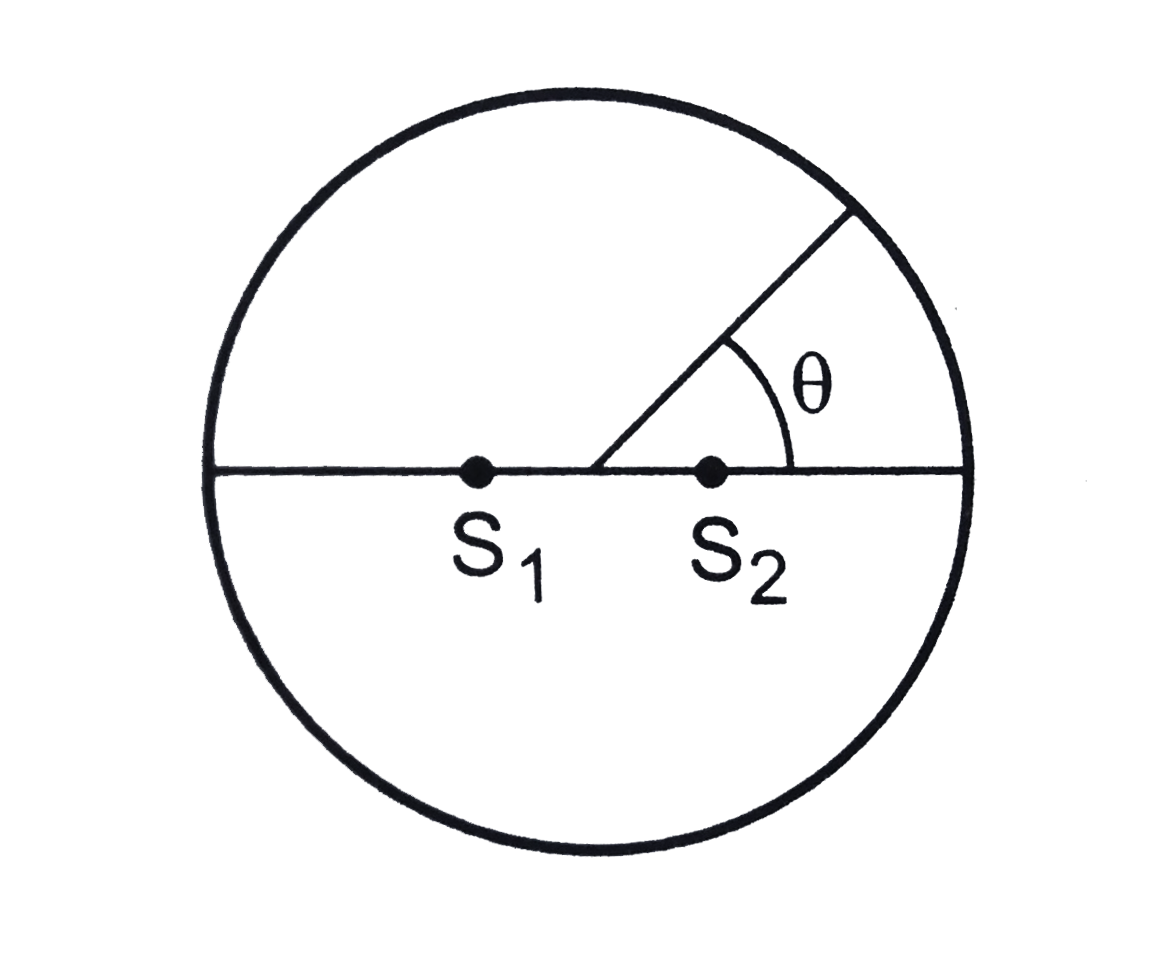
A16B20C24D32Two coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as
 Asin−1(nλ)dBcos−1(4λd)Ctan−1(d)4λDcos−1(λ)4d
Asin−1(nλ)dBcos−1(4λd)Ctan−1(d)4λDcos−1(λ)4dTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
A(a) Their phase differences remain constantB(b) Their phases are distributed randomlyC(c) Their light intensities remain constantD(d) Their light intensities change randomly
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O

View SolutionFigure shows two coherent sources S1andS2which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire at large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2, is at the centre of the wire. Find the angular positions 0 on the wire for which constructive interference takes place.
View SolutionA mono chromatic light source of wave length I is placed at a distance R from the mirror as shown and a spherical screen of radius R is at a distance R from the source as shown in the figure and point P is on the sphere nearest to the source.It R is two times the wave length (R=2l) then f'+(p)
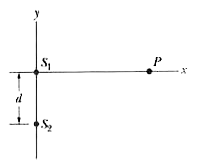
View SolutionFigure shows two point sources S1 and S2 that emit sound of wavelength λ = 3.00 m. The emissions are isotropic and in phase, and the separation between the sources is d = 16.0 m. At any point P on the x axis, the wave from S1 and the wave from S2 interfere. When P is very far away (x≈0) , what are (a) the phase difference between the arriving waves from S1 and S2 and (b) the type of interference they produce? Now move point P along the x axis toward S1. (c ) Does the phase difference between the waves increase or decrease? At what distance x do the waves have a phase difference of (d) 0.50λ,(e)1.00λ, and (f) 1.50λ?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View Solution

