In a YDSE with two identical slits, when the upper slit is covered with a thin, perfectly tranparent sheet of mica, the intensity at the centre of screen reduces ro 75% of the initial value. The second minima is observed to above this point and third maxima below it. which of the following can not be a possible value of phase difference caused by the mica sheet
π3
13π3
17π3
11π3
The correct Answer is:A
I'=34(4I)=3I
So 4I=I+I+2Icosϕ⇒cosϕ=12⇒ϕ=π3
But value should lie between 3π & 6π
So it cannot be π3
for second minima ϕ=3π
for third maxima ϕ=6π
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Brain Teasures)22videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 3 (Miscellaneous type Questions)27videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Example 151videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
In YDSE using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.5 and thickness 2 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the plane of slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the light.
View SolutionIn YDSE using monochromatic light the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the plane of slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the light.
View Solution
Knowledge Check
- Question 1 - Select One or More
In a YDSE with two identical slits, when the upper slit is covered with a thin, perfectly tranparent sheet of mica, the intensity at the centre of screen reduces ro 75% of the initial value second minima is observed to the above this point and third maxima below it which of the following can not be a possible value of phase difference caused by the mica sheet
Aπ3B13π3C5π3D11π3 - Question 2 - Select One
In a regular YDSE, when thin film of refractive index mu is placed in front of the upper slit then it is observed that the intensity at the central point becomes half of the original intensity. It is also observed that the initial 3^(rd) maxima is now below the central point and the initial 4th minima is above the central point. Now, a film of refractive index μ1 and thickness same as the above film. is put in the front of the lower slit also. It is observed that whole fringe pattern shifts by one fringe width. What is the value of μ1 ?
A(4μ+9)/12B(4μ+9)/13C(4μ+9)/11DNone - Question 3 - Select One
Young's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.

The phase difference at point P without inserting the slab isA3π/4Bπ/4Cπ/2Dπ/3
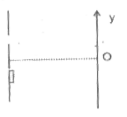
Young’s double slit experiment is done in a medium of refractive index 4/3. Light of 600 nm wavelength is falling on the slits having 0.45 pm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 pm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown.
(a) Find the location of central maxima (bright fringe with zero I t y path difference) on the y-axis.
(b) Find the light intensity at point O relative to the maximum fringe intensity.
(c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that from maxima exactly at point O[All wavelengths in this problem are for the given medium of refractive index 43. Ignore dispersions.]
 View Solution
View SolutionThe young's double slit experiment is done in a medium of refractive index 4/3.A light of 600nmwavelength is falling on the slits having 0.45 mm separation .The lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index1.5.the intereference pattern is observed ona screen placed 1.5m from the slits are shown
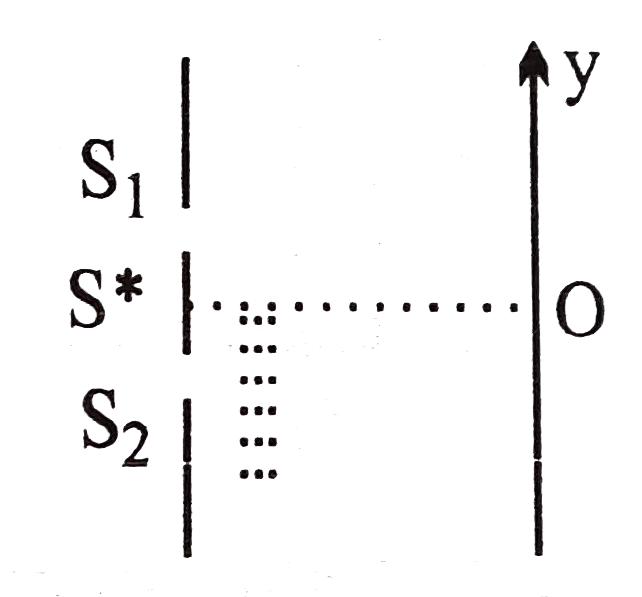
(a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis.
(b) Find the light intensity at point Orelative to the maximum fringe intensity.
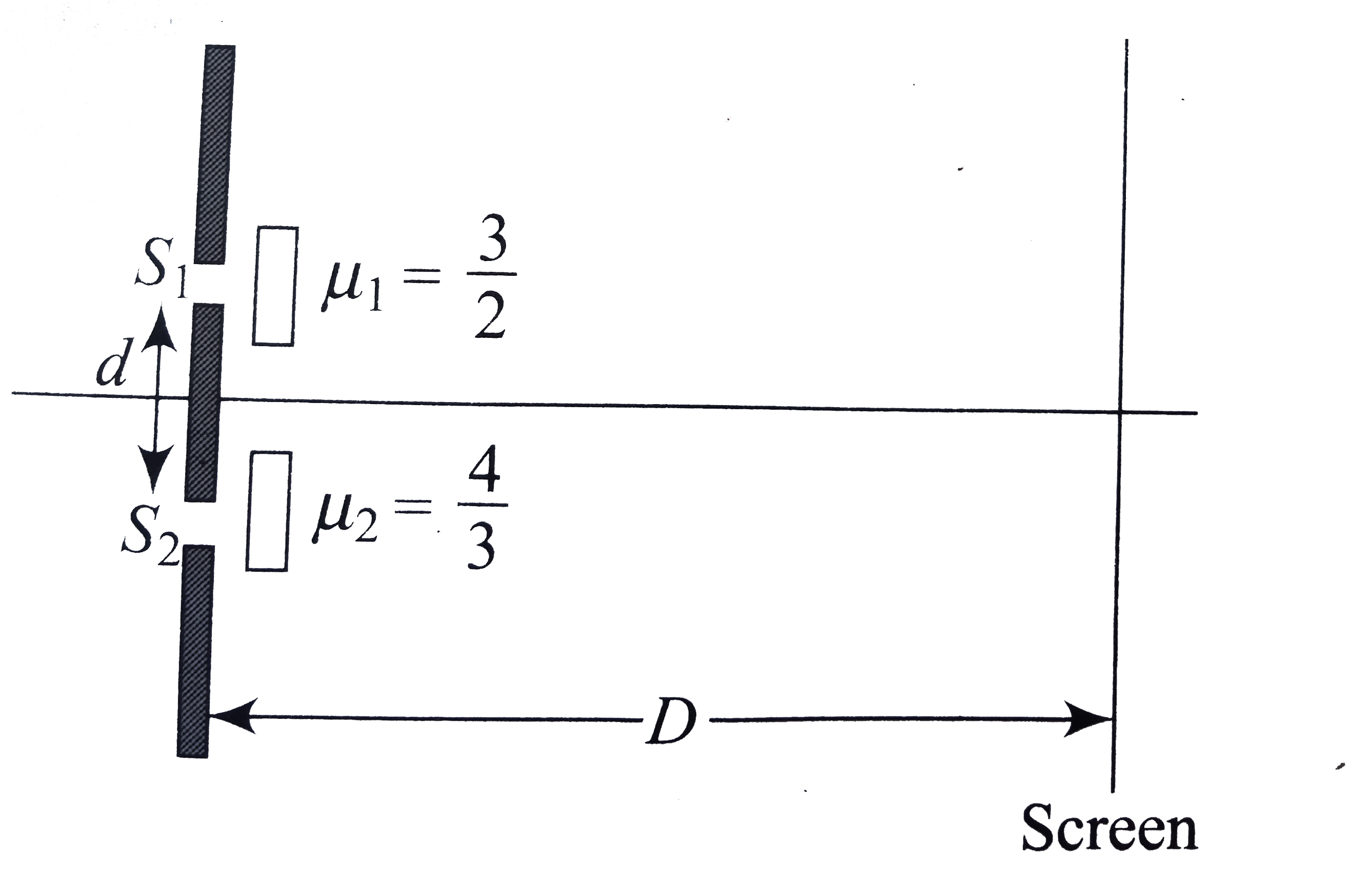
(c )Now,if 600nmlight is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O.[All wavelengths in this problem are for the given medium of refractive index 4/3 .Ignore dispersion]View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
 View Solution
View SolutionMinimum thickness of a mica sheet having μ=32 which should be placed in front of one of the slits in YDSE is required to reduce the intensity at the centre of screen to half of maximum intensity is
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen.
Find the value of n.View Solution

