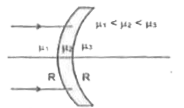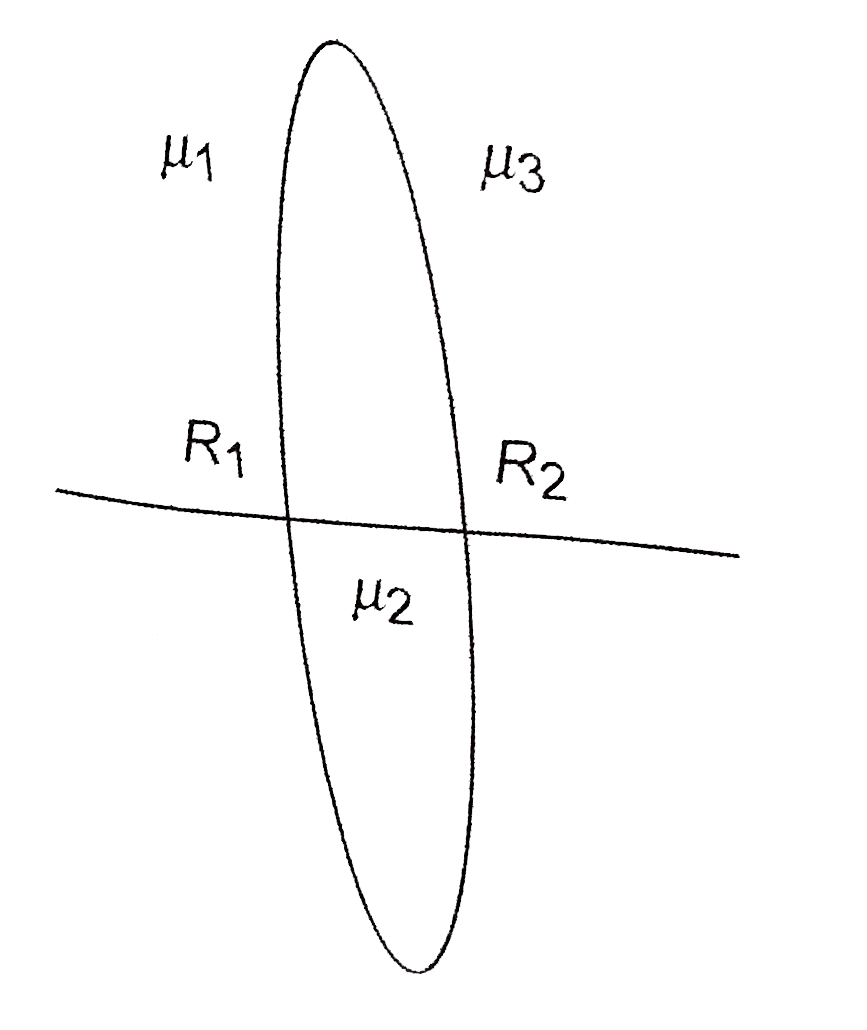
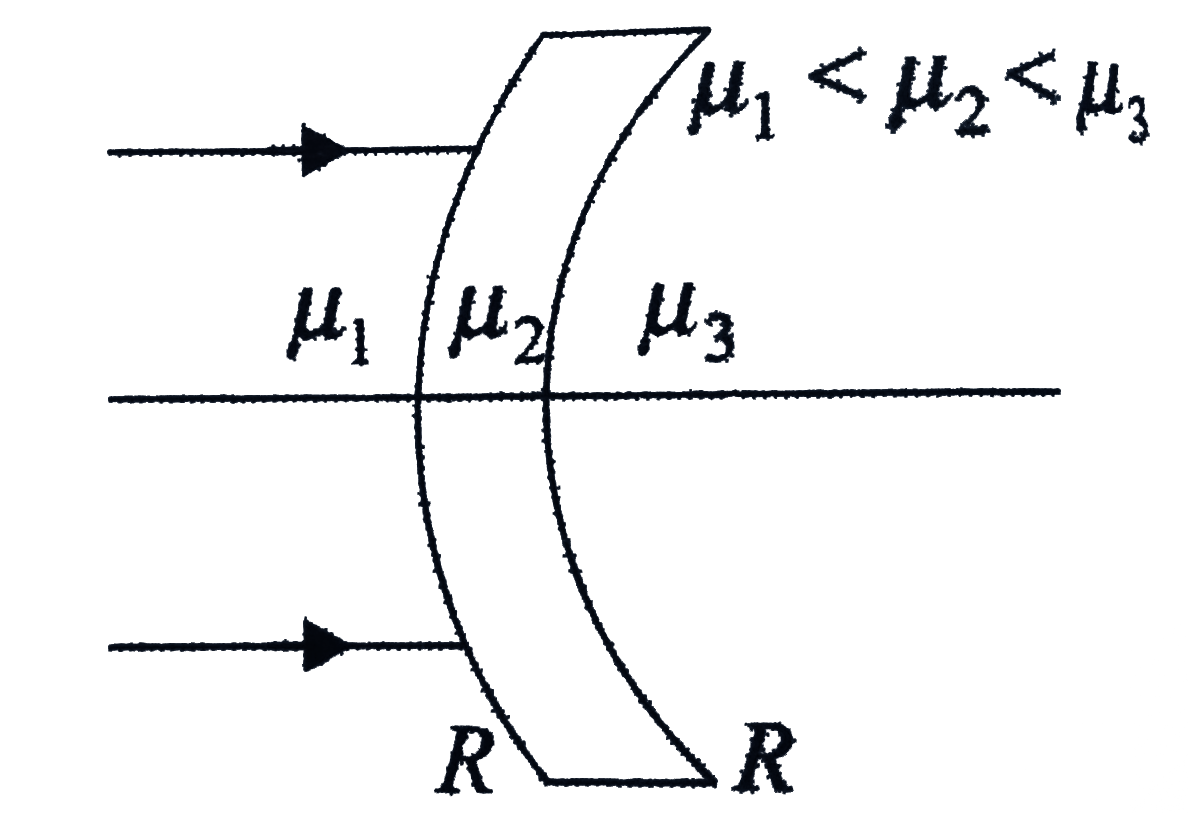
Find the focal length of the lens as shown in figure.
If rays are incident from left:
Refraction at (1):
μ2v−μ1u=μ2−μ1R1 …(i)
Refraction at (2):
μ2v−μ1v=μ3−μ2R2 ….(ii)
Adding (i) and (ii)
(μ3v'−μ1u=μ2−μ1R1+μ3−μ2R2
if u=∞,v'=f2
μ3f2=μ2−μ1R1+μ3−μ2R2
If rays are incident from right, replace μ1 by μ3 and R1 by R2
μ1f1=μ2−μ3R2+μ1−μ2R1
If μ1μ3=1,f1=f2=f
1f=(μ−1)(1R1−1R2)
Topper's Solved these Questions
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- REFLECTION OF LIGHTBOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES
67 Videos
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
Similar Questions
Knowledge Check
A convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
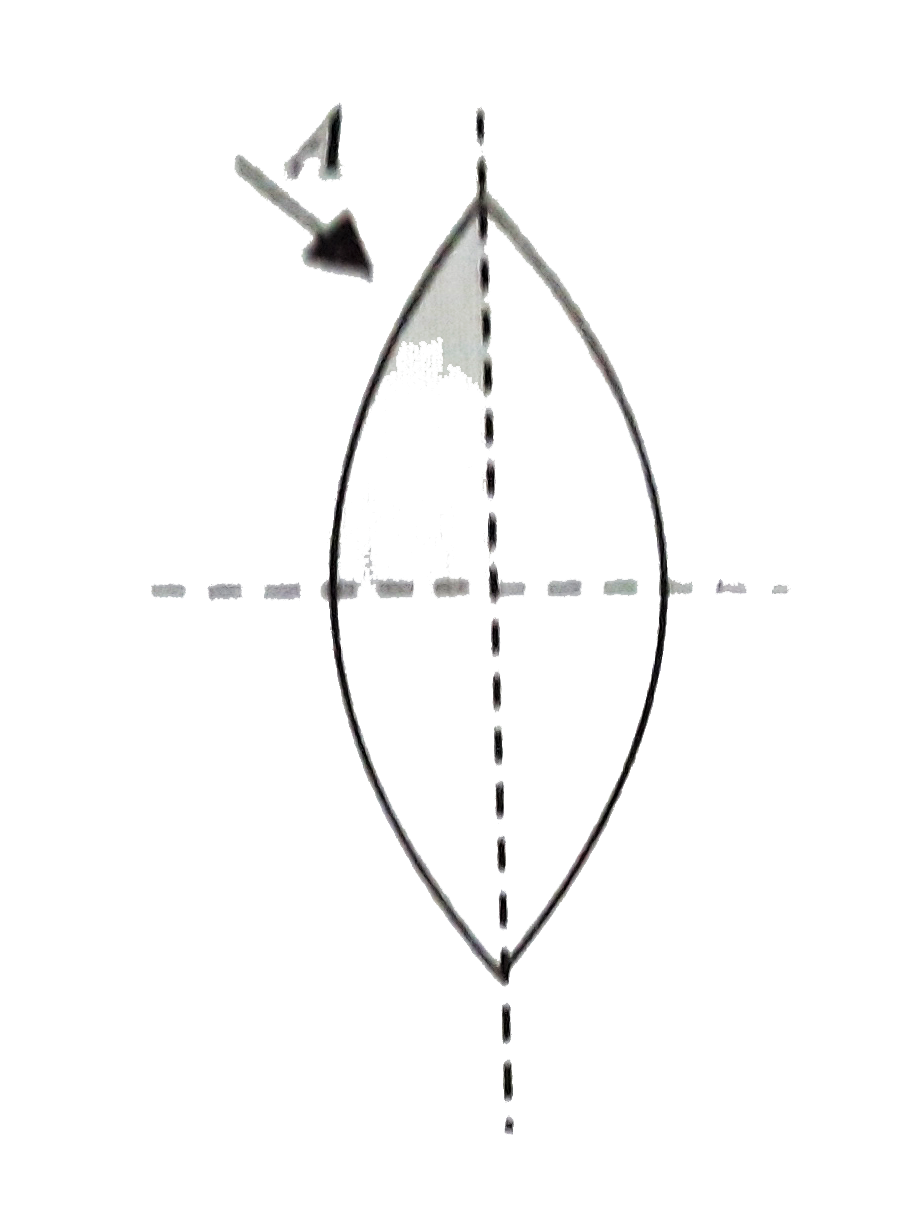 Af/2BfC4fD2f
Af/2BfC4fD2f
Find the focal length of the lens shown in Fig.
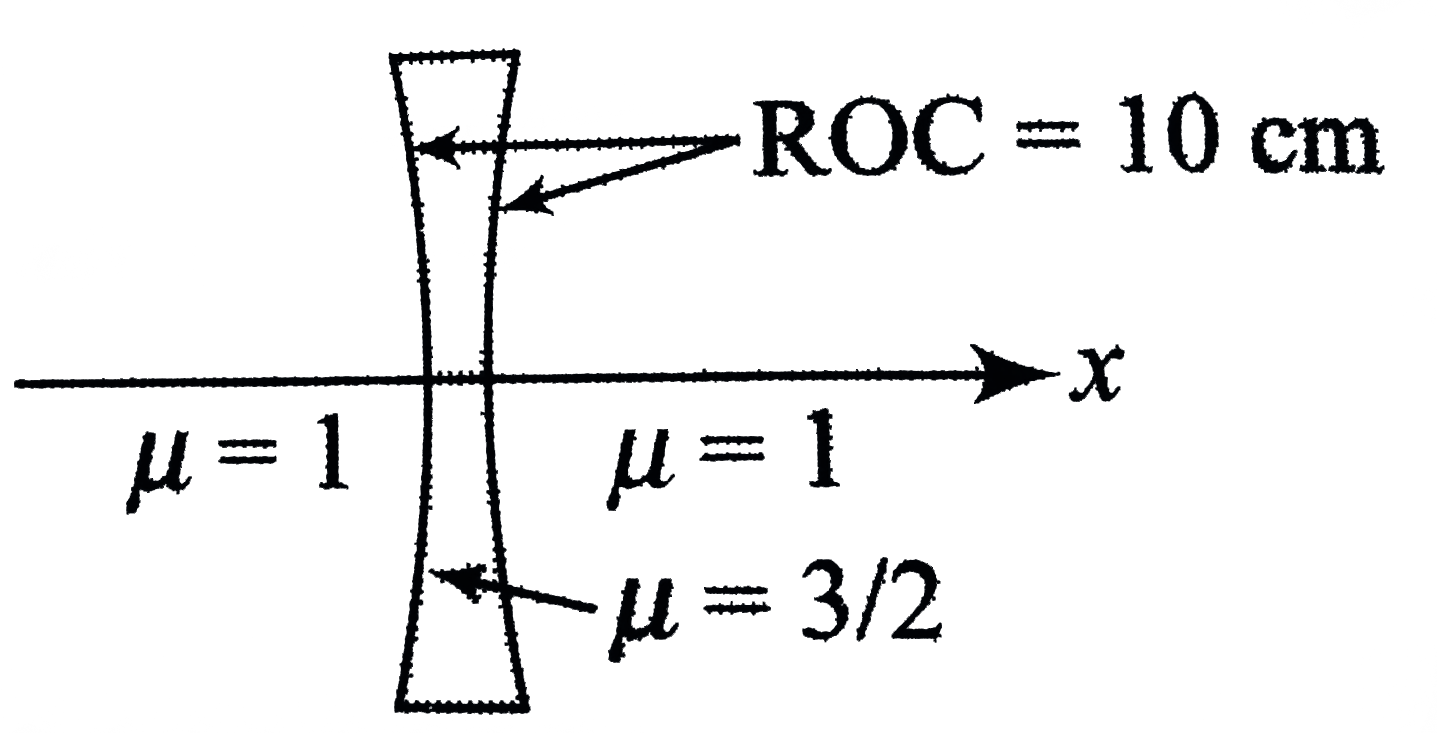
View SolutionFind the focal length of the lens shown in the Fig..
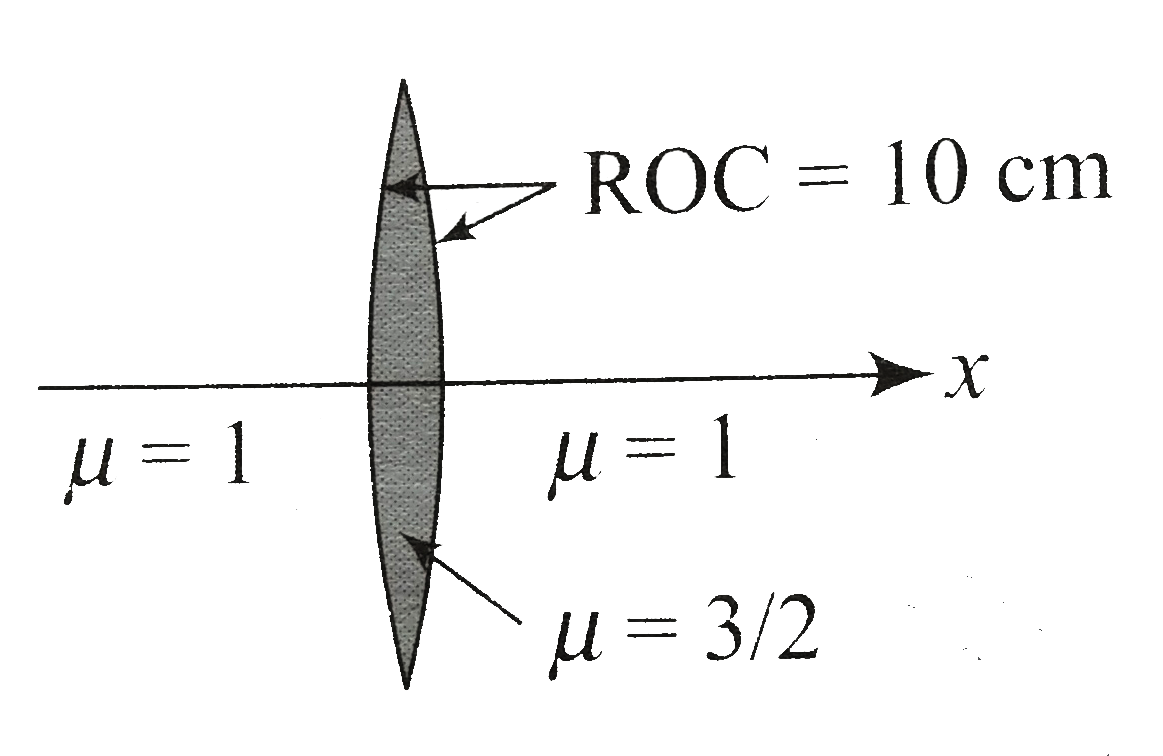
View SolutionFind the focal length of lens shown in the figure. Solve for three cases nS=1.5,nS=2.0,nS=2.5.
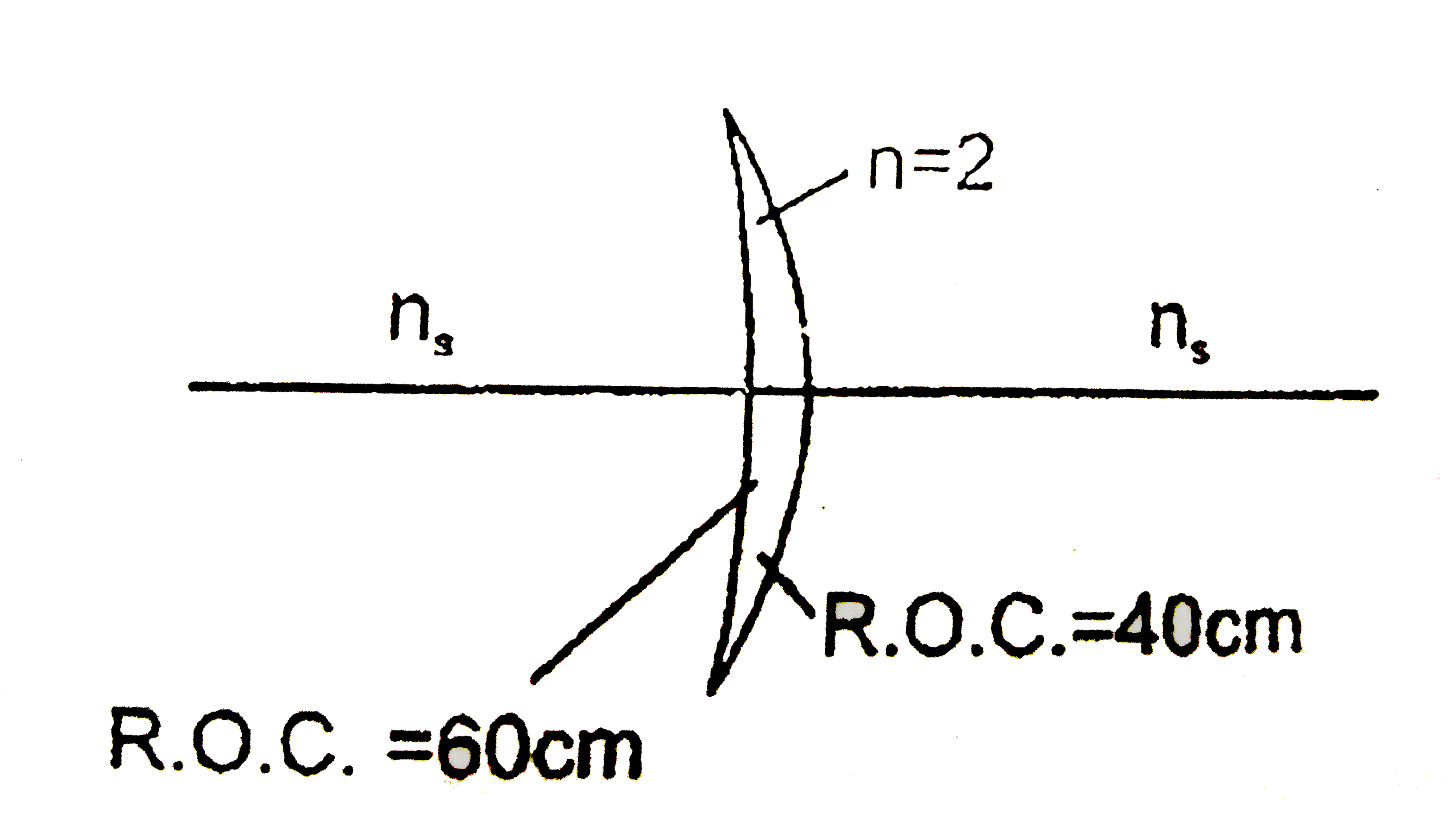
View SolutionCalculate the focal length of the lens shown in the figure.
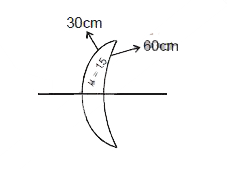
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View Solution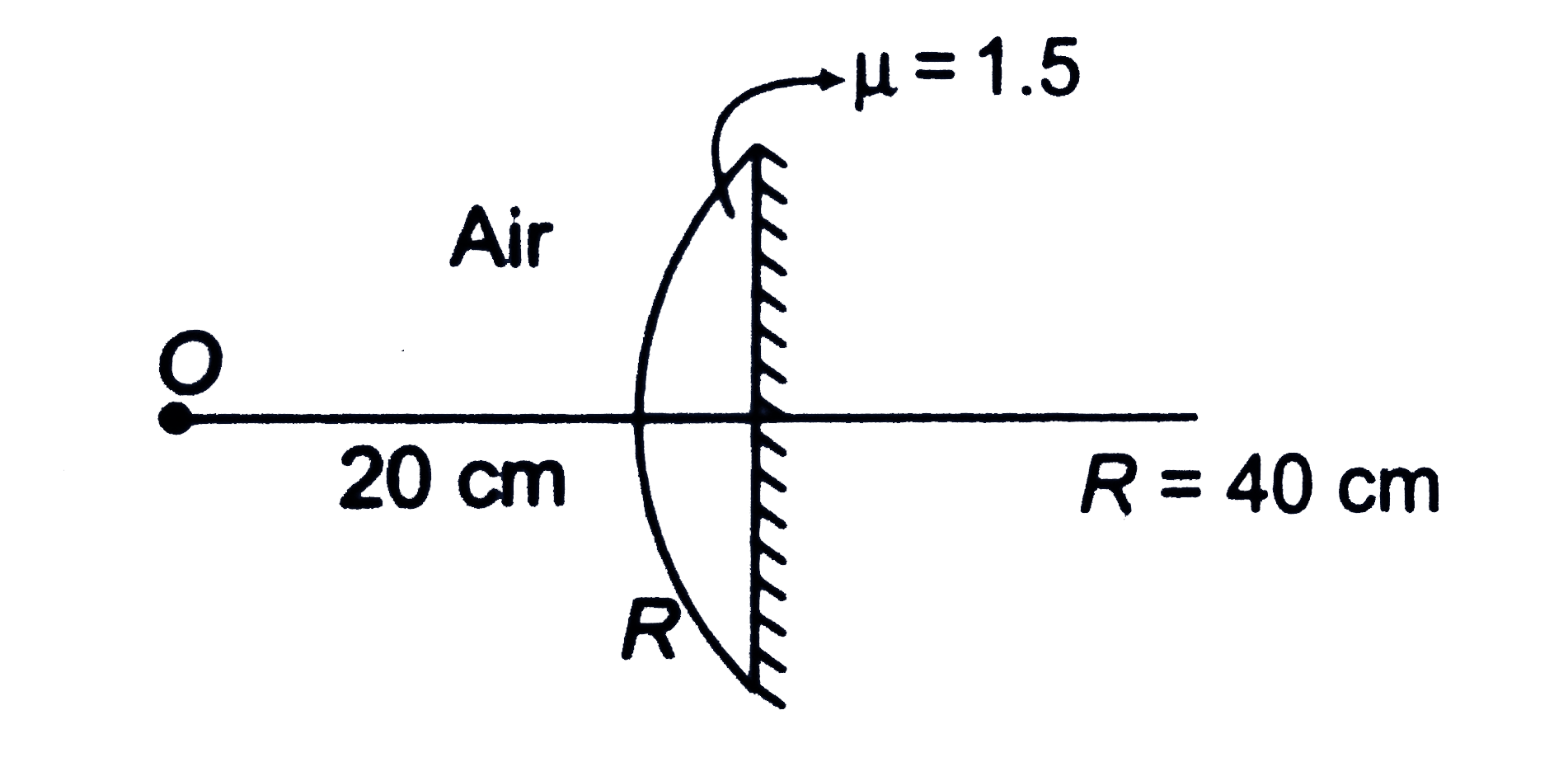
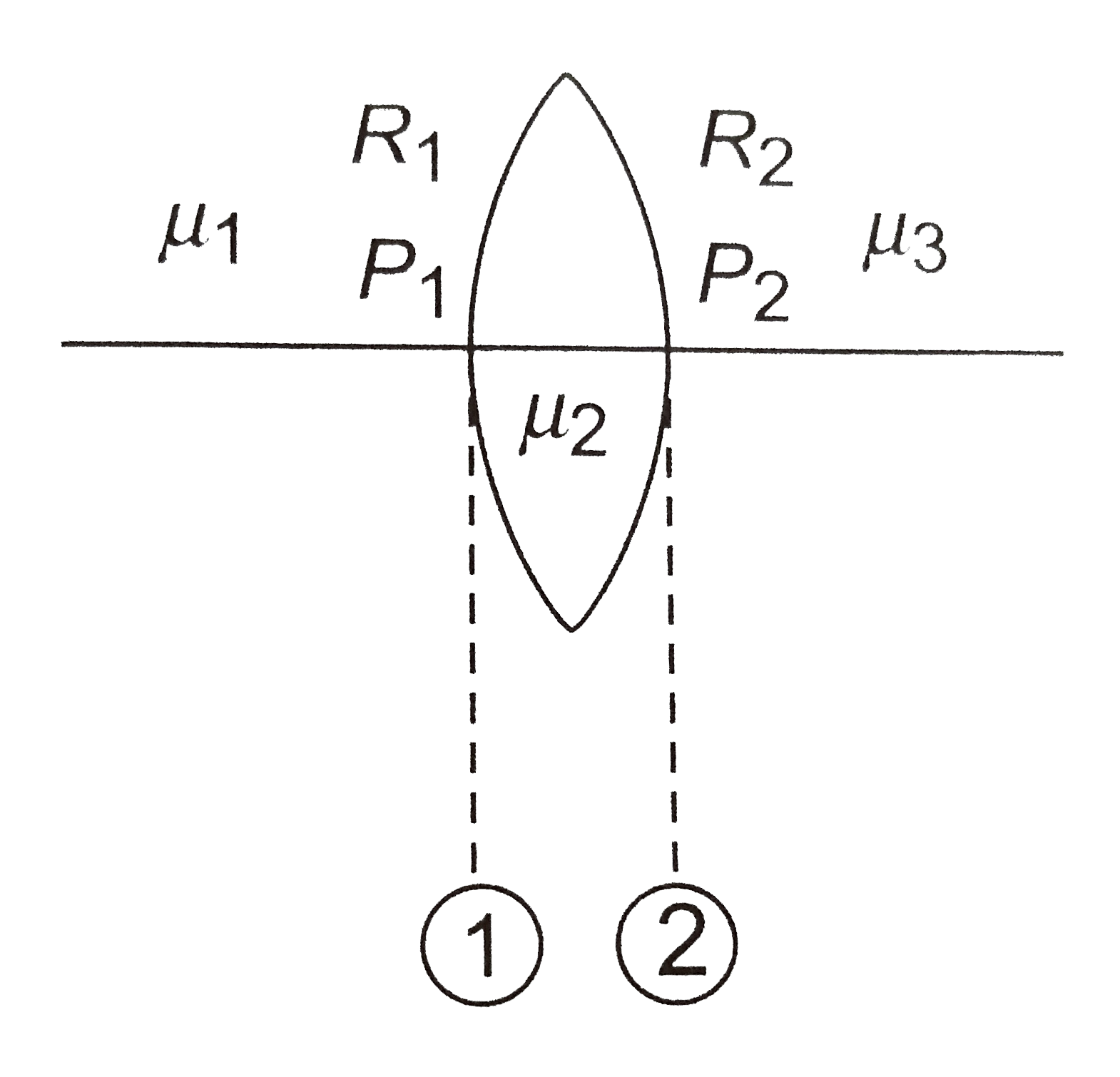
Find focal length of the system as shown if figure.
Find image position.
View SolutionA convex lens of glass (μ=1.5) is formed by combining two surfaces of radii R1=60cm and R2=30cm . It is cut into two parts in two different ways as shown in Figure .
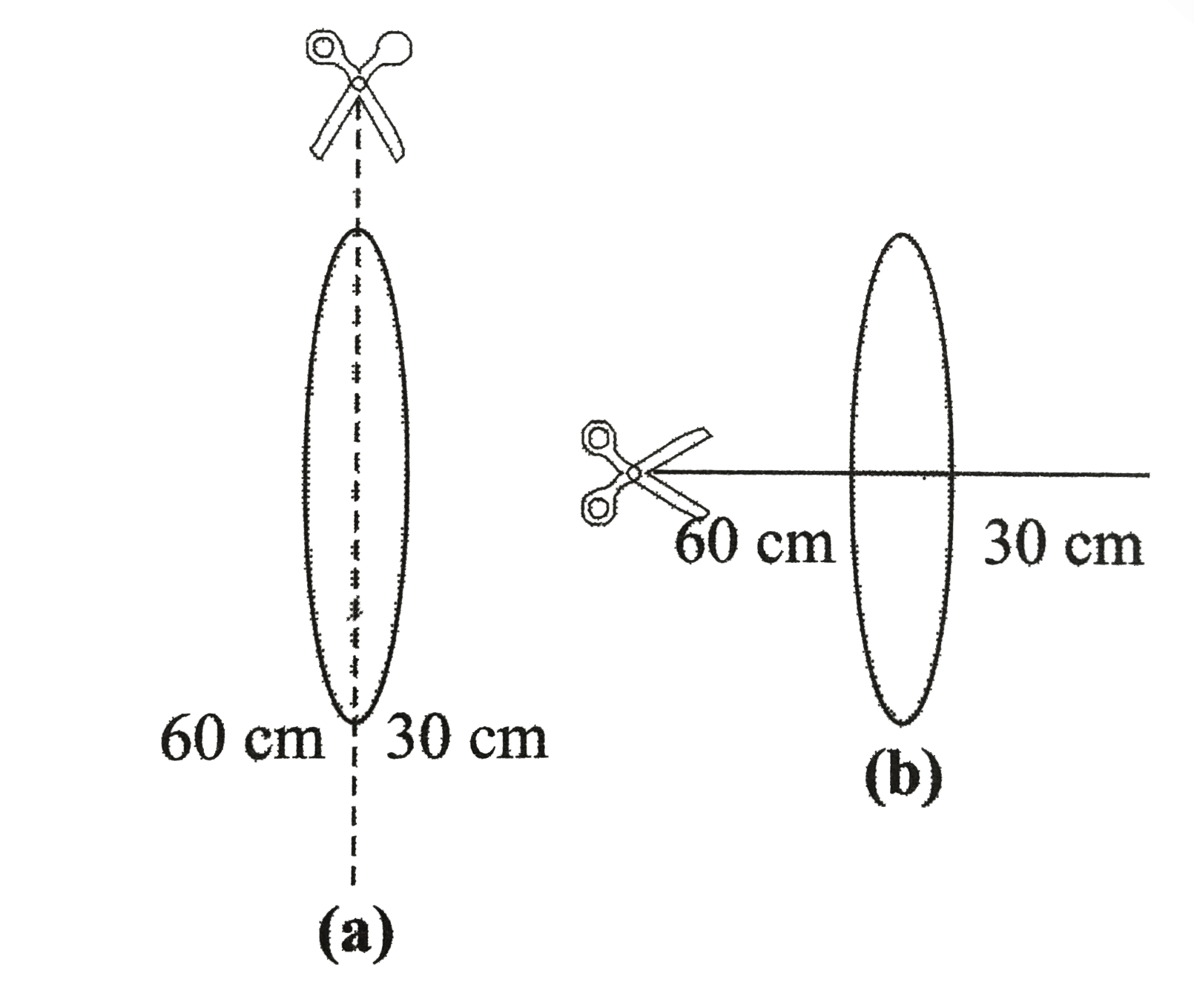
Find:
a. the focal length of the lens.
b. in figure (a), the focal length of left portion and that of the right portion.
c. in figure (b), the focal length of the upper part and that of the lower part.
View Solution