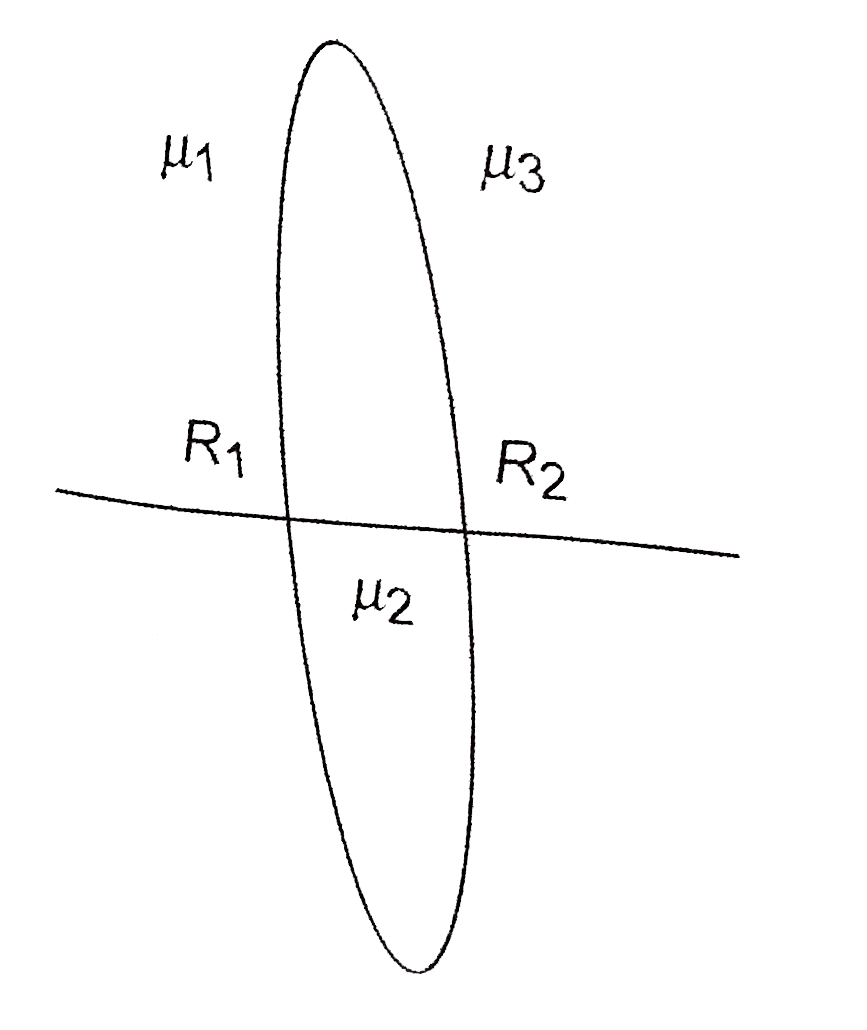
A convex lens of glass (μ=1.5) is formed by combining two surfaces of radii R1=60cm and R2=30cm . It is cut into two parts in two different ways as shown in Figure .
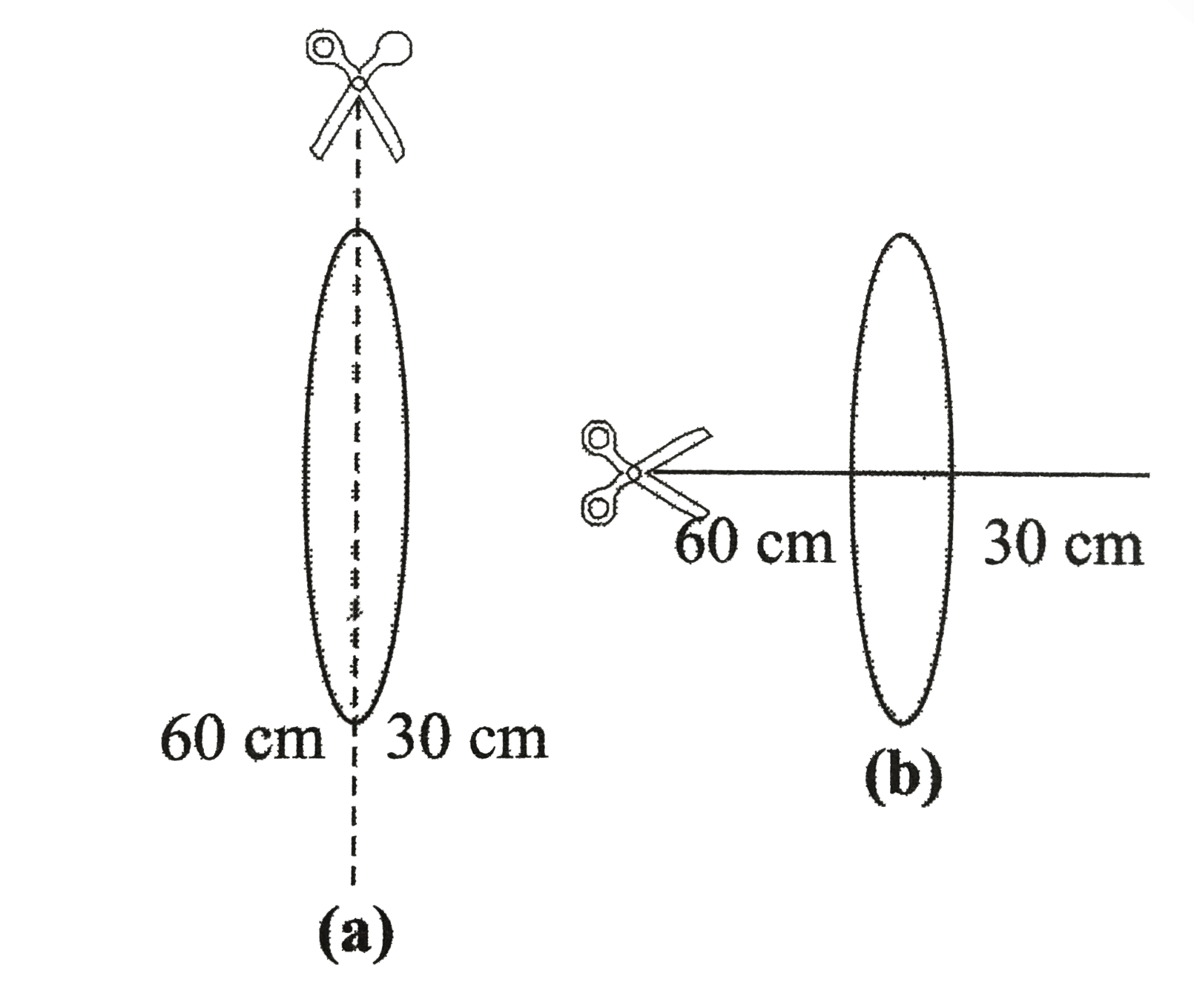
Find:
a. the focal length of the lens.
b. in figure (a), the focal length of left portion and that of the right portion.
c. in figure (b), the focal length of the upper part and that of the lower part.
a. Using Lensmaker's formuls, we get
1f=(1.5−1)(130−1−60)=12(130+160)=140
⇒f=+40cm
b. The focal length of the left position is given by
1f1=(1.5−1)(160−1∞)=1120
⇒f1=+20cm
and, the focal length of the right portion is give by
1f1=(1.5−1)(1∞−1−30)=160
⇒f2=60cm
c. Since the refracting surfaces remaing unchanged, therefore the focal lengths of the upper part and the lower part are equal, i.e.,
f1=f2=+40cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Single Correct
221 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
Knowledge Check
If the bio-convex lens is cut as shown in the figure, the new focal length f' isA2fBfC(f)/(2)DInfiniteA convex lens has a focal length f. It is cut into two parts along the dotted line as shown in figure. The focal length of each part will be
 Af2BfC32fD2f
Af2BfC32fD2fThe focal length of the combination of two thin lenses in contact is 80 cm. If the focal length of one lens is -20 cm, what is the power of the other lens ?
A2.25 DB6.25 DC−2.5 DD−3.75 D
Find the focal length of the lens shown in the figure. The radii of curvature of both the surfaces are equal to R
View SolutionFocal length of the convex lens shown in figure is 20cm. Find the image position and image velocity.
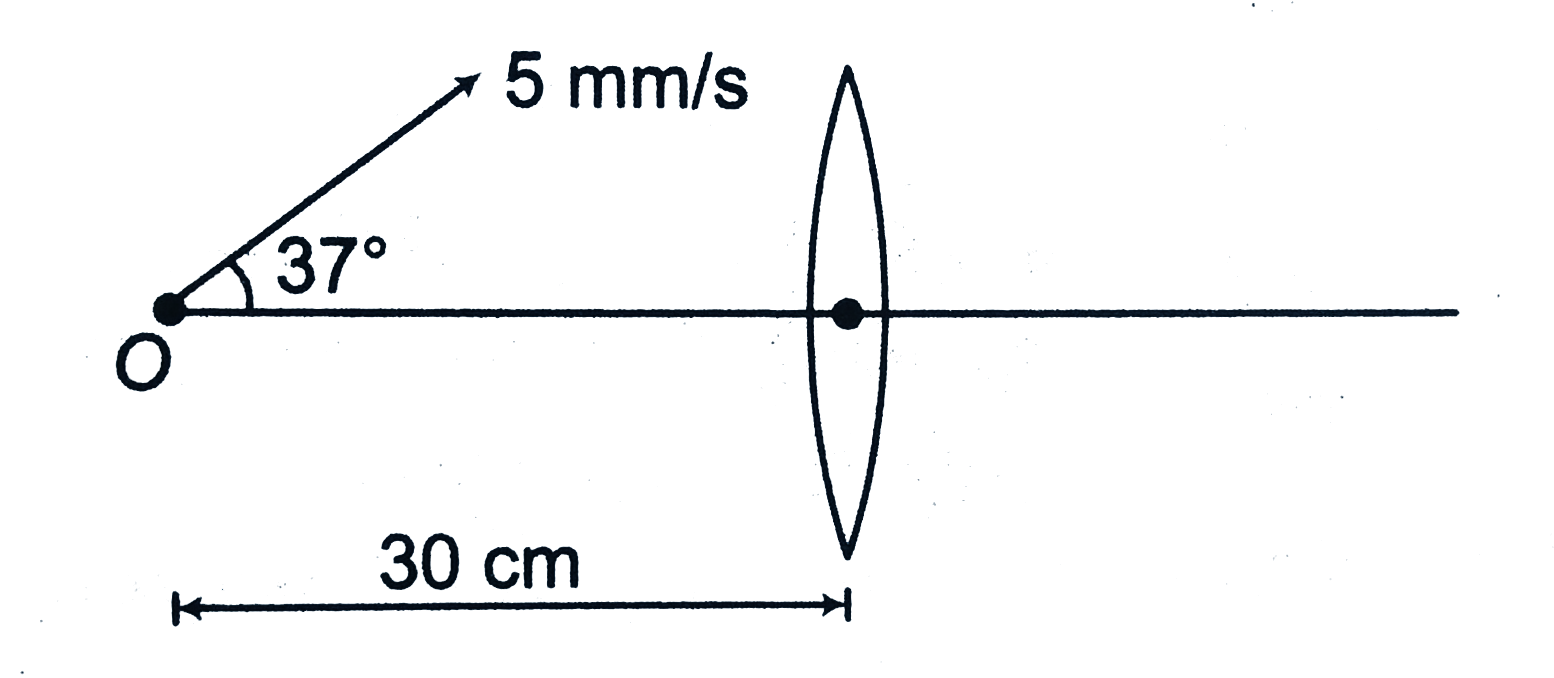
View SolutionThere are two spherical surfaces of radii R1=30cm and R2=60cm. In how many ways these surfaces may be arranged to get different lenses. If all the lenses are made of glass (μ=1.5) , find the focal length of each lens.

View SolutionA convex lens has a focal length f. It is cut into two parts along the dotted line as shown in figure. The focal length of each part will be

View SolutionA convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
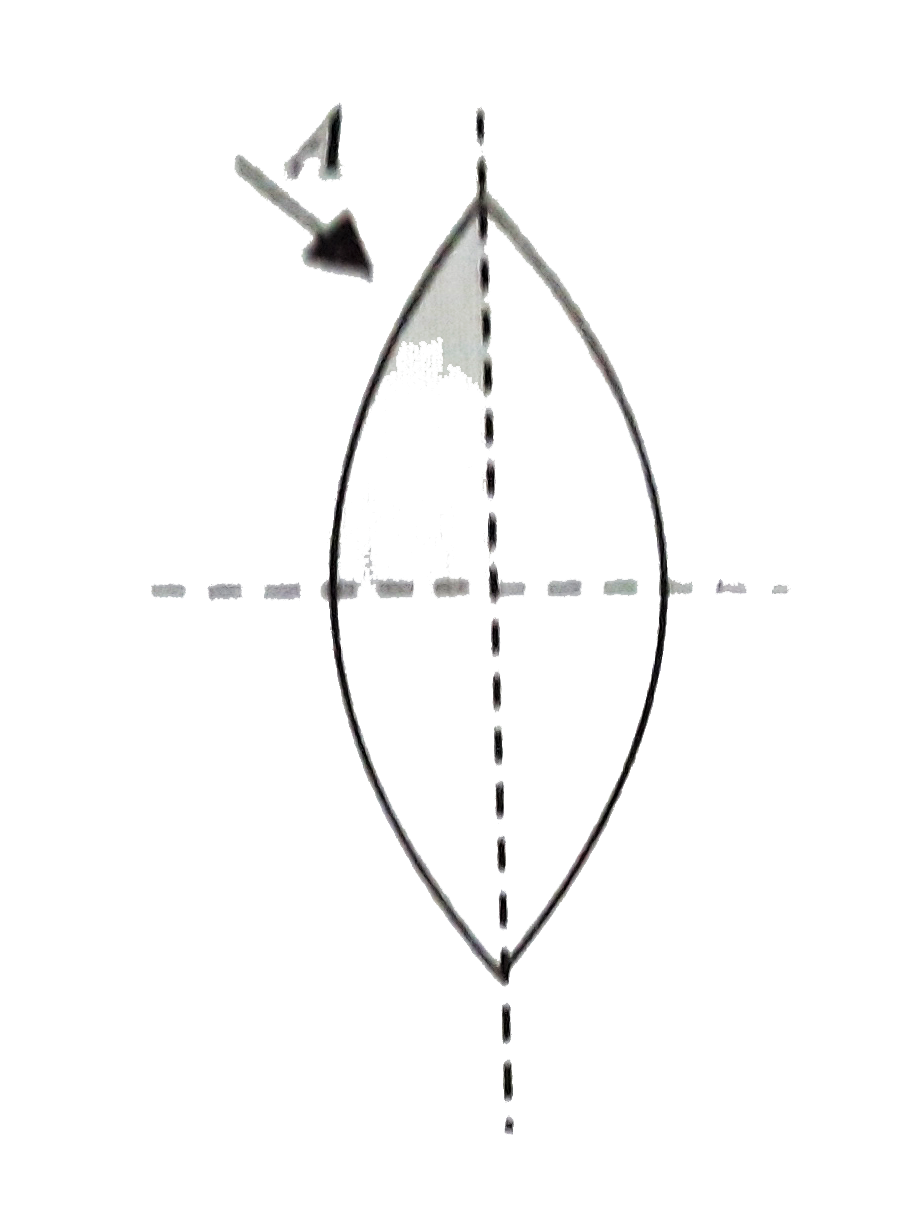
View Solution