A concave lens of glass, refractive index 1.5 has both surfaces of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will behave as a
convergent lens of focal length 3.5 R
convergent lens of focal length 3.0 R
divergent lens of focal length 3.5 R
divergent lens of focal length 3.0 R
The correct Answer is:A
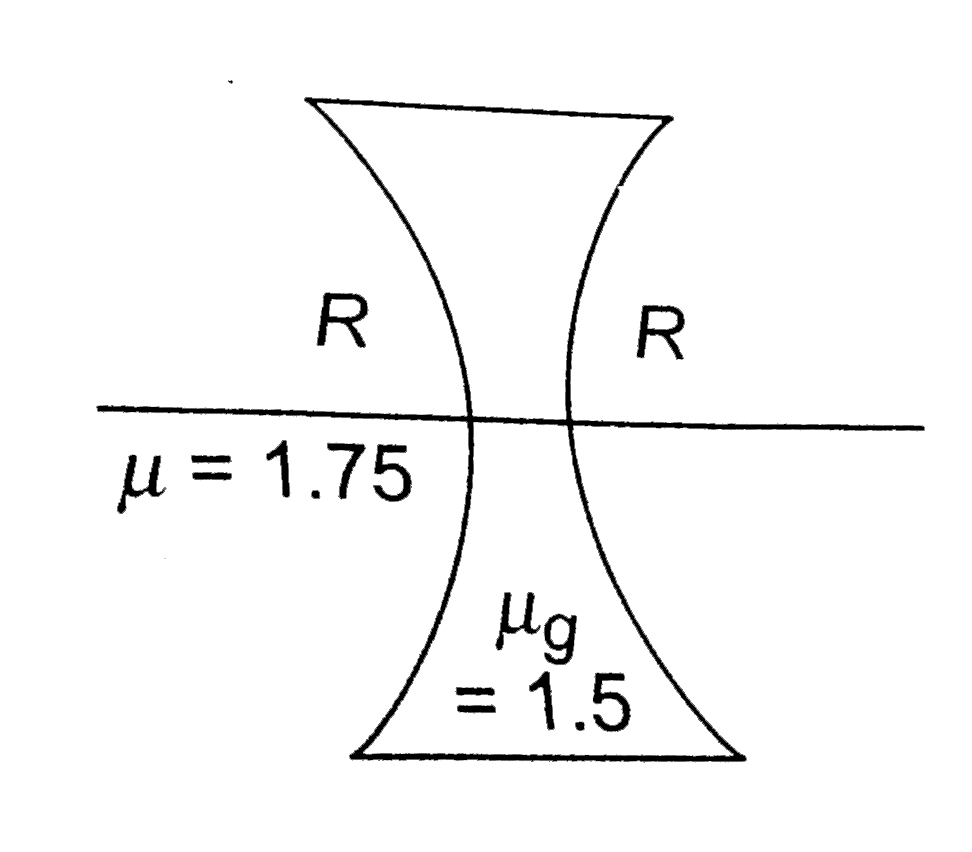
1f=(.aμg−1.aμl−1)(1R1−1R2)
=⎛⎝321.75−1⎞⎠(1−R−1R)
=(−17)(−2R)⇒f=3.5R
Since focal length is positive i.e., convergent lens
Topper's Solved these Questions
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- REFLECTION OF LIGHTBOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES
67 Videos
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
Similar Questions
A convax lens of glass ,refractive index1.5,has both surfaces of same radius of curvature R.On immersion in a medium of refractive index1.75,it wuill behaves as a
(A)convergent lens of focal length 3.5R(B)convergent lens of focal length 3.0R(C)divergent lens of focal length 3.5R(D)divergent lens of focal length 3.0R
View SolutionA convex lens made up of glass of refractive index 1.5 is dippedin turn
(i) in a medium of refractive index 1.65
(ii) in a medium of refractive index 1.33
(a) Will it behave as converging or diverging lens in the two cases ?
(b) How will its focal length changes in the two media ?
View Solution
Knowledge Check
A concave lens of glass, refractive index 1.5, has both surface of same radius of curvature R. On immersion in a medium of refractive index 1.75, it will have as a
Aconvergent lens of focal length 3.5R.Bconvergent lens of focal length 3.0R.Cdivergent lens of focal length 3.5R.Ddivergent lens of focal length 3.0R.A thin glass (refractive index 1.5) lens has optical power of −5D in air. Its optical power in a liquid medium with refractive index 1.6 will be
A−1DB1DC−25DD25DThe focal length of a convex lens of glass of refractive index 1.5 is 2 cm. The focal length of the lens when immersed in a liquid of refractive index 1.25 will be:
A2.5 cmB5 cmC1 cmD4 cm
A convex lens made up of glass of refractive index 1.5 is dipped, in turn, in (i) a medium of refractive index 1.65, (ii) a medium of refractive index 1.33.
(a) Will it behave as a converging or a diverging lens in the two cases ?
(b) How will its focal length change in the two media ?
View SolutionA double convex lens of +5D is made of glass of refractive index 1.5 with both faces of equal radii of curvature. Find the value of curvature.
View SolutionA diverging lens of refractive index 1.5 and focal length 15cm in air has same radii of curvature for both sides. If it is immersed in a liquid of refractive index 1.7, calculate focal length of the lens in liquid.
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionA thin convex lens made of glass of refractive index 3/2 has a power of 5 D. When it is immersed in a liquid of refractive index μ, it behaves like a divergent lens of focal length 1 m. Calculate the refractive index of the liquid.
View Solution
