Find the focal length of lens shown in the figure. Solve for three cases .
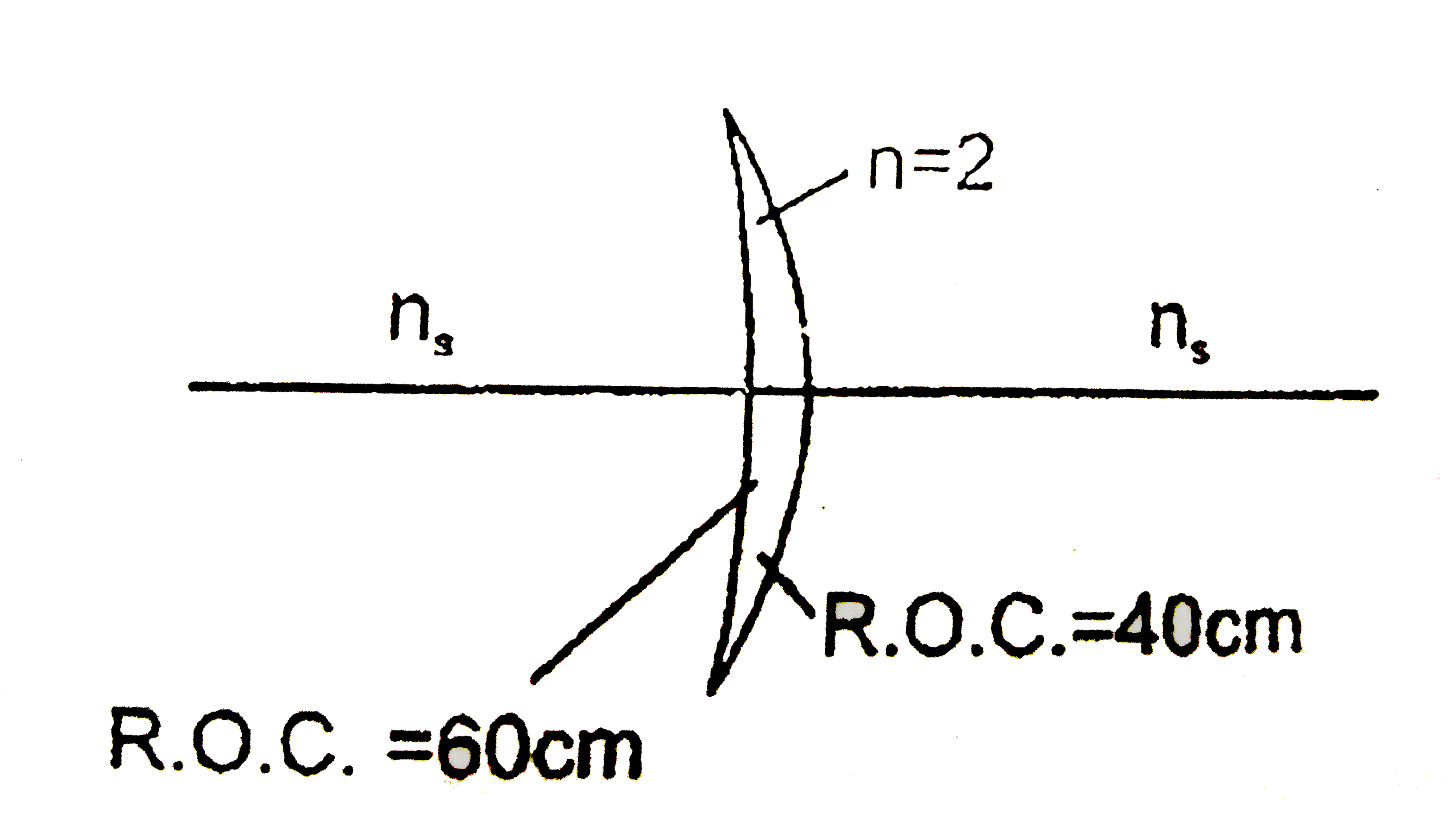
The correct Answer is:
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
63 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
79 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
Knowledge Check
In n(A)=2,P(A)=15, then n(S)=?
A10B2C5D20Consider two palne convex lanse of same radius of curvature and refrective index n1 and n2 respectively. Now consider two cases :
_PHY_E01_001_Q01.png)
Case - I : When n1=n2=n, then equivalent focal length of length is f0
Case - II : When n1=n,n2=n+Δn, then equilivant focal length of lens is f=f0+Δf0
Then correct options are :AIf Δn/n>0, then Δf0/f0<0B|Δf0/f0|<|Δn/n|CIf n=1.5,Δn=10−3 and f0=20 cm then |Δf0|=0.02 cmDIf Δn/n<0, then Δf0/f0>0In the formulae Sn=n2{2a+(n−1)d} make d as the subject
The following steps are involved in solving the above problem. Arrange them in sequential order.
(A) (n−1)d=2Snn−2a
(B) Given, Sn=n2[2a+(n−1)d]⇒n[2a+(n−1)d]
=2Sn
(C) ⇒d=2n−1[Snn−a]
(D) 2a+(n−1)d=2SnnADBACBBDACCABDCDBDCA
Two coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
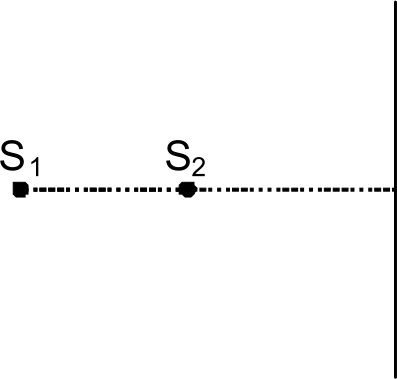
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionLet S1,S2…., be squares such that for each n≥1 , the length of a side of Sn equals the length of a side of Sn equals the length of a diagonal of Sn+1. If the length of a side S1 is 10 cm, then for which of the following value of n is the area of Sn less than 1 sq cm ?
View SolutionLet S1,S2 , …. Be squares such that for each n≥1 the length of a side of Sn equals the lengths of a diagonal of Sn+1 . If the length of a sides of S1 is 10 cm, then for which of the following values of n is the area of Sn less than 1 square cm ?
View SolutionIf n(A)=2,P(A)=15,then n(S)=?
View SolutionA clock is started at 12 o'clock noon. By 10 minutes past 5, the hour hand has turned through
View Solution
