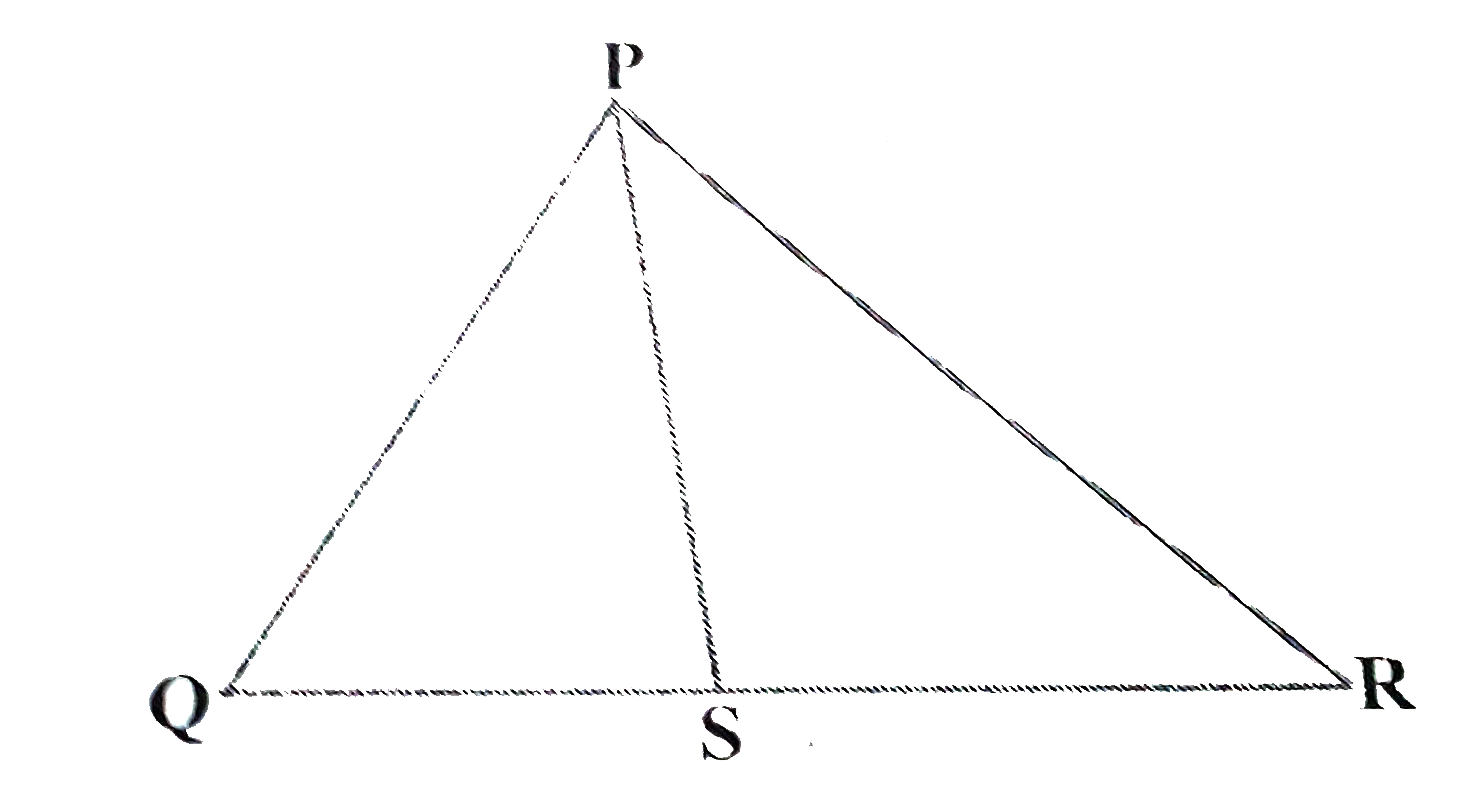
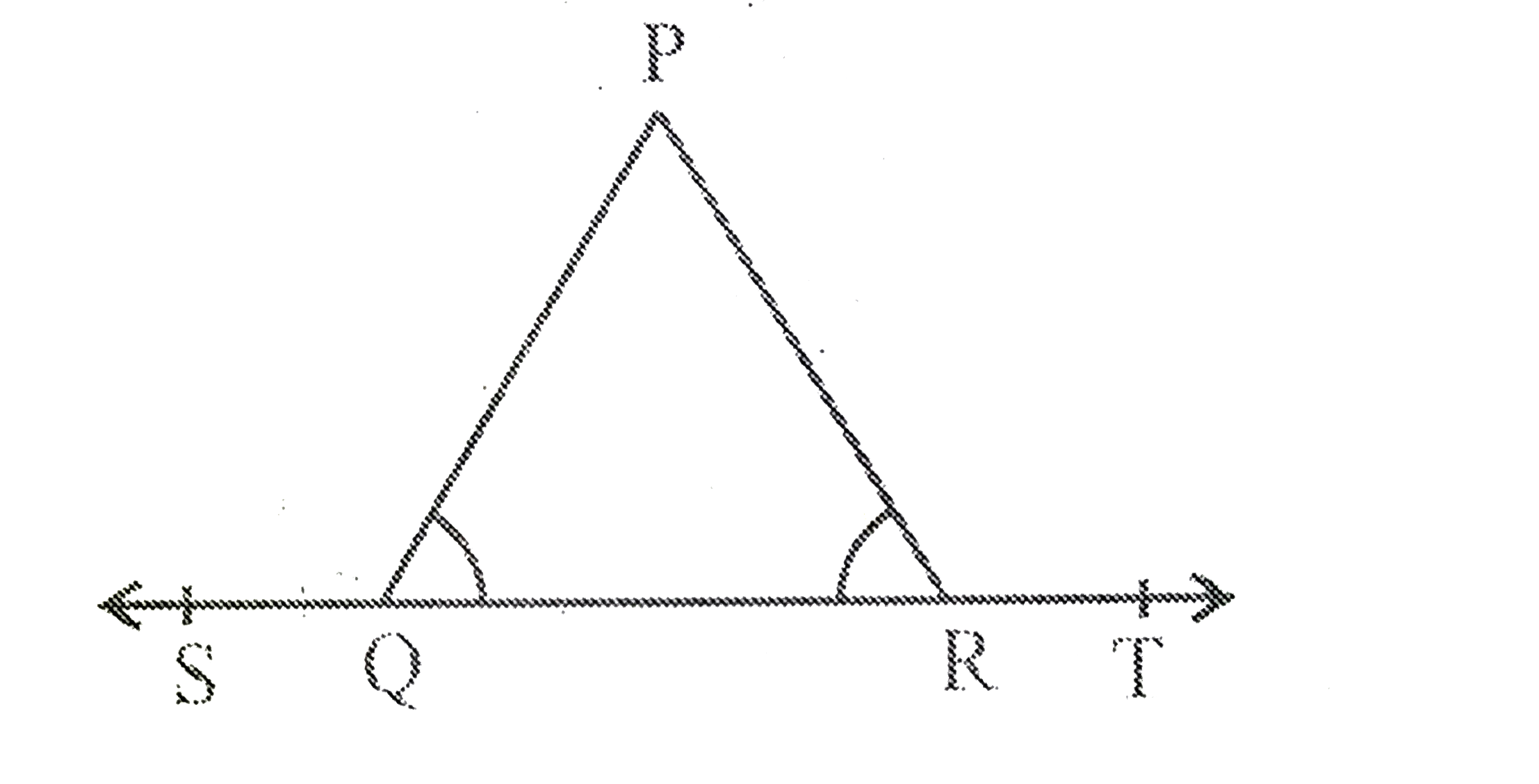
In Figure PS is the bisector of ∠QPR and PT ⊥QR . Show that ∠TPS=12(∠Q−∠R)
Solution; We know that angle 'QPS = 12 angle P ..(1)'
angle Q + angle QPT=90∘
angle QPT=90∘ -angle Q ....(2)
On putting equations '(1)' and '(2)'
angle TPS = angle QPS - angle QPT
= 12angle P−(90−∠Q) = 12 angle P−90 + angle Q
= 12 angle P−12(angle Q +angle P + angle R) + angle Q
= 12 angle P−12 angle Q−12 angle P−12 angle R + angle Q
= −12 angle Q−12 angle R+ (+ve and -ve 12 angle P
by taking LCM in angle Q we get
−12 angle Q+22angle Q−12 angle R
angle Q got cancelled)
(−12+22) angle Q−12 angle R=12 angle Q−12 angle R
angle TPS = 12 (angle Q−12∠R)
Related Playlists
Similar Questions
In figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
 View Solution
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
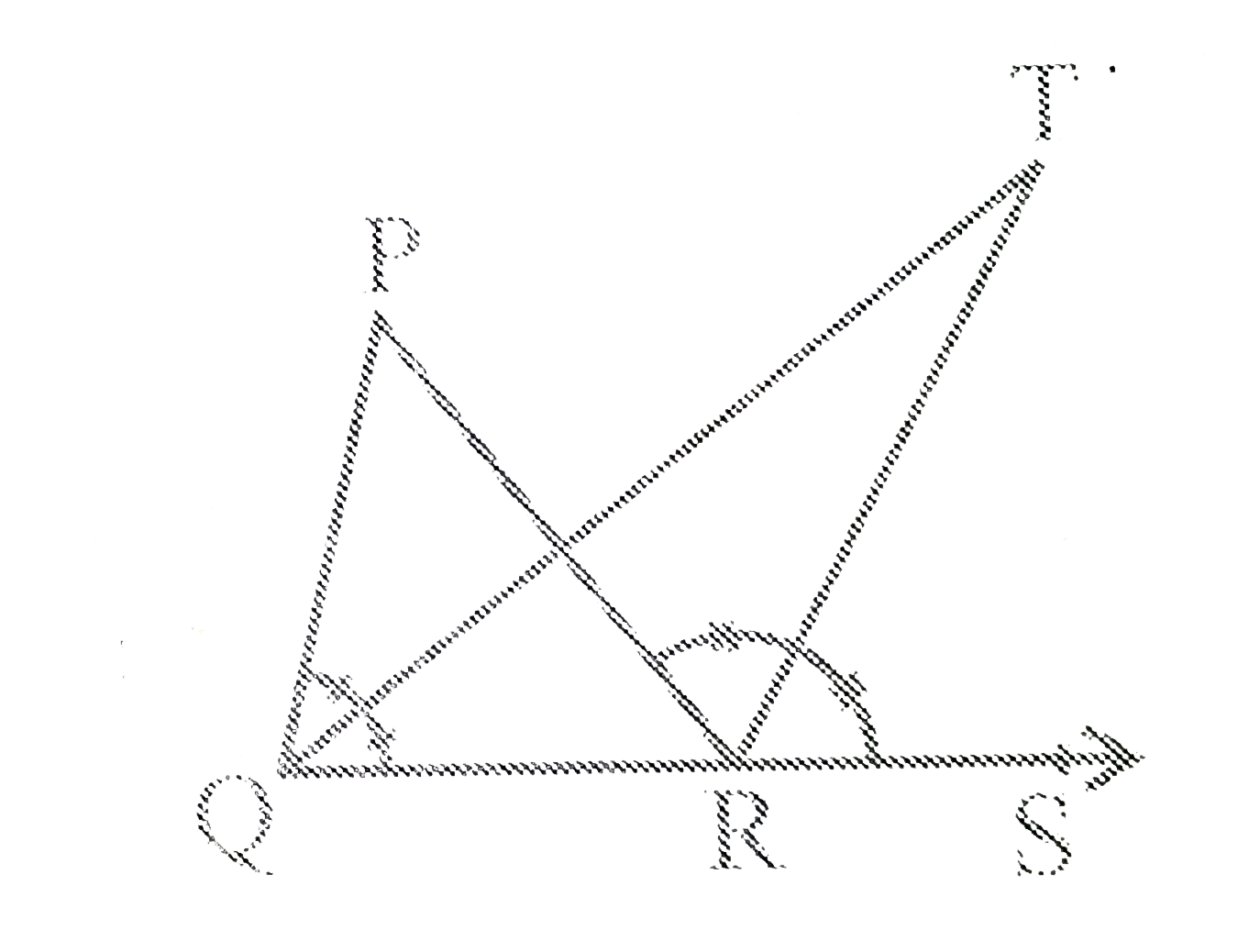 View Solution
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
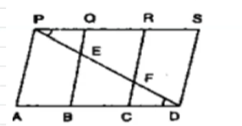 View Solution
View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
 View Solution
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
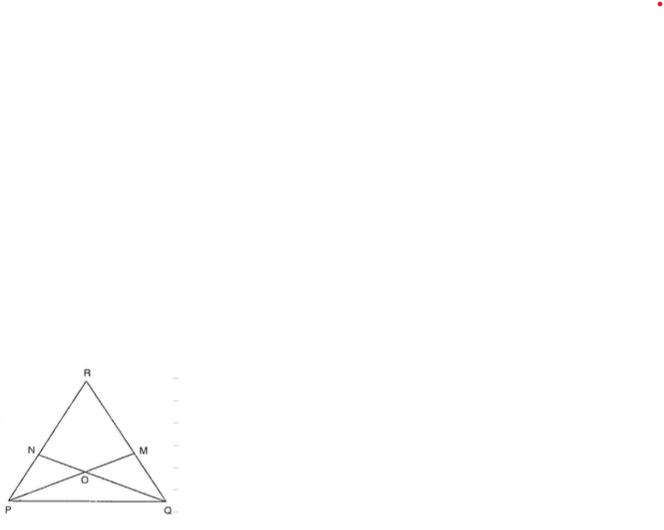 View Solution
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
 View Solution
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 View Solution
View Solution


