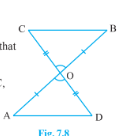
OA = OBand OD = OC. Show that (i)ΔAOD≅ΔBOC and (ii)AD ∣∣ BC
To solve the problem, we need to show that triangles ΔAOD and ΔBOC are congruent and that lines AD and BC are parallel. Let's break this down step by step.
Step 1: Given Information
We are given that:
- ∠OA=∠OB (let's denote this as x)
- ∠OD=∠OC (let's denote this as y)
Step 2: Identify Angles in Triangles
In triangles ΔAOD and ΔBOC:
- In triangle ΔAOD:
- ∠AOD=180∘−(x+y) (since the sum of angles in a triangle is 180∘)
- In triangle ΔBOC:
- ∠BOC=180∘−(x+y)
Step 3: Establish Congruence of Triangles
To show that ΔAOD≅ΔBOC:
- We have:
- ∠OA=∠OB (given)
- ∠OD=∠OC (given)
- ∠AOD=∠BOC (as shown above)
By the Angle-Angle-Angle (AAA) criterion for triangle congruence, we can conclude that:
ΔAOD≅ΔBOC
Step 4: Show that Lines AD and BC are Parallel
Since ΔAOD≅ΔBOC, corresponding angles are equal. Therefore:
- ∠OAD=∠OBC
According to the Alternate Interior Angles Theorem, if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the lines are parallel. Thus, we can conclude:
AD∥BC
Conclusion
We have shown that:
(i) ΔAOD≅ΔBOC
(ii) AD∥BC
---
We are given that:
- ∠OA=∠OB (let's denote this as x)
- ∠OD=∠OC (let's denote this as y)
In triangles ΔAOD and ΔBOC:
- In triangle ΔAOD:
- ∠AOD=180∘−(x+y) (since the sum of angles in a triangle is 180∘)
- In triangle ΔBOC:
- ∠BOC=180∘−(x+y)
To show that ΔAOD≅ΔBOC:
- We have:
- ∠OA=∠OB (given)
- ∠OD=∠OC (given)
- ∠AOD=∠BOC (as shown above)
ΔAOD≅ΔBOC
Since ΔAOD≅ΔBOC, corresponding angles are equal. Therefore:
- ∠OAD=∠OBC
AD∥BC
We have shown that:
(i) ΔAOD≅ΔBOC
(ii) AD∥BC
Topper's Solved these Questions
Similar Questions
In Fig. 7.8, OA = OBand OD = OC. Show that (i)ΔAOD≅ΔBOC and (ii)AD ∣∣ BC.
View SolutionABCD is a quadrilateral in which and∠DAB =∠CBA(see Fig. 7.17). Prove that
(i) ΔABD≅ΔBAC
(ii) BD = AC
(iii) ∠ABD =∠BAC

View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
View SolutionABCD is a trapezium in which ABCD . The diagonals AC and BD intersect at O . Prove that (i) AOBCOD (ii) If OA=6cm , OC=8cm , Find: Area (AOB)Area (COD) (b) Area (AOD)Area (COD)
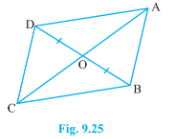
View SolutionIn Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:(i) ar (DOC) = ar (AOB)(ii) ar (DCB) = ar (ACB)(iii) D A\ ||\ C
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2

View SolutionA point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. Given: A rectangle ABCDandO is a point inside it. OA,OB,OCandOD have been joined. To Prove: ar(AOD)+ar(BOC)=ar(AOB)+ar(COD)
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View Solution
