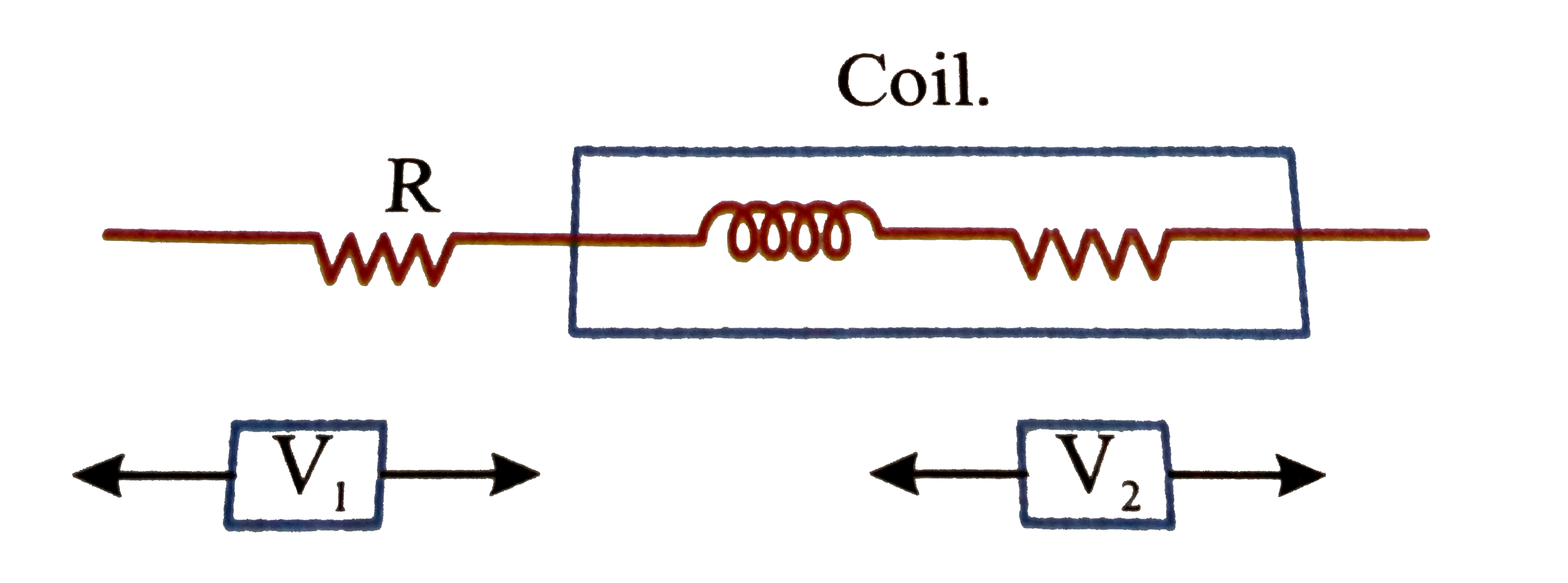
A resistor R is connected in series with a coil. The system is subjected to an AC supply of peak voltage V0. If the peak voltages dropped across the resistor R and the coil are V1 and V2 respectively
(a) The powerr dissipated in the coil is
V20−V21−V222R
The power dissipated in the circuit is
V20+V21−V222R
Only (a) is correct
Only (b) is correct
(a),(b) are wrong
(a),(b) are correct
The correct Answer is:D
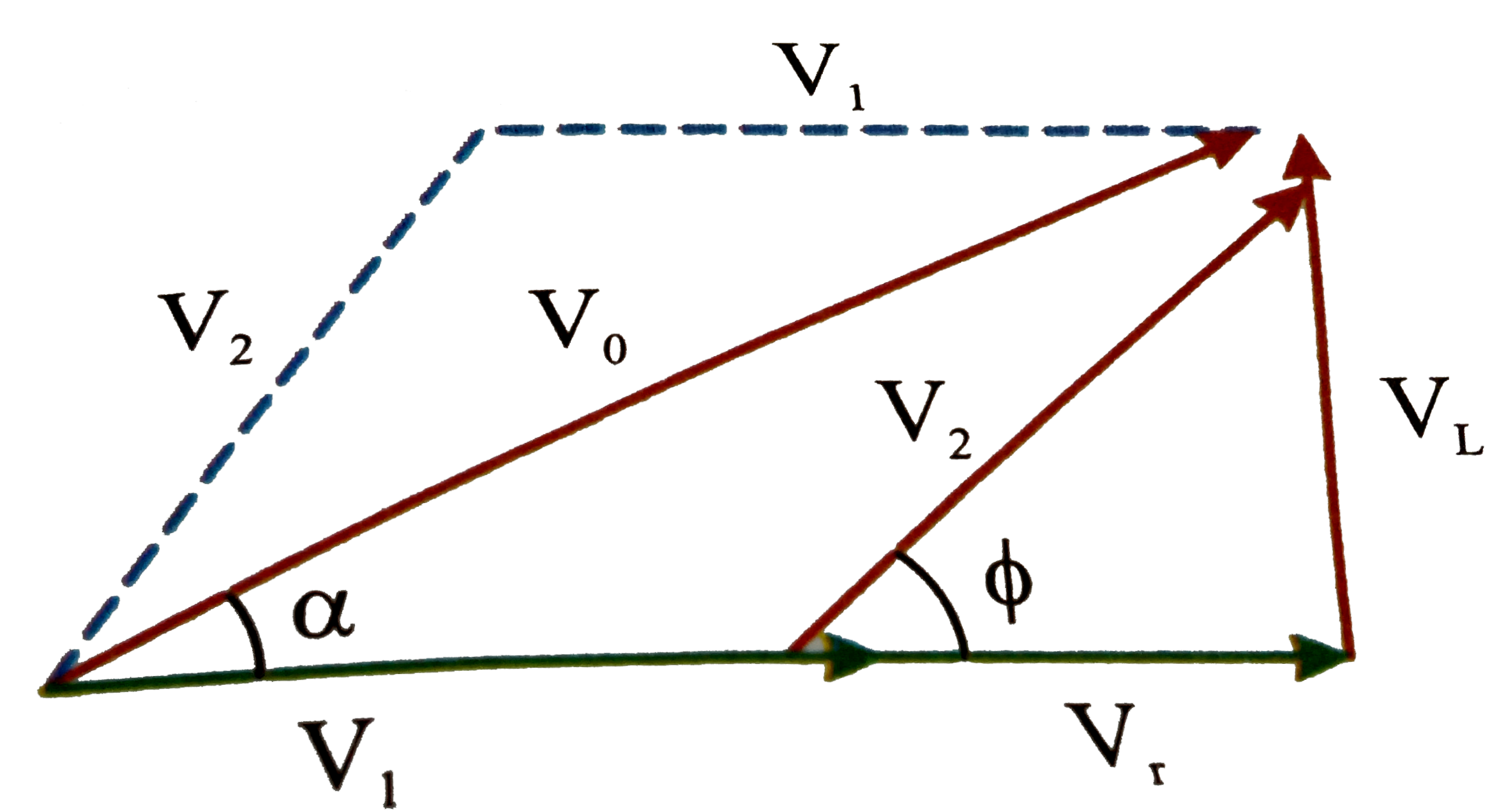
Power dissipated in the coil is
P=iV2cosϕ ….(1)
and V20=V21+V22+2V1V2cosϕ …..(2)
and i=V1R ….(3)
Solving P=V20−V21−V222R
Total powe dissipated in the circuit is
P'=iV0cosα,i=VR
And cosα=V1+VrV0=V1+V2cosϕV0
Solving P'V20+V21−V222R
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - II(H.W)
Explore 13 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - V
Explore 83 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
An AC voltage is applied acrss a series combination of L and R. If the voltage drop across the resistor and inductor are 20V and 15V respectiely, then applied peak voltage is
A25VB35VC25√2VD5√7VIn an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
A√(V1−V2)2+V23B√V21+(V2−V23C√V22+(V1−V3)2DV1+V2+V3A 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is VR=2sin(1000t)V. The voltage across the inductors is
A80sin(1000t+π2)B40sin(1000t+π2)C80sin(1000t−π2)D40sin(1000π−π2)
In an LCR circuit, the voltages across the components are VL,VC and VR respectively. The voltage of source will be -
View SolutionA coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
View SolutionIf V0 and I0 are the peak current and voltage across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
View SolutionA voltmeter of resistance 600Ω when connected in turn across resistances R1 and R2 gives readings of V1 and V2, respectively. If the battery is ideal, then

View SolutionA 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is, VR=(2.0V)sin(103t).
Find amplitude of the voltage across the inductor.
View Solution