If various elements, i.e., resistance capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H respectively. Given emf as, V=100√2sin1000t volts
Voltage across the resistor is
70.7 Volts
100 Volts
141.4 Volts
270.7 Volts
The correct Answer is:A
rms value of voltage across the source
Vrms=100√2√2=100 volt
From question, ω=1000rad/s
irms=Vrms|Z|=Vrms√R2+(XL−XC)2
=Vrms√R2+(ωL−1ωC)2
=100√(1000)2+(1000×2−11000x1×10−6)2
= 0.0707 amp
Since the current will be same every where in the circuit, therefore
P.D acrossresistor
VR=irmsR=0.0707×1000=70.7 volts
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - II(H.W)
Explore 13 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - V
Explore 83 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Find the voltage across the various elements, i.e., resistance, capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0 H respectively . Given emf as,
V = 100sqrt2 sin 1000 t V
View SolutionFind the voltage across the various elements, i.e., resistance, capacitance and inductance which are in series and having values 100Ω,1μF and 2.0H, respectively. Given emf is
V=100√2sin1000t volt
View Solution
Knowledge Check
If various elements, i.e., resistance capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H respectively. Given emf as, V=100√2sin1000t volts
voltage across the inductor isA70.7 VoltsB101 VoltsC141.4 VoltsD270.7 VoltsIf various elements, i.e., resistance capacitance and inductance which are in series and having values 1000Ω,1μF and 2.0H respectively. Given emf as, V=100√2sin1000t volts
voltages across the capacitor isA70.7 VoltsB102 VoltsC141.4 VoltsD270.7 VoltsA 100Ω resistance is connected in series with a 4H inductor. The voltage across the resistor is VR=2sin(1000t)V. The voltage across the inductors is
A80sin(1000t+π2)B40sin(1000t+π2)C80sin(1000t−π2)D40sin(1000π−π2)
Find the potential difference across resistance, capacitance and inductance in series LCR circuit where L=2.0H,C=1μFandR=100Ω. The applied emf has the form V=100√2sin(1000t)
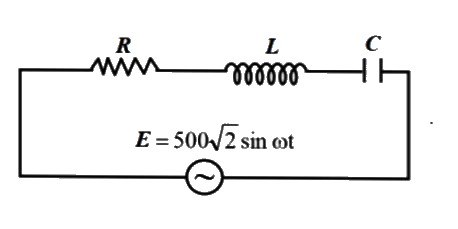
View SolutionIn the series L−C−R circuit shown in the figure, the rms voltage across the resistor and inductor are 400 V and 700 V respectively. If the applied voltage is E=500√2sin(ωt), then the peak voltage across the capacitor is
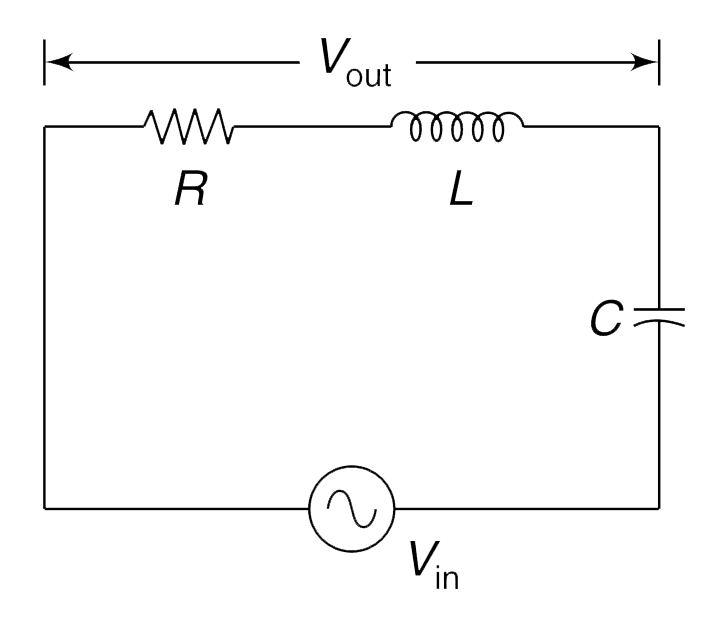
View SolutionA series LCR circuit having resistance R, capacitance C and inductance L has a voltage source of angular frequency ω and voltage V∈. Output voltage (Vout) is taken as voltage across the resistor and inductor combined.
(a) Find η=VoutVin
(b) Find η in the limit of large ω(ω>>1RC,1√LC,RL)
(C )Find η in the limit of smallω(ω>>1RC,1√LC,RL)
View SolutionA resistor of 500Ω and an inductance of 0.5 H are in series with an ac source which is given by V=100√2sin(1000t). The power factor of the combination is
View SolutionAn alternating e.m.f. of 0.1 V is applied across an LCR series circuit having R=2Ω,C=40μFandL=100mH. At resonance, the voltage drop across the inductor is
View Solution

