In the previous problem another block C of mass m is placed at distance 1m right of block B. Find (a) the distance travelled by the combined mass if the collision is completely inelastic and (b) separation between the blocks when they stop after head - on elastic collision.
Speed of block B after traveling a distance 1m.
u21=(2)2−2as=4−2×1×1=2⇒μ1=√2m/s
(a=μg=0.1×10=1m/s2)
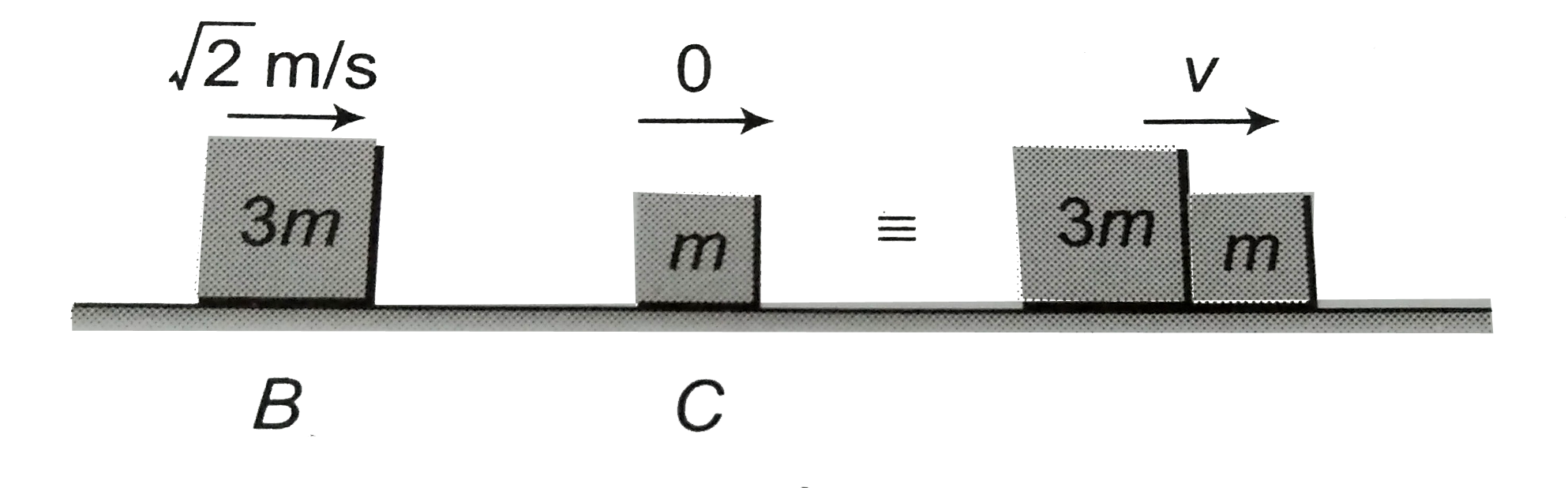
(a) Now , the collision is completely elastic , the blocks move together.
By the momentum conservation
3m√2+m×0=(3m+m)V⇒V=3√24m/s
The distance travelled by the combined mass on a rough surface
0=V2−2ad⇒0=(3√24)2−2×1×d
d=916m
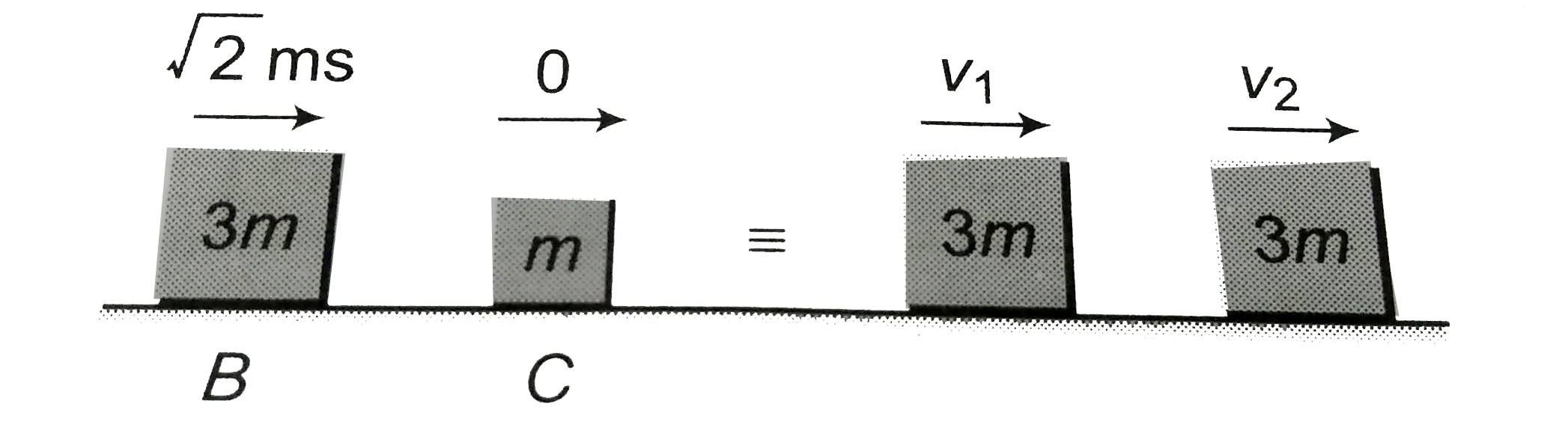
(b) If the collision is head - on elastic , the blocks will move with different velocities
3m√2+m×0=3mv1+mv2 (i)
v1+√2=v2+0 (ii)
Solving , v1=1√2m/s,v2=3√2m/s
Let the distance travelled by blocks B and C are d1 and d2 before stop, in the same direction.
0=v21−2ad
0=12−2×1×d1⇒d1=14m
0=v22−2ad2
0=(3√2)2−2×1×d2
⇒d2=94m
Separation between blocks =d2−d1=94−14=2m




Topper's Solved these Questions
Similar Questions
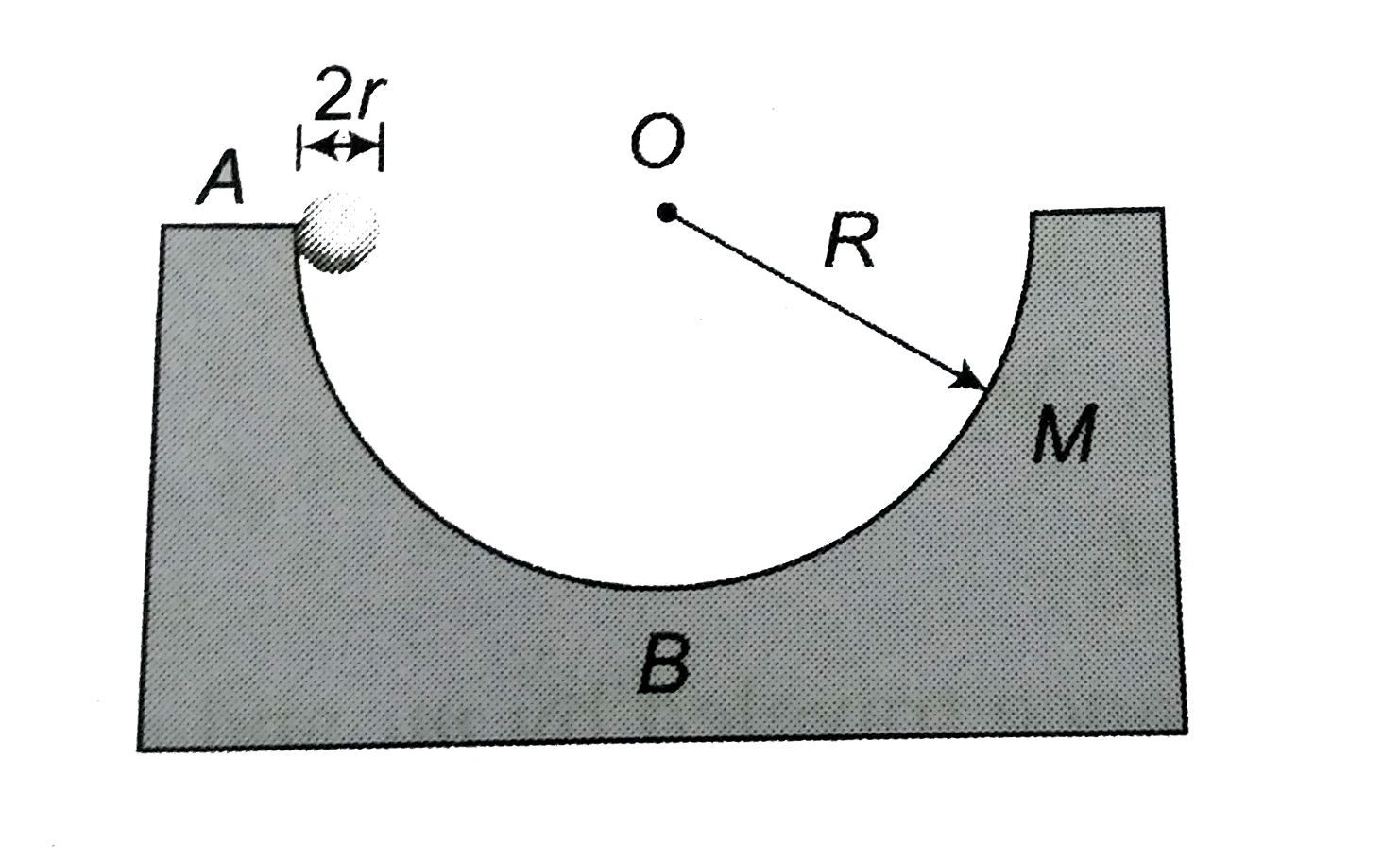
All surfaces are smooth. The ball of mass m is released from A. Find the distance travelled by the block of mass M.
View SolutionA small block of mass M moves with velocity 5 m/s towards an another block of same mass M placed at a distance of 2 m on a rough horizontal surface . Coefficient of friction between the blocks and ground is 0.25 . Collision between the two blocks is elastic , the separation between the blocks , when both of them come to rest , is ( g = 10m/s2)
View Solution
Knowledge Check
In the previous problem , the maximum height attained by the ball and the distance traveled by the block , after collision will be
A2L9,4L9B4L3,L3C4L9,L9DL9,2L9In the previous problem , if the horizontal surface is rough with friction coefficient 0.5 and collision is elastic , head - on , the distance travelled by the block on the rough surface
A5mB10mC15mD20mThe collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
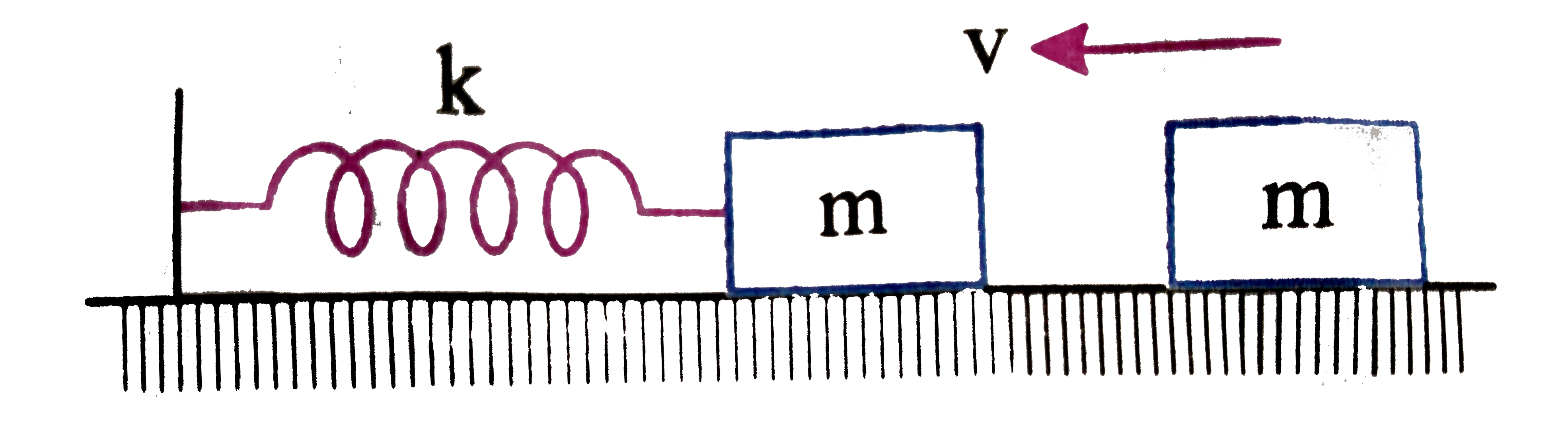 A12mv2Bmv28Cmv24Dmv232
A12mv2Bmv28Cmv24Dmv232
A block 'A' of mass 2m is placed on another block 'B' of mass 4m which in turn is placed on a fixed table. The two blocks have a same length 4d and they are placed as shown in fig The coefficient of friction (both static and kinetic) between the block 'B' and table is μ. There is no friction between the two blocks. A small object of mass m moving horizontally along a line passing through the centre of mass (cm.) of the block B and perpendicular to its face with a speed v collides elastically with the block B at a height d above the table.

(a) What is the minimum value of v(call it v0) required to make the block A topple?
(b) If v=2v0,find the distance (from the point P in the figure ) at which the mass m falls on the table after collision. (Ignore the role of friction during the collision).
View SolutionThe friction coefficient between the horizontal surface and blocks A and B are 115 and 215 respectively. The collision between the blocks is perfectly elastic. Find the separation (in meters) between the two blcoks when they come to rest.

View SolutionThe blocks shown in figure have equal masses. The surface of A is smooth but that of B has a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if a. the collision is perfectly elastic and b. the collision is perfectly inelastic. Take g=10ms2.

View SolutionIn the figure shown, the block A of mass m collides with the identical block B and after collision they stick together. Calculate the amplitude of resulatant vibration.
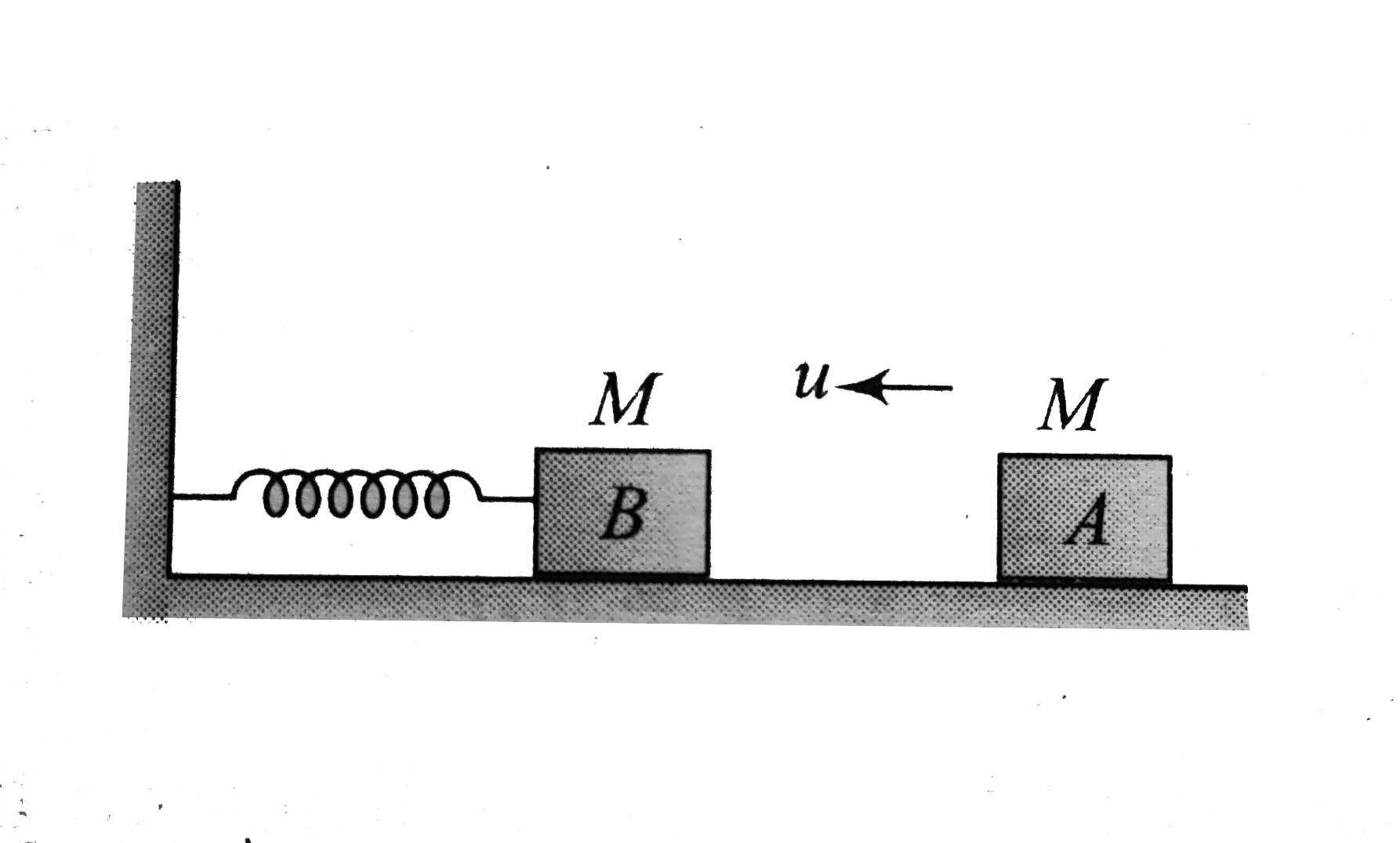
View SolutionA block of mass m moves with a speed v towards the right block which is in equilibrium with a spring attached to rigid wall. If the surface is frictionless and collisions are elastic, the frequency of collisions between the masses will be:
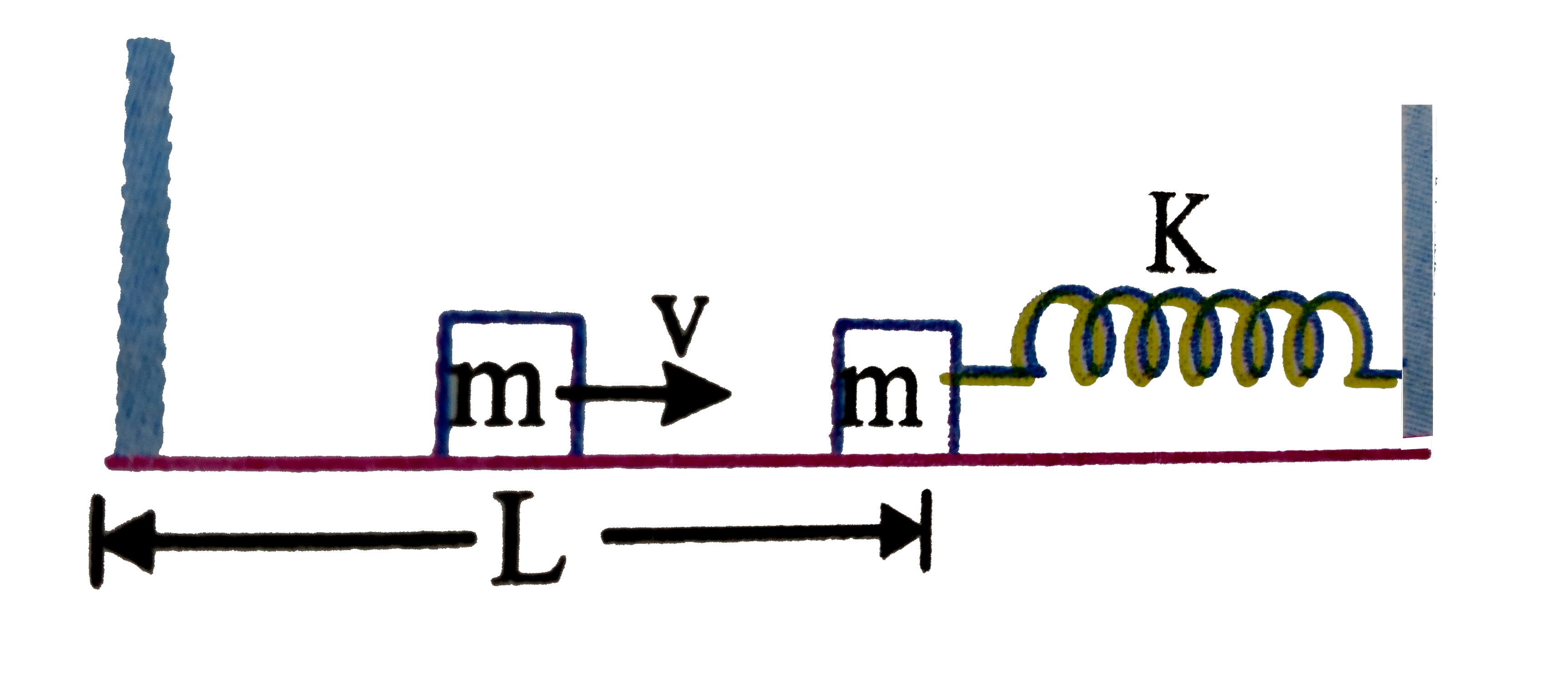
View Solution
