All surfaces are smooth. The ball of mass m is released from A. Find the distance travelled by the block of mass M.
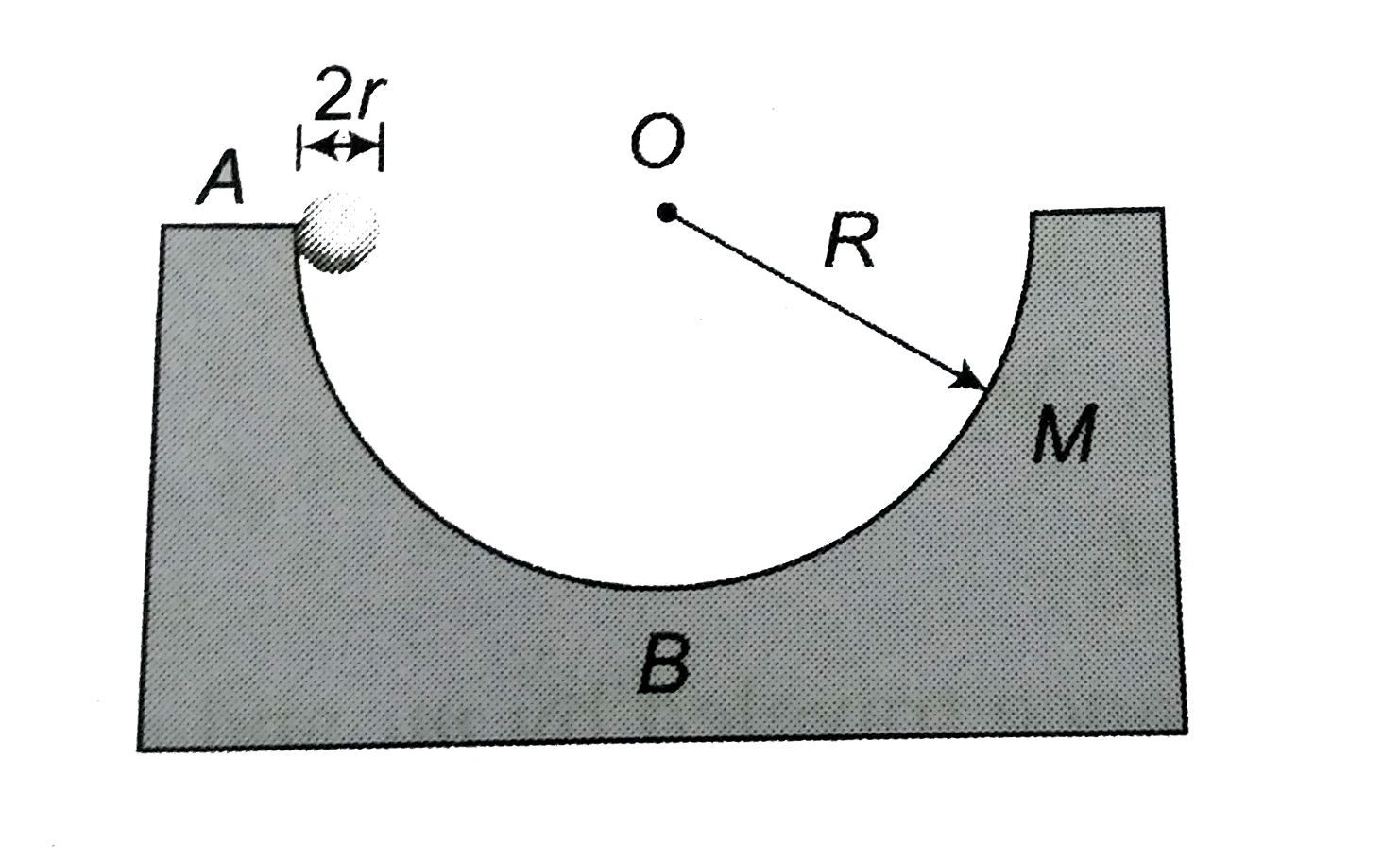
As the external force in the horizontal direction is zero and the system is initially at rest , the horizontal component of c.m. is fixed.
The horizontal distance travelled by the ball towards the right is (R−r).
( When in problems , radius of ball is given , consider it.)
To keep the horizontal component of c.m. fixed (blockofmassM+ballm) has to move towards the left by x.
m(R−r)=(M+m)x
x=m(R−r)M+m
The horizontal distance travelled by the ball relative to the ground is
(R−r)−x=M(R−r)M+m
If the radius of ball is not given
mR=(M+m)x⇒x=mRM+m
Topper's Solved these Questions
Similar Questions
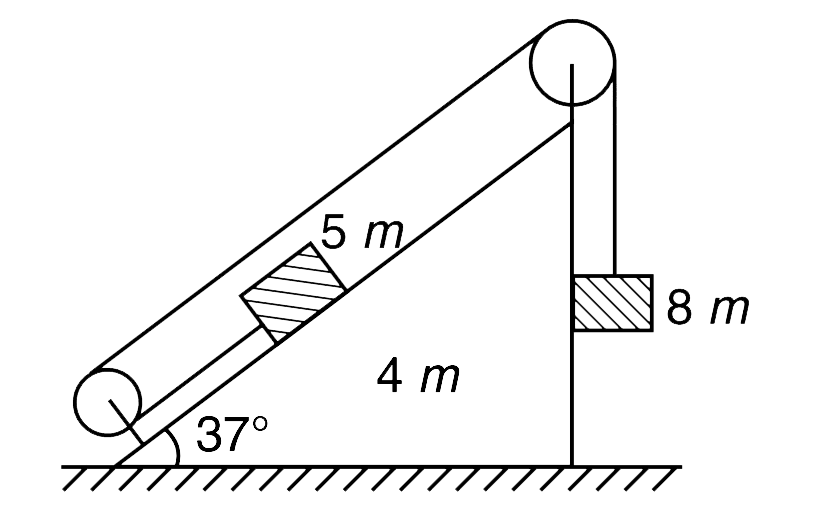
In the system shown in the figure all surfaces are smooth, pulley and string are massless. The string between the two pulleys and between pulley and block of mass 5 m is parallel to the incline surface of the block of mass 4 m. The system is released from rest. Find the acceleration of the block of mass 4 m . [tan37∘=34]
View SolutionA block of mass m is placed on hthe top of bigger wedge M. All the surfaces are frictionless. The system is released from rest. Find the distance moved by smaller block (w.r.t triangular wedge) when bigger wedge travles distance X on plane surface
_PHY_219_Q01.png)
View Solution
Knowledge Check
All surfaces are smooth. The acceleration of mass m relative to the wedge is
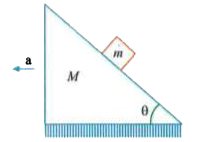AgsinθBgsinθ+acosθCgsinθ−acosθDacosθAll surfaces are smooth The acceleration of mass m relative to the wedge is
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
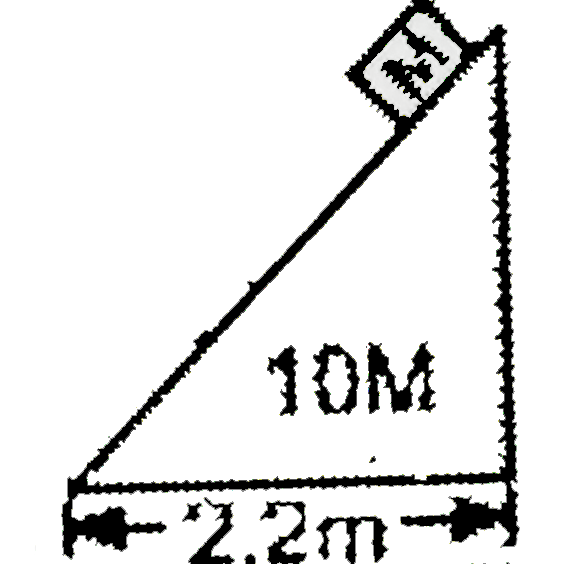A0.22 mB0.20 mCzeroD0.24 m
Inside a smooth spherical shell of the radius R a ball of the same mass is released from the shown position (Fig.) Find the distance travelled by the shell on the horizontal floor when the ball comes to the lowest point of the shell.
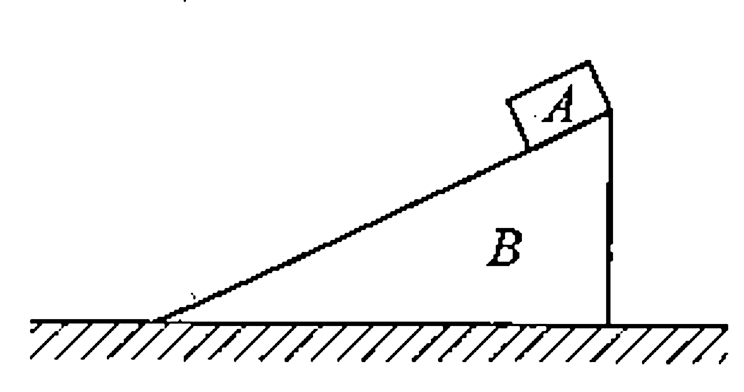
View SolutionA block A (mass 4M) is placed on the top of a wedge block B of base length l (mass=20M) as shown in figure. When the system is released from rest. Find the distance moved by the block B till the block A reaches ground Assume all surfaces are frictionless.
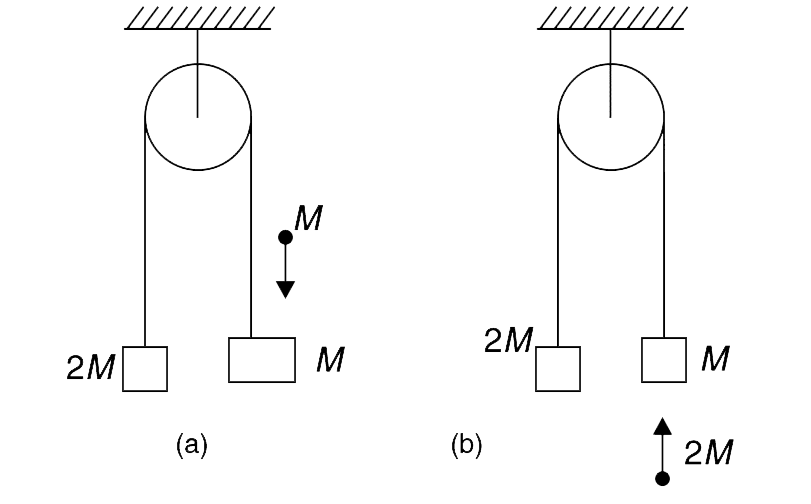
View SolutionTwo blocks of mass M and 2M are connected to the two ends of a light, inextensible string passing over an ideal pulley as shown in figure. The system is released from rest.
(a) One second after the system is released, a particle of mass M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling downward. Find the total distance travelled by block of mass 2M after it is released.
(b) One second after the system is released, a particle of mass 2M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling in upward direction. Find distance travelled by the block of mass 2M after it is released to the time it comes to rest for the first time (g=10m/s)2
View SolutionA particle A of mass m is situated at highest point of wedge B of mass 2m is released from rest. Then distance travelled by wedge B( with respect to ground ) when particle A reaches at lowest position. Assume all surfaces are smooth.
View SolutionA smooth wedge of mass M is pulled towards left with an acceleration a=gcotθ on a horizontal surface and a block of mass m is released w.r.t. wedge. Then answer the following
Time taken by the block to reach the ground is
View Solution