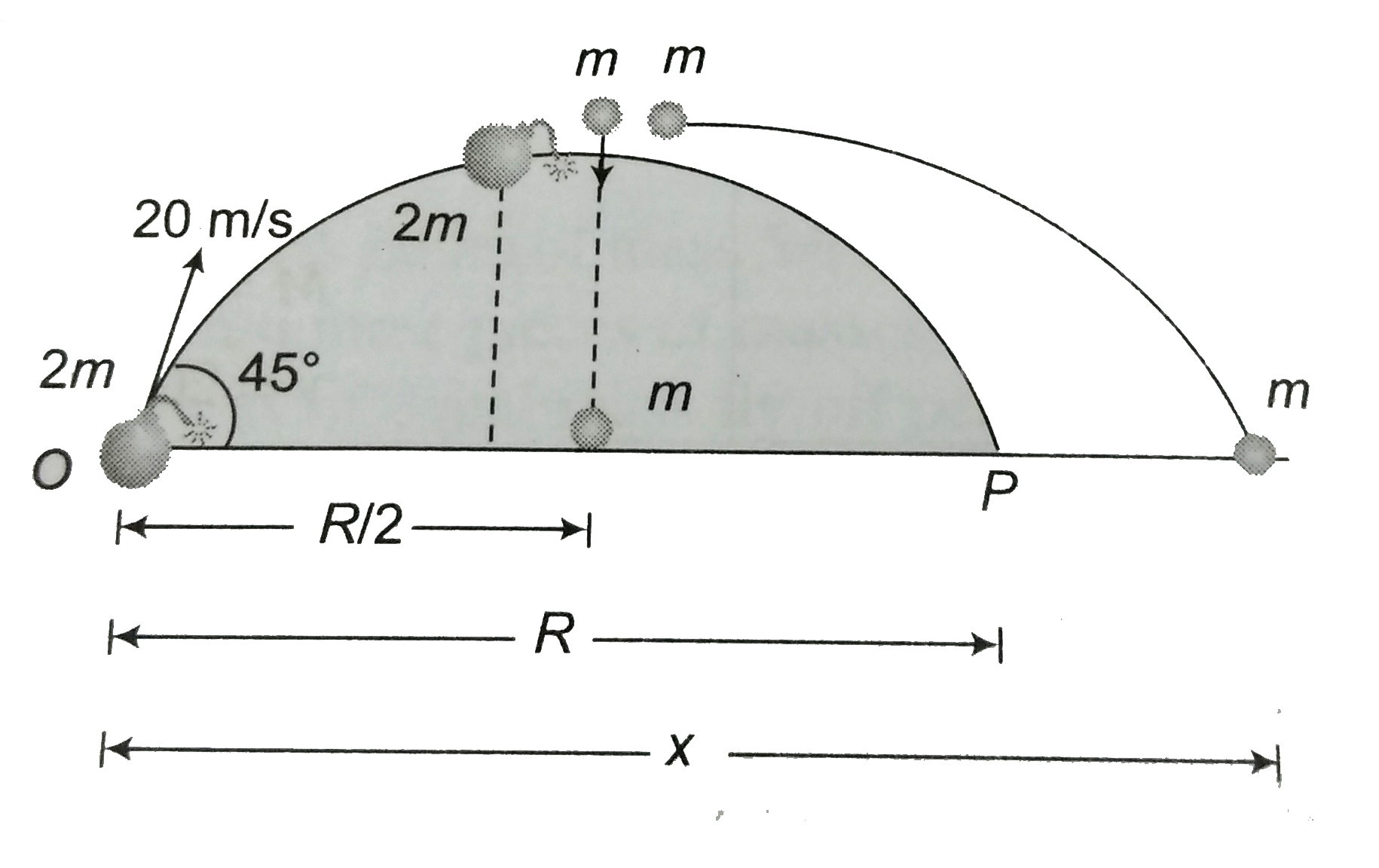
A bomb is thrown at a speed at an angle . At the highest point , it explodes into two parts of equal mass , the one part coming to rest. Find the distance from the origin to the point where the other part strikes the ground.
The center of mass will hit the ground at
Topper's Solved these Questions
Similar Questions
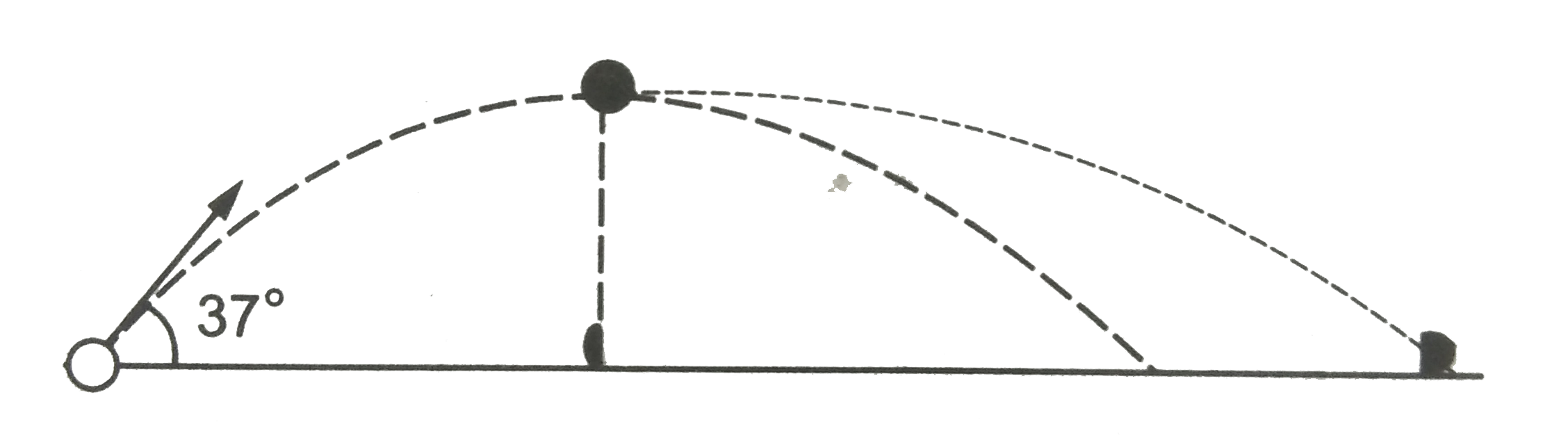
A projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.
View SolutionA body is projected with a speed 160 m/s at an angle 53∘ with the horizontal, At the highest point, body explodes into two pieces with mass ratio 1:3. Smaller piece comes to rest immediately after explosion. Find the distance of point from point of projection where heavier piece strikes the horizontal surface.
View Solution
Knowledge Check
In the previous problem , if a bomb explodes into three parts of mass ratio 1:1:2 , one smaller part retraces its path, the second smaller part coming to rest, the distance from the point of projection , where the heavier part strikes the ground is
A75mB95mC105mD120mA projectile of mass 20 kg is fired with a velocity of 400m/sat an angle of 45∘ with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
A24000 mB16000 mC32000 mD8000 mA bomb of mass m is projected from the ground with speed v at angle θ with the horizontal. At the maximum height from the ground it explodes into two fragments of equal mass. If one fragment comes to rest immediately after explosion, then the horizontal range of centre of mass is
Av2sin2θgBv2sinθgCv2sinθ2gDv2sin2θg
A projectile of mass "m" is projected from ground1 with a speed of 50 m/s at an angle of 53∘ with the horizontal. It breaks up into two equal parts at the highest point of the trajectory. One particle coming to rest immediately after the explosion.
The distance between the pieces of the projectile when they reach the ground are :
View SolutionA projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)
View SolutionA particle is projected such that its horizontal range would be R. At the highest point, the particle breaks into two identical parts P and Q. If P comes to rest, the horizontal distance of point from the point of projection (i.e. origin) where the particle Q lands on the ground is
View SolutionA palm tree 90 ft high, is broken by the wind and its upper part meet the ground at an angle of 30∘. Find the distance of the point where the top of the tree meets the ground from its root:
View SolutionA bomb of mass 4m, while moving on a parabolic path, explodes at highest point of its path. If breaks into two parts of mass ratio 1:3, smaller part coming to rest. The range of this projectile was 60m in the absence of explosion. The distance of the second part from the point of projection when it strikes the ground is
View Solution
