An iron sphere of mass 100kg is suspended freely from a rigid support by means of a rope of length 2m.The horizontal force required to displace it horizontally through 50cm is nearly
980N
490N
245N
112.5N
The correct Answer is:C
To solve the problem of finding the horizontal force required to displace an iron sphere of mass 100 kg horizontally by 50 cm when suspended from a rope of length 2 m, we can follow these steps:
Step 1: Understand the Setup
The iron sphere is suspended from a rigid support by a rope. When a horizontal force F is applied, the sphere is displaced horizontally by 50 cm. The rope forms an angle θ with the vertical.
Step 2: Draw a Diagram
Draw a diagram showing the sphere, the rope, and the horizontal displacement. Label the following:
- Length of the rope L=2m
- Vertical displacement y=L−√L2−(0.5)2
- Horizontal displacement x=0.5m
Step 3: Calculate the Angle θ
Using the sine function, we can find the angle θ:
sinθ=xL=0.52=14
Thus, θ=sin−1(14).
Step 4: Resolve Forces
At equilibrium, the forces acting on the sphere can be resolved into two components:
- Vertical component: Tcosθ=mg
- Horizontal component: F=Tsinθ
Where:
- T is the tension in the rope,
- m=100kg (mass of the sphere),
- g=9.81m/s2 (acceleration due to gravity).
Step 5: Calculate the Weight of the Sphere
Calculate the weight mg:
mg=100kg×9.81m/s2=981N
Step 6: Relate the Forces
From the vertical component:
Tcosθ=981N(1)
From the horizontal component:
F=Tsinθ(2)
Step 7: Divide the Two Equations
Dividing equation (2) by equation (1):
FTcosθ=TsinθTcosθ
This simplifies to:
F=mgtanθ
Step 8: Calculate tanθ
Using the identity tanθ=sinθcosθ:
sinθ=14
Using Pythagorean theorem:
cosθ=√1−sin2θ=√1−(14)2=√1−116=√1516=√154
Thus:
tanθ=sinθcosθ=14√154=1√15
Step 9: Substitute Back to Find F
Now substitute tanθ back into the equation for F:
F=mgtanθ=981×1√15
Step 10: Calculate the Final Value
Calculating F:
F≈981×0.2582≈253.5N
Conclusion
The horizontal force required to displace the sphere horizontally through 50 cm is approximately 250 N.
The iron sphere is suspended from a rigid support by a rope. When a horizontal force F is applied, the sphere is displaced horizontally by 50 cm. The rope forms an angle θ with the vertical.
Draw a diagram showing the sphere, the rope, and the horizontal displacement. Label the following:
- Length of the rope L=2m
- Vertical displacement y=L−√L2−(0.5)2
- Horizontal displacement x=0.5m
Using the sine function, we can find the angle θ:
sinθ=xL=0.52=14
Thus, θ=sin−1(14).
At equilibrium, the forces acting on the sphere can be resolved into two components:
- Vertical component: Tcosθ=mg
- Horizontal component: F=Tsinθ
- T is the tension in the rope,
- m=100kg (mass of the sphere),
- g=9.81m/s2 (acceleration due to gravity).
Calculate the weight mg:
mg=100kg×9.81m/s2=981N
From the vertical component:
Tcosθ=981N(1)
From the horizontal component:
F=Tsinθ(2)
Dividing equation (2) by equation (1):
FTcosθ=TsinθTcosθ
This simplifies to:
F=mgtanθ
Using the identity tanθ=sinθcosθ:
sinθ=14
Using Pythagorean theorem:
cosθ=√1−sin2θ=√1−(14)2=√1−116=√1516=√154
Thus:
tanθ=sinθcosθ=14√154=1√15
Now substitute tanθ back into the equation for F:
F=mgtanθ=981×1√15
Calculating F:
F≈981×0.2582≈253.5N
The horizontal force required to displace the sphere horizontally through 50 cm is approximately 250 N.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-III(C.W)
48 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. SINGLE ANS.
8 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-I(C.W)
43 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
Knowledge Check
A 10kg body is suspended by a rope is pulled by means of a horizontal force to make 60∘ by rope to vertical.The horizontal forces is
A10kgwtB30kgwtC10√3kgwtD30√3kgwtA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
AMg√2BMg(√2−1)CMg(√2+1)DMg√2A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
AMg(√2+1)BMg√2CMg√2DMg(√2−1)
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle 45∘ with the initial vertical direction is
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
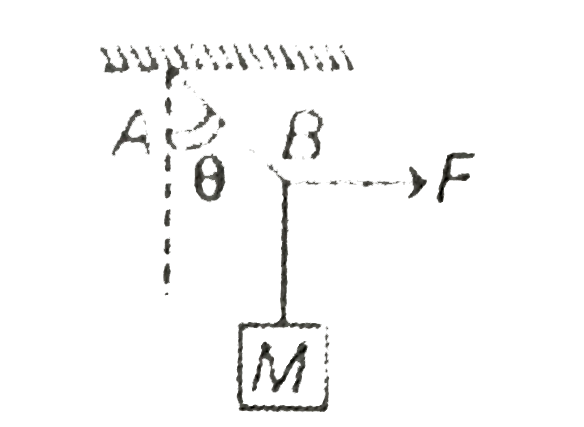
View SolutionA roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
View Solution