The displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward quarter revolution where perimeter of the wheel is 4πm, is (Assume the forward direction as x-axis)
√(π+2)2+4along tan−12π with x-axis
√(π+2)2+4along tan−12π−2 with x-axis
√(π+2)2+4along tan−12π with x-axis
√(π+2)2+4along tan−12π−2 with x-axis
The correct Answer is:B
To solve the problem, we need to determine the displacement of a point on the wheel that is initially in contact with the ground after the wheel rolls forward by a quarter revolution. Given that the perimeter of the wheel is 4π meters, we can follow these steps:
Step 1: Calculate the radius of the wheel
The perimeter (circumference) of the wheel is given by the formula:
Perimeter=2πR
where R is the radius of the wheel. We know the perimeter is 4π meters, so we can set up the equation:
2πR=4π
Dividing both sides by 2π:
R=2 meters
Step 2: Determine the distance traveled during a quarter revolution
A quarter revolution corresponds to 90∘ of rotation. The distance traveled by the wheel in this case is:
Distance=14×Perimeter=14×4π=π meters
Step 3: Analyze the position of the point after rolling
Initially, the point in contact with the ground is at the bottom of the wheel. After rolling forward by a quarter revolution, this point will move to the right by π meters along the x-axis and will also rise to a height equal to the diameter of the wheel (which is 2R=4 meters) because it moves from the bottom to the top of the wheel.
Step 4: Determine the coordinates of the point after rolling
Initially, the point is at the coordinates (0,0). After rolling forward by π meters, the new coordinates of the point will be:
New position=(π,4)
Step 5: Calculate the displacement
Displacement is the straight-line distance from the initial position to the final position. The initial position is (0,0) and the final position is (π,4). The displacement can be calculated using the Pythagorean theorem:
Displacement=√(Δx)2+(Δy)2=√(π−0)2+(4−0)2=√π2+16
Final Answer
The displacement of the point of the wheel after rolling forward by a quarter revolution is:
√π2+16 meters
---
The perimeter (circumference) of the wheel is given by the formula:
Perimeter=2πR
where R is the radius of the wheel. We know the perimeter is 4π meters, so we can set up the equation:
2πR=4π
Dividing both sides by 2π:
R=2 meters
A quarter revolution corresponds to 90∘ of rotation. The distance traveled by the wheel in this case is:
Distance=14×Perimeter=14×4π=π meters
Initially, the point in contact with the ground is at the bottom of the wheel. After rolling forward by a quarter revolution, this point will move to the right by π meters along the x-axis and will also rise to a height equal to the diameter of the wheel (which is 2R=4 meters) because it moves from the bottom to the top of the wheel.
Initially, the point is at the coordinates (0,0). After rolling forward by π meters, the new coordinates of the point will be:
New position=(π,4)
Displacement is the straight-line distance from the initial position to the final position. The initial position is (0,0) and the final position is (π,4). The displacement can be calculated using the Pythagorean theorem:
Displacement=√(Δx)2+(Δy)2=√(π−0)2+(4−0)2=√π2+16
The displacement of the point of the wheel after rolling forward by a quarter revolution is:
√π2+16 meters
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-III(C.W)
48 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. SINGLE ANS.
8 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-I(C.W)
43 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution? Take the radius of the wheel as R and the x-axis as the forward direction?
View SolutionA wheel of circumference C is at rest on the ground. When the wheel rolls forward through half a revolution, then the displacement of initial point of contact will be
View Solution
Knowledge Check
Assertion : The total displacement moved by a point located on the periphery of a wheel of radius R in one revolution is 2πR. Wheel is rolling.
Reason : In rolling motion of a wheel, every point on its periphery comes in contact with the surface once in one revolution.ABoth Assertion & Reason are true & the Reason is a correct explanation of the Assertion.BBoth Assertion and Reason are true but Reason is not a correct explanation of the Assertion.CAssertion is true but the Reason is false.DBoth Assertion & Reason are false.A wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
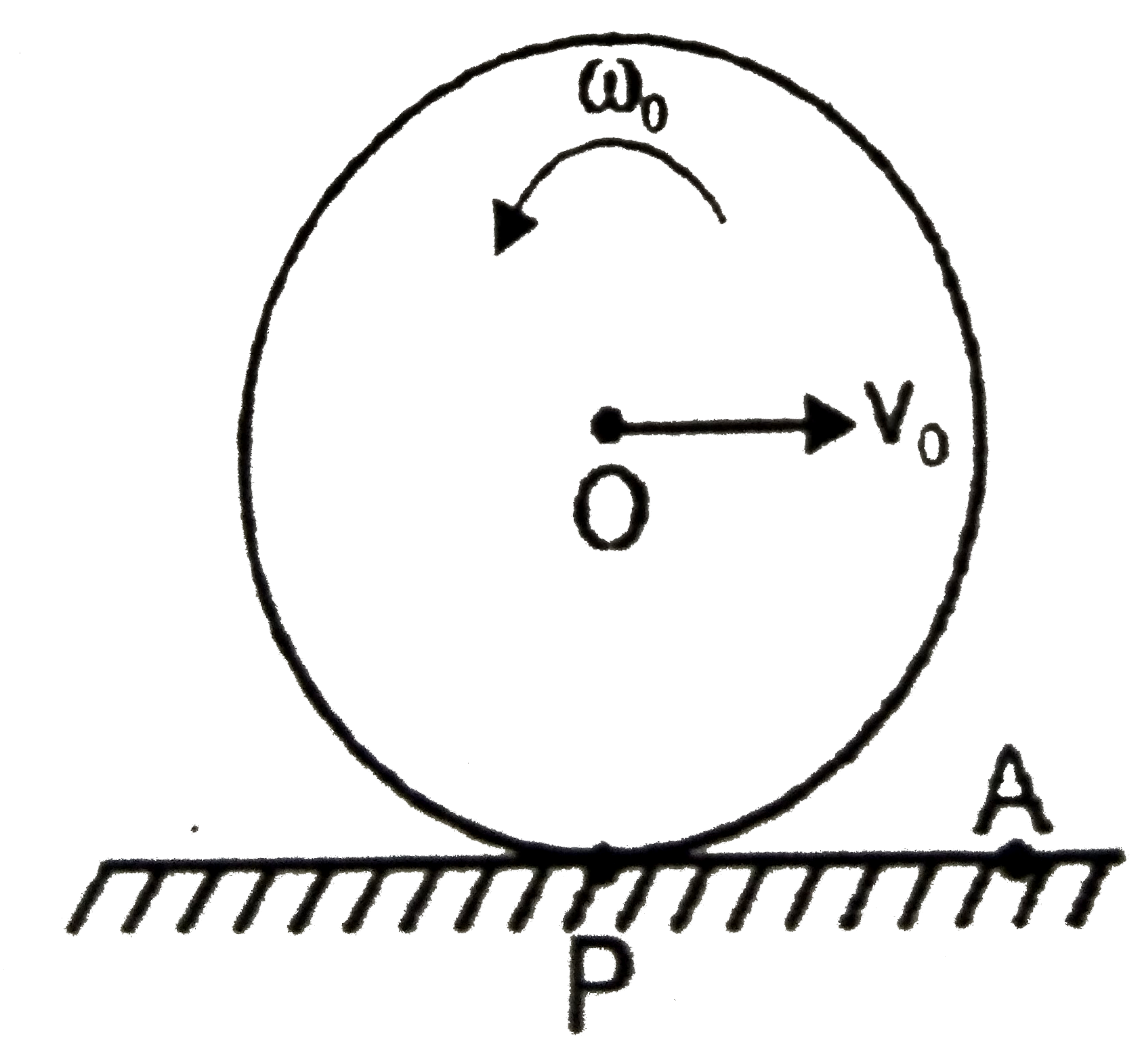
If the wheel comes to permanent rest after sometimes, then :Av0=ω0rBv0=ω0k2rCv0=ω0r2RDV0=ω0(r+k2r)A wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
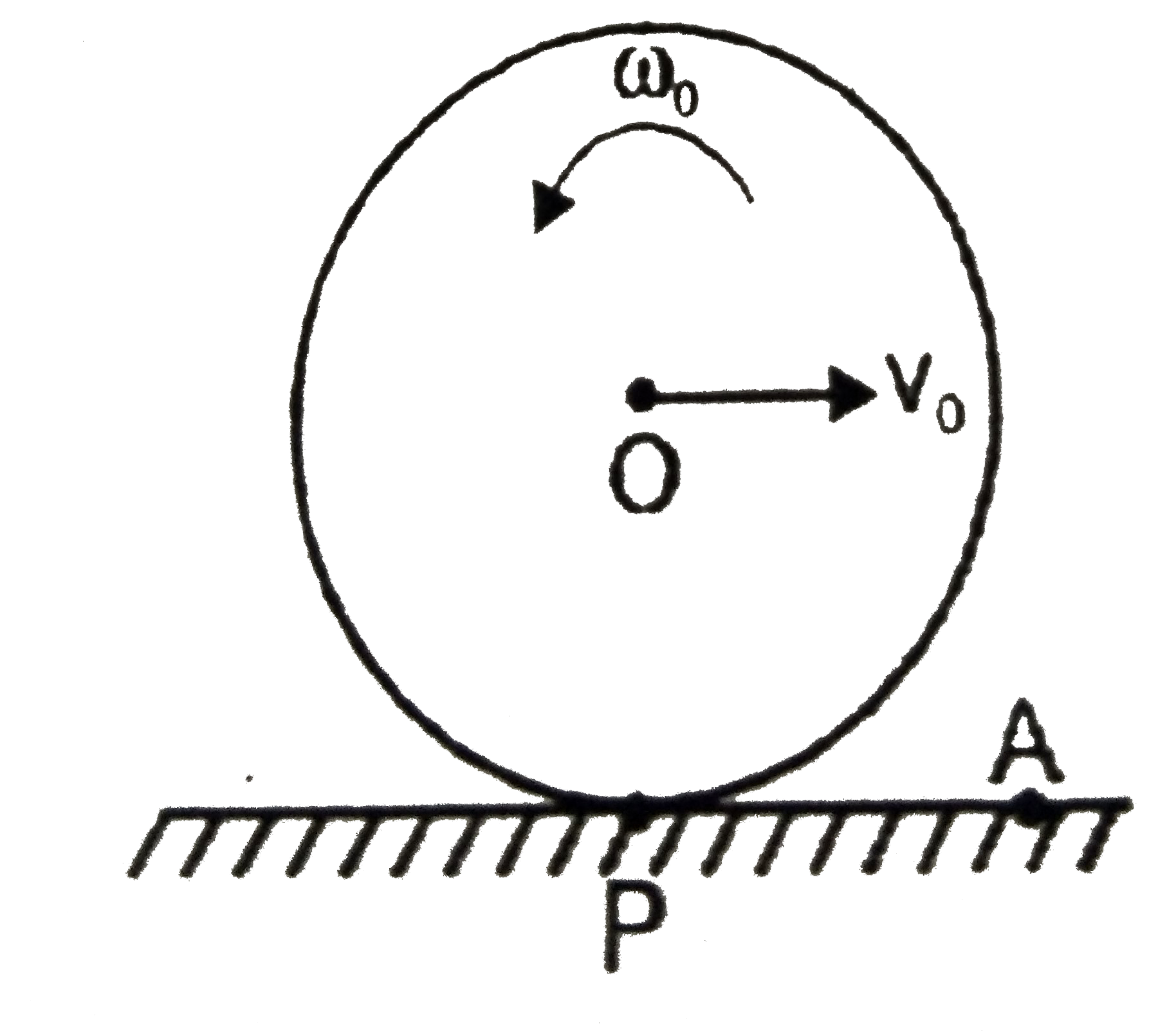
If above question , distance travelled by centre of mass of the wheel before it stops is −Av202μg(1+r2k2)Bv202μgCv202μg(1+k2r2)DNone of these
If a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

View SolutionThe fore wheel of a carriage makes 6 revolutions more than the rear wheel in going 120m. If the diameter of the fore wheel be increased by 14 its present diameter and the diameter of the rear wheel be increased by one-fifth of its present diameter, then the fore wheel makes 4 revolutions more than the rear wheel in going the same distance. Find the circumference of each wheel of the carriage.
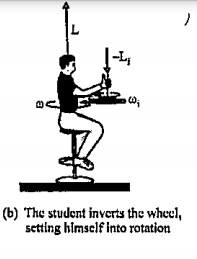
View SolutionFigure shows a student, sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose moment of inertia is I about its central axis. The wheel is rotating at an angular speed ωi from an overead perspective, the rotation is counter clockwise. The axis of the wheel point vertical, and the angular momentum →Li of the wheel points vertically upward. The student now inverts the wheel, as a result, the student and stool rotate about the stool axis. With what angular speed and direction does the student then rotate? (The moment of inertia of the student+stool+wheel system about the stool axis is I0)

View SolutionThe square of angular velocity ω of a certain wheel increases linearly with the angular displacement θ during 100 revolutions of the wheel's motion as shown in the figure. The time t required for given 100 revolutions is 10mπn. Find (m+n).
'(##CEN_KSR_PHY_JEE_C07_028_Q17##)'
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
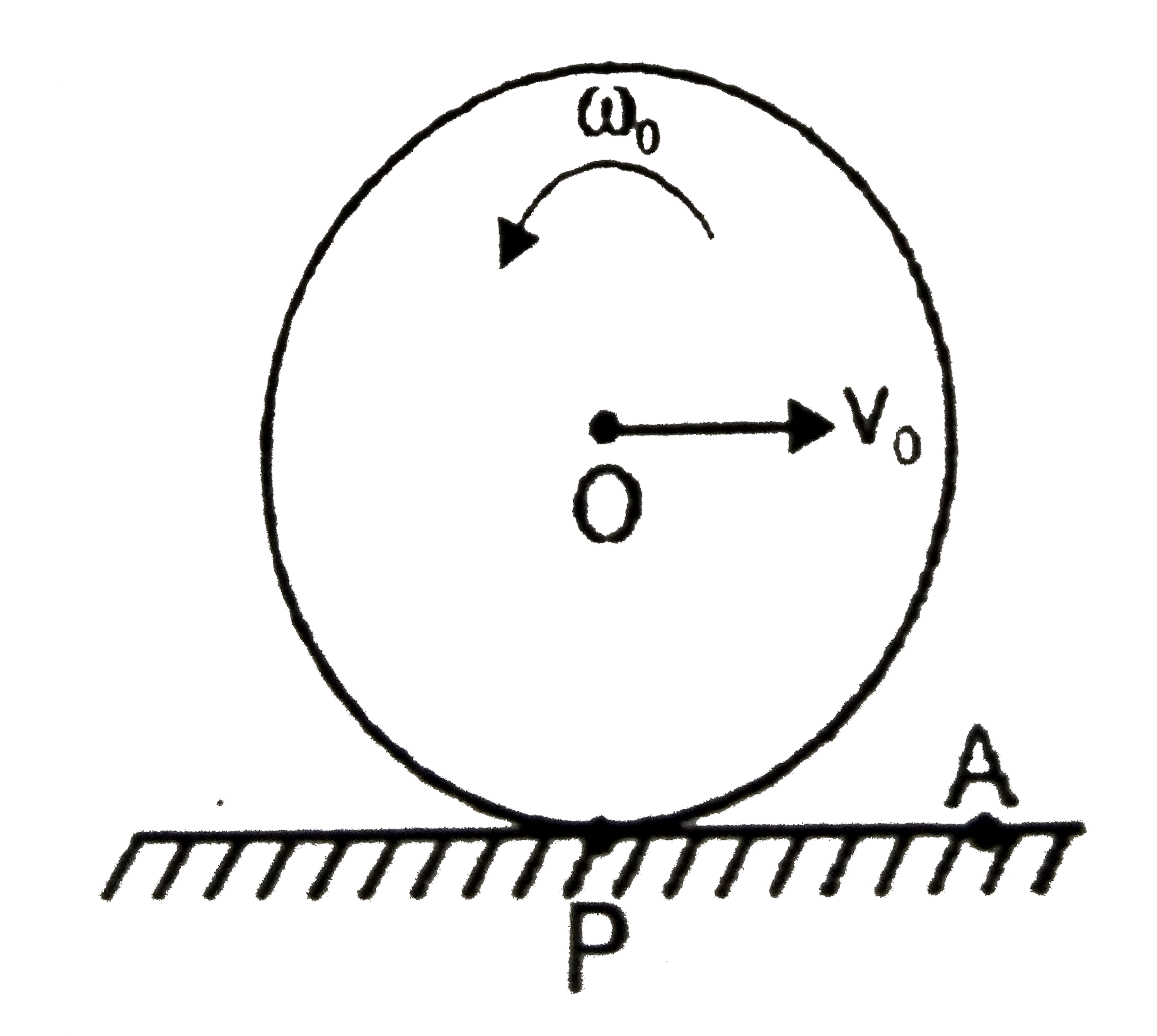
Which of the following is conserved ?
View Solution
