From a point on the ground a particle is projected with initial velocity u,such that its horizontal range is maximum. The magnitude of average velocity during its ascent.
√5u2√2
5u4
√32√2
None
The correct Answer is:A
To solve the problem, we need to find the magnitude of the average velocity during the ascent of a projectile that is projected with an initial velocity u for maximum horizontal range.
1. Understanding Maximum Range:
- The horizontal range R of a projectile is maximized when the angle of projection θ is 45∘.
- The formula for maximum range is given by:
Rmax=u2sin2θg
- For θ=45∘, sin90∘=1, thus:
Rmax=u2g
2. Finding the Displacement During Ascent:
- The maximum height h reached by the projectile can be calculated using:
h=u2sin2θ2g
- For θ=45∘:
h=u2(1√2)22g=u2⋅122g=u24g
3. Calculating the Horizontal Displacement:
- The horizontal displacement at the peak (point P) during ascent is half of the maximum range:
x=Rmax2=u22g
4. Finding the Total Displacement:
- The total displacement d from the point of projection to point P (the peak) can be calculated using the Pythagorean theorem:
d=√x2+h2
- Substituting the values:
d=√(u22g)2+(u24g)2
- Simplifying:
d=√u44g2+u416g2=√4u4+u416g2=√5u416g2=u2√54g
5. Finding the Time of Ascent:
- The time taken to reach the maximum height can be calculated using:
t=usinθg=u⋅1√2g=u√2g
6. Calculating Average Velocity:
- The average velocity Vavg during ascent is given by:
Vavg=DisplacementTime=dt
- Substituting the values:
Vavg=u2√54gu√2g=u2√54g⋅√2gu=u√104
Final Answer:
Thus, the magnitude of the average velocity during ascent is:
Vavg=u√104 m/s
- The horizontal range R of a projectile is maximized when the angle of projection θ is 45∘.
- The formula for maximum range is given by:
Rmax=u2sin2θg
- For θ=45∘, sin90∘=1, thus:
Rmax=u2g
- The maximum height h reached by the projectile can be calculated using:
h=u2sin2θ2g
- For θ=45∘:
h=u2(1√2)22g=u2⋅122g=u24g
- The horizontal displacement at the peak (point P) during ascent is half of the maximum range:
x=Rmax2=u22g
- The total displacement d from the point of projection to point P (the peak) can be calculated using the Pythagorean theorem:
d=√x2+h2
- Substituting the values:
d=√(u22g)2+(u24g)2
- Simplifying:
d=√u44g2+u416g2=√4u4+u416g2=√5u416g2=u2√54g
- The time taken to reach the maximum height can be calculated using:
t=usinθg=u⋅1√2g=u√2g
- The average velocity Vavg during ascent is given by:
Vavg=DisplacementTime=dt
- Substituting the values:
Vavg=u2√54gu√2g=u2√54g⋅√2gu=u√104
Thus, the magnitude of the average velocity during ascent is:
Vavg=u√104 m/s
Topper's Solved these Questions
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(C.W)
Explore 45 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-III(C.W)
Explore 48 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:C.U.Q
Explore 36 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
Similar Questions
Knowledge Check
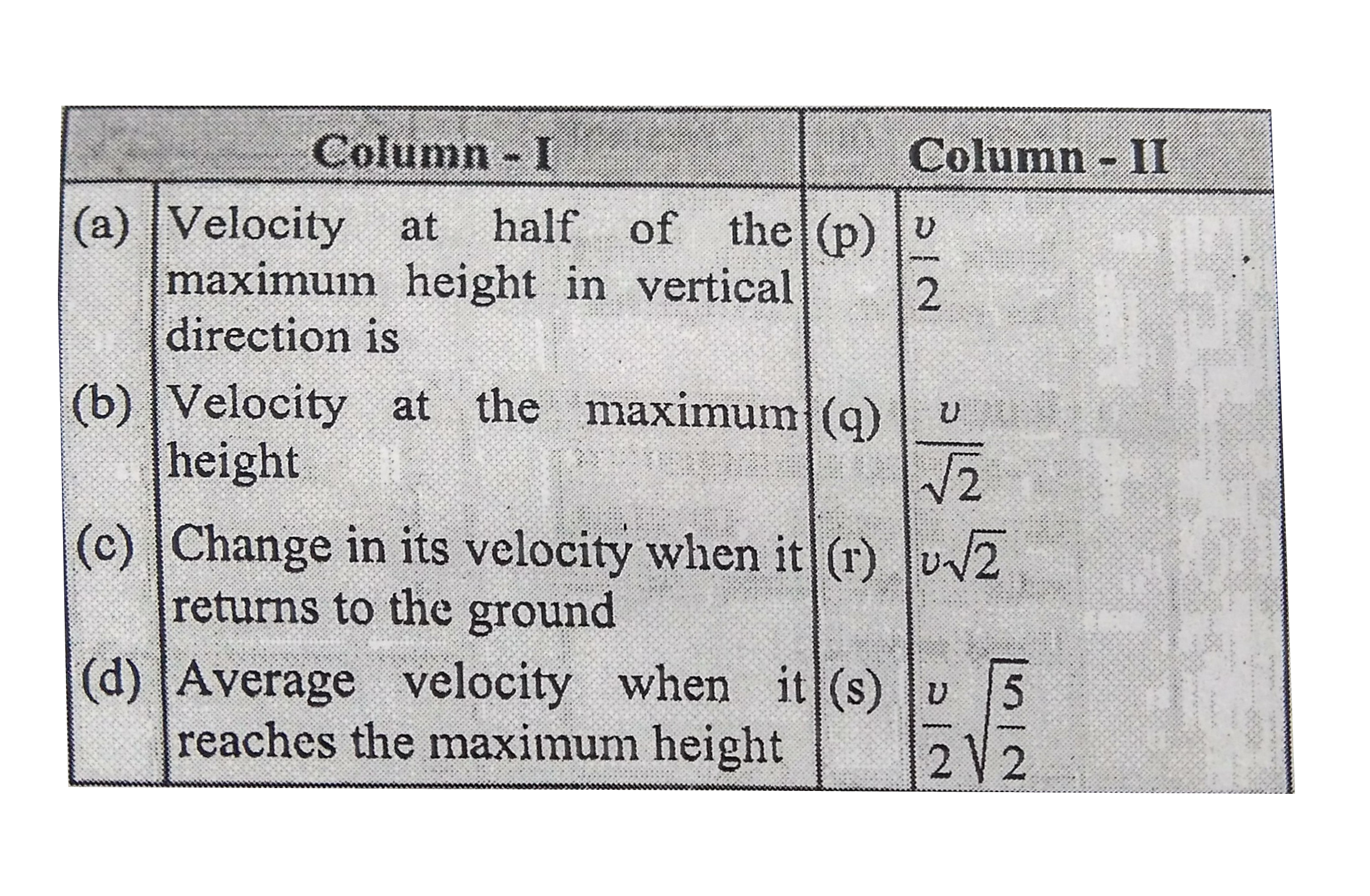
A ball is projected from the ground with velocity u such that its range is maximum Then
AIts velocity at half the maximum height is √32uBIts velocity at the maximum height is uCChange in its velocity when it returns to the ground is uDall the above are trueA body is projected with velocity u such that in horizontal range and maximum vertical heights are samek.The maximum height is
Au22gB3u24gC16u217gD8u217gA particle projected with velocity u at angle θ with horizontal at t=0. What is the magnitude of change in the velocity of the particle when it is at maximum height?
Aucosθ2BucosθCusinθDnone of these
A particle is projected with a velcity (u) so that its horizontal range isthrice the greatest heitht attained. What is its horizontal range?
View SolutionA particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA projectile is fired with a velocity u in such a way that its horizontal range is three times the maximum height aatained . Find the value of horizontal range .
View SolutionA body is projected vertically upwards with a speed v0. Find the magnitude of time average velocity of the body during its ascent.
View SolutionA particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
View Solution