Question

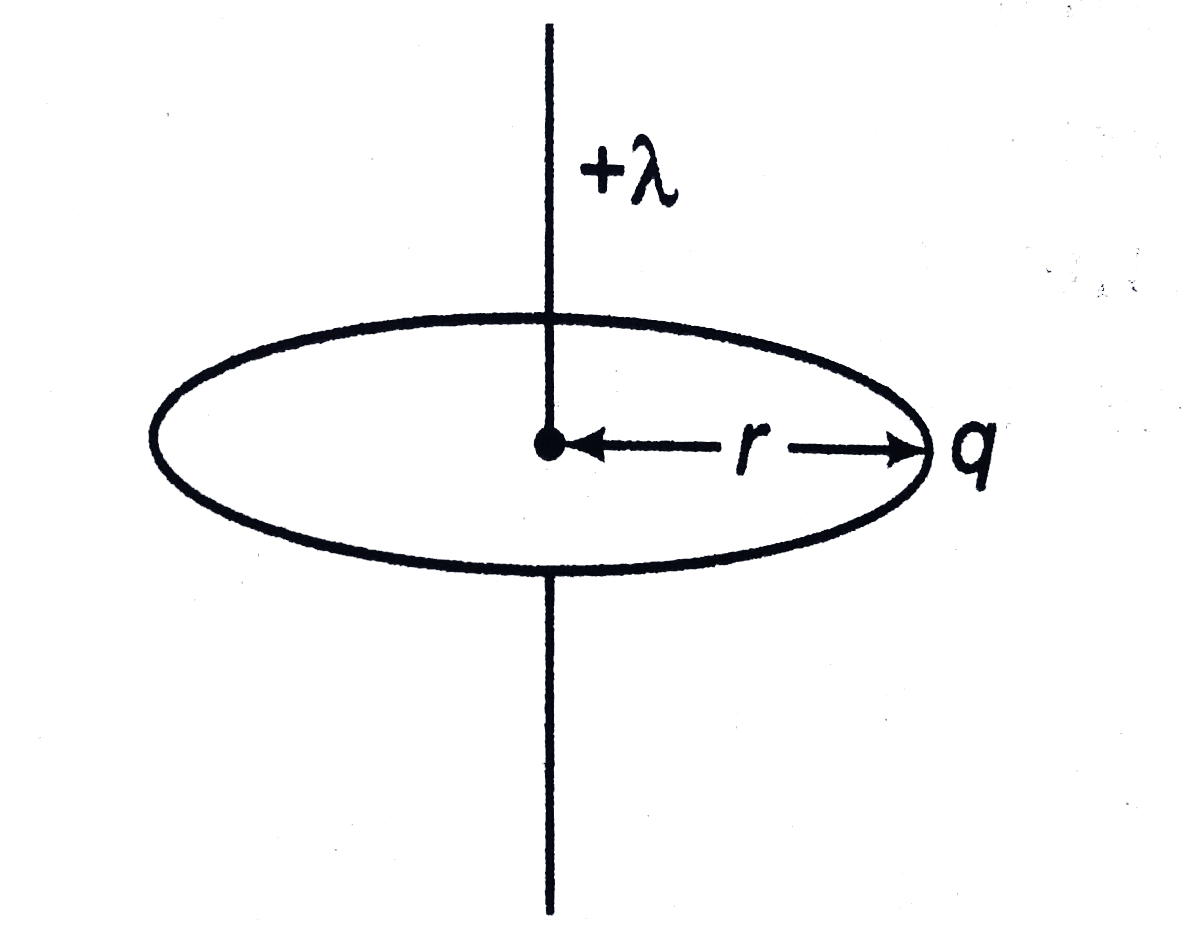
A charge moves with a speed $v$ in a circular path of radius $r$ around a long uniformly charged conductor.

Options

A. `v prop r`
B. `v prop (1)/(r )`
C. `v prop (1)/(sqrt(r ))`
D. `v prop r^(0)`

Answer

4

Explanation

To solve the problem of how the velocity $$v$$ of a charge moving in a circular path around a long uniformly charged conductor depends on the radius $$r$$, we can follow these steps:

1. Identify the Forces Acting on the Charge:
The charge \( q \) moving in a circular path experiences a centripetal force that is provided by the electric force due to the uniformly charged conductor.

2. Centripetal Force Equation:
The centripetal force required to keep the charge moving in a circular path is given by:
\( F_c = \frac{mv^2}{r} \)
where \( m \) is the mass of the charge and \( v \) is its speed.

3. Electric Field Due to the Charged Conductor:
The electric field \( E \) at a distance \( r \) from a long uniformly charged conductor with linear charge density \( \lambda \) is given by:
\( E = \frac{\lambda}{2 \pi \epsilon_0 r} \)
where \( \epsilon_0 \) is the permittivity of free space.

4. Electric Force on the Charge:
The electric force \( F_e \) acting on the charge \( q \) due to the electric field is:
\( F_e = qE = q \left(\frac{\lambda}{2 \pi \epsilon_0 r}\right) \)

5. Set the Forces Equal:
For circular motion, the centripetal force is provided by the electric force:
\( \frac{mv^2}{r} = q \left(\frac{\lambda}{2 \pi \epsilon_0 r}\right) \)

6. Simplify the Equation:
Multiplying both sides by \( r \) gives:
\( mv^2 = q \left(\frac{\lambda}{2 \pi \epsilon_0}\right) \)

7. Solve for \( v^2 \):
Rearranging the equation to isolate \( v^2 \):
\( v^2 = \frac{q \lambda}{2 \pi \epsilon_0 m} \)

8. Conclusion about the Dependence of \( v \) on \( r \):
Notice that in the equation for \( v^2 \), there is no \( r \) term present. This indicates that the speed \( v \) does not depend on the radius \( r \) of the circular path.

9. Final Expression for \( v \):
Taking the square root gives:
\( v = \sqrt{\frac{q \lambda}{2 \pi \epsilon_0 m}} \)
Thus, \( v \) is independent of \( r \).

Final Answer:
The speed \( v \) of the charge moving in a circular path around a long uniformly charged conductor does not depend on the radius \( r \).