A solid sphere of radius $R_{1}$ and volume charge density $ρ = \frac{ρ_{0}}{r}$ is enclosed by a hollow sphere of radius $R_{2}$ with negative surface charge density $σ$ , such that the total charge in the system is zero . $ρ_{0}$ is positive constant and $r$ is the distance from the centre of the sphere . The ratio $R_{2} / R_{1}$ is

A

$\frac{σ}{ρ_{0}}$

B

$\sqrt{\frac{2 σ}{ρ_{0}}}$

C

$\sqrt{\frac{ρ_{0}}{2 σ}}$

D

$\frac{ρ_{0}}{σ}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:3

To find the ratio $\frac{R_{2}}{R_{1}}$ for the given problem, we need to calculate the total charge of both the solid sphere and the hollow sphere and set their sum to zero.
Step 1: Calculate the charge of the solid sphere
The volume charge density of the solid sphere is given by:
$ρ = \frac{ρ_{0}}{r}$
To find the total charge $Q_{1}$ of the solid sphere, we will integrate the charge density over the volume of the sphere.
The differential charge $d q$ in a thin shell of radius $r$ and thickness $d r$ is:
$d q = ρ \cdot d V = ρ \cdot (4 π r^{2} d r) = \frac{ρ_{0}}{r} \cdot (4 π r^{2} d r) = 4 π ρ_{0} r d r$
Now, we integrate $d q$ from $r = 0$ to $r = R_{1}$ :
$Q_{1} = \int_{0}^{R_{1}} 4 π ρ_{0} r d r$
Calculating the integral:
$Q_{1} = 4 π ρ_{0} \int_{0}^{R_{1}} r d r = 4 π ρ_{0} {(\frac{r^{2}}{2})}_{0}^{R_{1}} = 4 π ρ_{0} \cdot \frac{R_{1}^{2}}{2} = 2 π ρ_{0} R_{1}^{2}$
Step 2: Calculate the charge of the hollow sphere
The hollow sphere has a surface charge density $σ$ and a radius $R_{2}$ . The total charge $Q_{2}$ on the hollow sphere is given by:
$Q_{2} = σ \cdot A = σ \cdot (4 π R_{2}^{2}) = 4 π R_{2}^{2} σ$
Step 3: Set the total charge to zero
According to the problem, the total charge in the system is zero:
$Q_{1} + Q_{2} = 0$
Substituting the expressions for $Q_{1}$ and $Q_{2}$ :
$2 π ρ_{0} R_{1}^{2} + 4 π R_{2}^{2} σ = 0$
Step 4: Rearranging the equation
Rearranging gives:
$4 π R_{2}^{2} σ = - 2 π ρ_{0} R_{1}^{2}$
Dividing both sides by $2 π$ :
$2 R_{2}^{2} σ = - ρ_{0} R_{1}^{2}$
Now, we can express $R_{2}^{2}$ in terms of $R_{1}^{2}$ :
$R_{2}^{2} = - \frac{ρ_{0} R_{1}^{2}}{2 σ}$
Step 5: Finding the ratio $\frac{R_{2}}{R_{1}}$
Taking the square root of both sides:
$R_{2} = R_{1} \sqrt{- \frac{ρ_{0}}{2 σ}}$
Thus, the ratio $\frac{R_{2}}{R_{1}}$ is:
$\frac{R_{2}}{R_{1}} = \sqrt{- \frac{ρ_{0}}{2 σ}}$
Final Answer
The ratio $\frac{R_{2}}{R_{1}}$ is:
$\frac{R_{2}}{R_{1}} = \sqrt{\frac{ρ_{0}}{2 σ}}$

Updated on:7/8/2024

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two charged spheres of radii $R_{1} and R_{2}$ having equal surface charge density. The ratio of their potential is
A $R_{1} / R_{2}$
B $R_{2} / R_{1}$
C ${(R_{1} / R_{2})}_{1}^{2}$
D ${(R_{2} / R_{1})}_{2}^{2}$
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density $ρ = \frac{A}{r}$ , where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
A $\frac{A R}{8 ε_{0}}$
B $\frac{A R}{4 ε_{0}}$
C $\frac{A R}{ε_{0}}$
D $\frac{A R}{2 ε_{0}}$
For the hemisphere of radius $R$ shown in the figure the surface charge density $σ$ varies with $θ$ (shown in figure) as $σ = σ_{0} cos θ$ the total charge on the sphere is

A $2 σ_{0} π R^{2}$
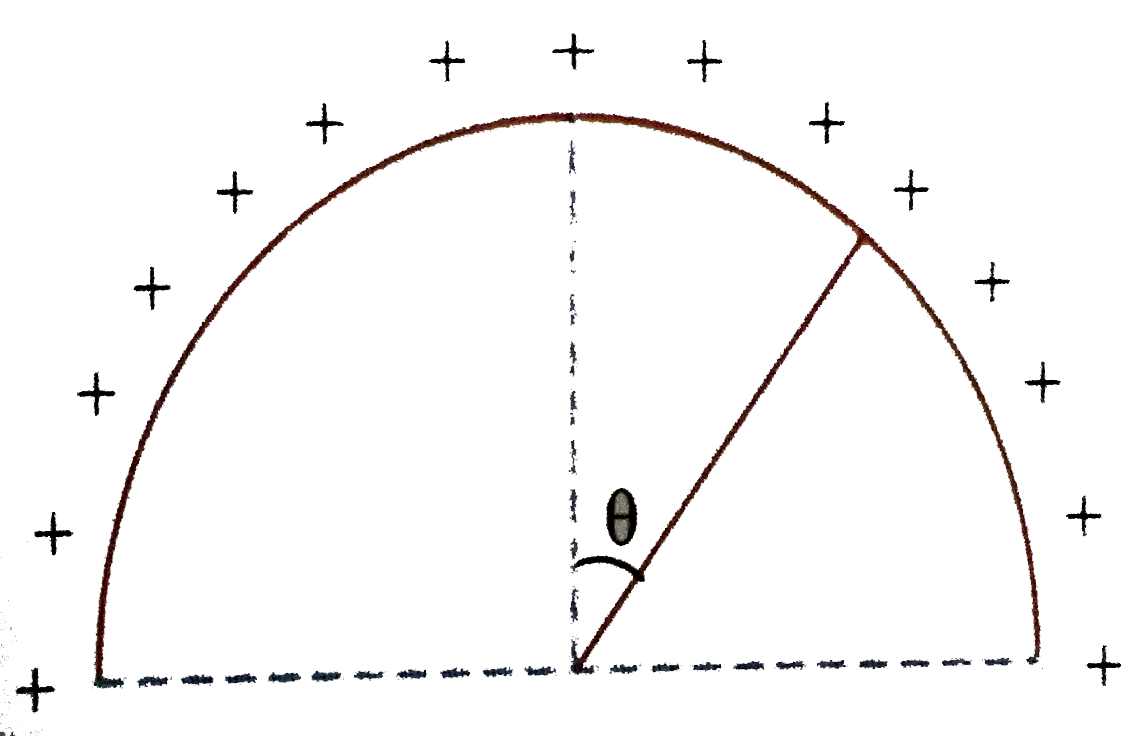B $\frac{σ_{0} π R^{2}}{2}$
C $\frac{σ_{0} π R^{2}}{3}$
D $σ_{0} π R^{2}$

CP SINGH-ELECTROSTATICS-Exercises

Home
Ask Doubt
Profile