For the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
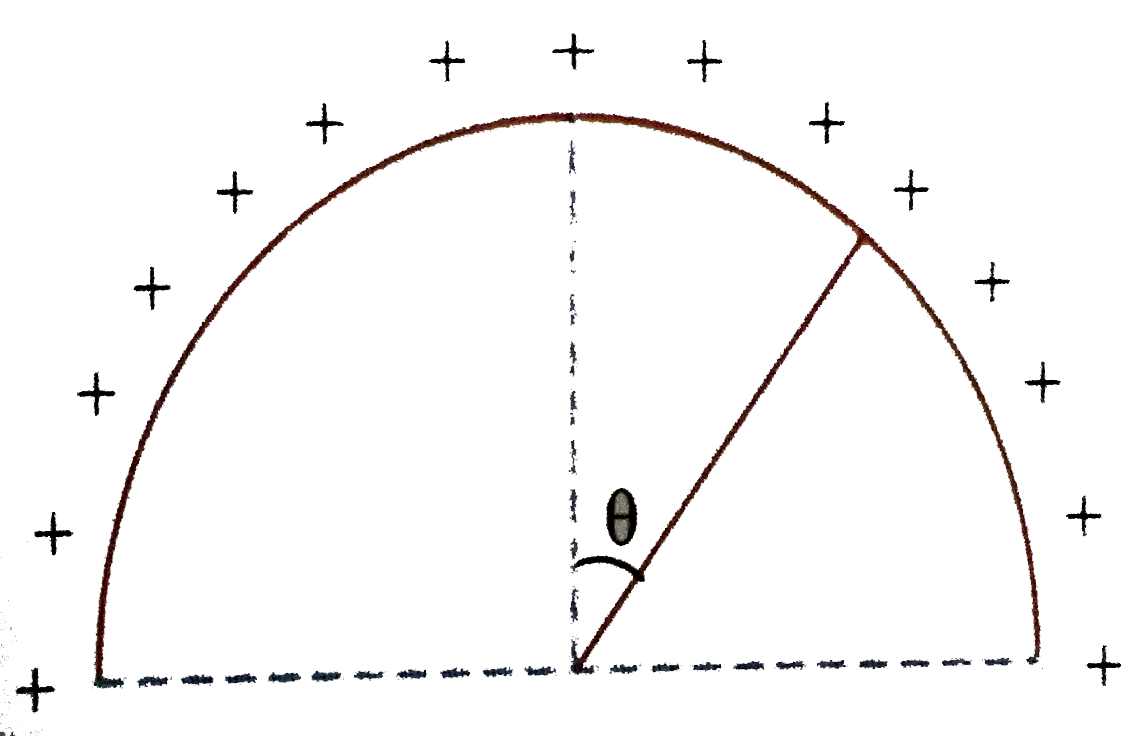
2σ0πR2
σ0πR22
σ0πR23
σ0πR2
The correct Answer is:D
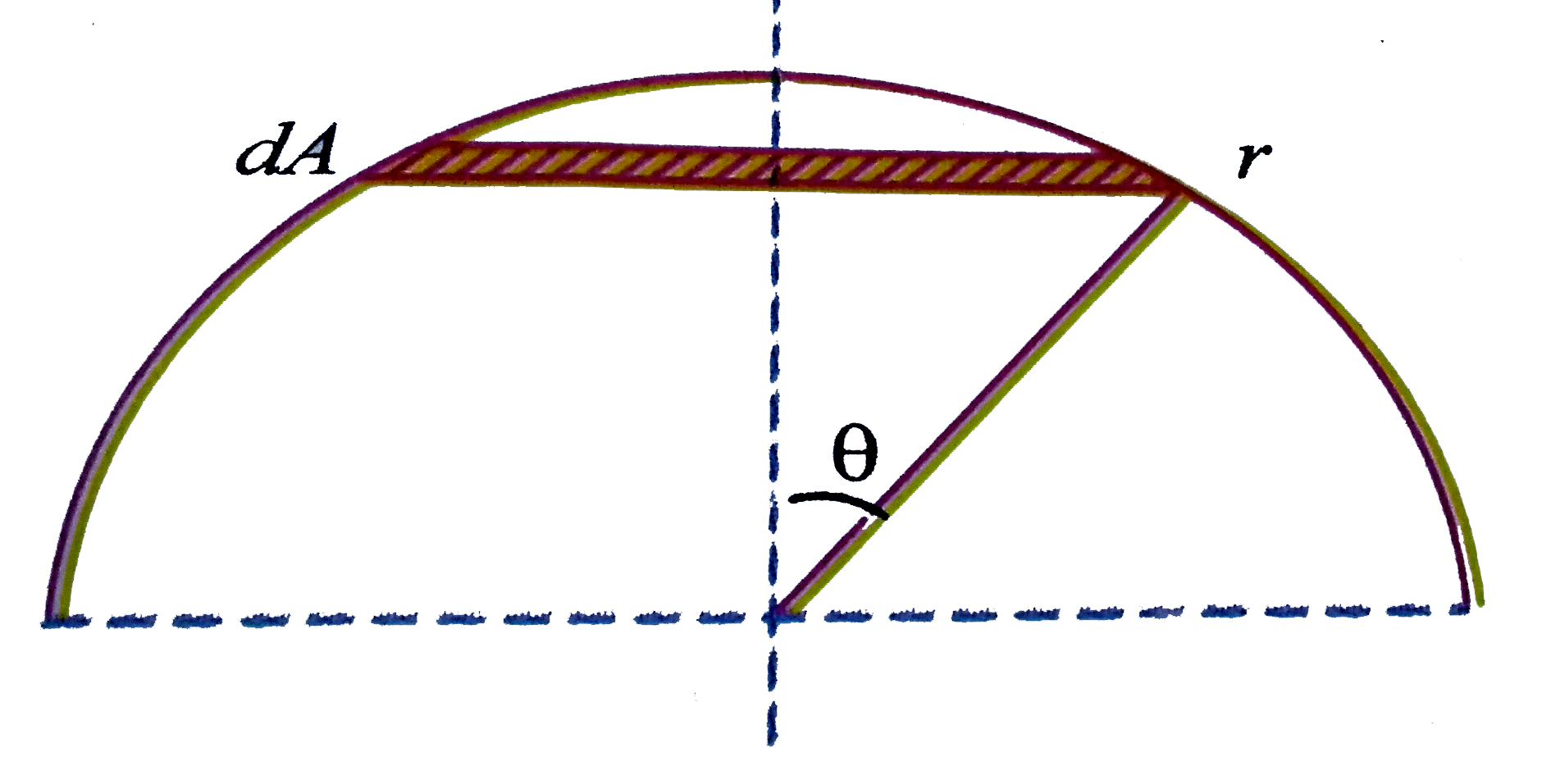
dA=2πrRdθ=2πR2sinθ(dθ)
dQ=2σ0πR2sinθcosθdθ=πσR2sin2θdθ
Q=πσ0R2∫π/20sin2θdθ=−πσ0R22(cos2θ)π/20
⇒q=πσ0R2
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage I
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage II
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Knowledge Check
The linear charge density of a uniform semicircular wire varies with θ shown in the figure as λ=λ0cosθ if R is the radius of the loop ,of the charge on the wire is
 Aλ0RB3λ0RC2λ0R3D2λ0R
Aλ0RB3λ0RC2λ0R3D2λ0RA sphere has surface charge density σ. It is surrounded by a spherical shell. The surface charge density on the spherical shell is
AσB−σCzeroDσ2The electric intensity at a point near a charged conductor of surface charge density σ is
AE=σ/∈0kBE=σ∈0kCE=σ/2∈0kDE=σ2
A solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be

View SolutionA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
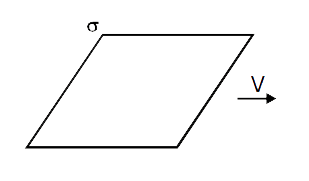
View SolutionA large plate with uniform surface charge density σ is moving with constant speed v as shown in the figure. The magnetic field at a small distance from plate is
View SolutionConductor of length l has shape of a semi cylinder of radius R(<<l). Cross section of the conductor is shown in the figure. Thickness of the conductor is (<<R) and conductivity of its material varies with angle θ according to the law σ=σ0cosθ where σ0 is a constant. If a battery of emf ε is connected across its end faces (across the semi-circular cross-sections), the magnetic induction at the mid point O of the axis of the semi-cylinder is :

View SolutionThere are three concentric thin spheres of radius a,b,c(a>b>c). The total surface charge densities on their surfaces are σ,−σ,σ respectively. The magnitude of the electric field at r (distance from centre) such that a>r>b is:
View Solution

