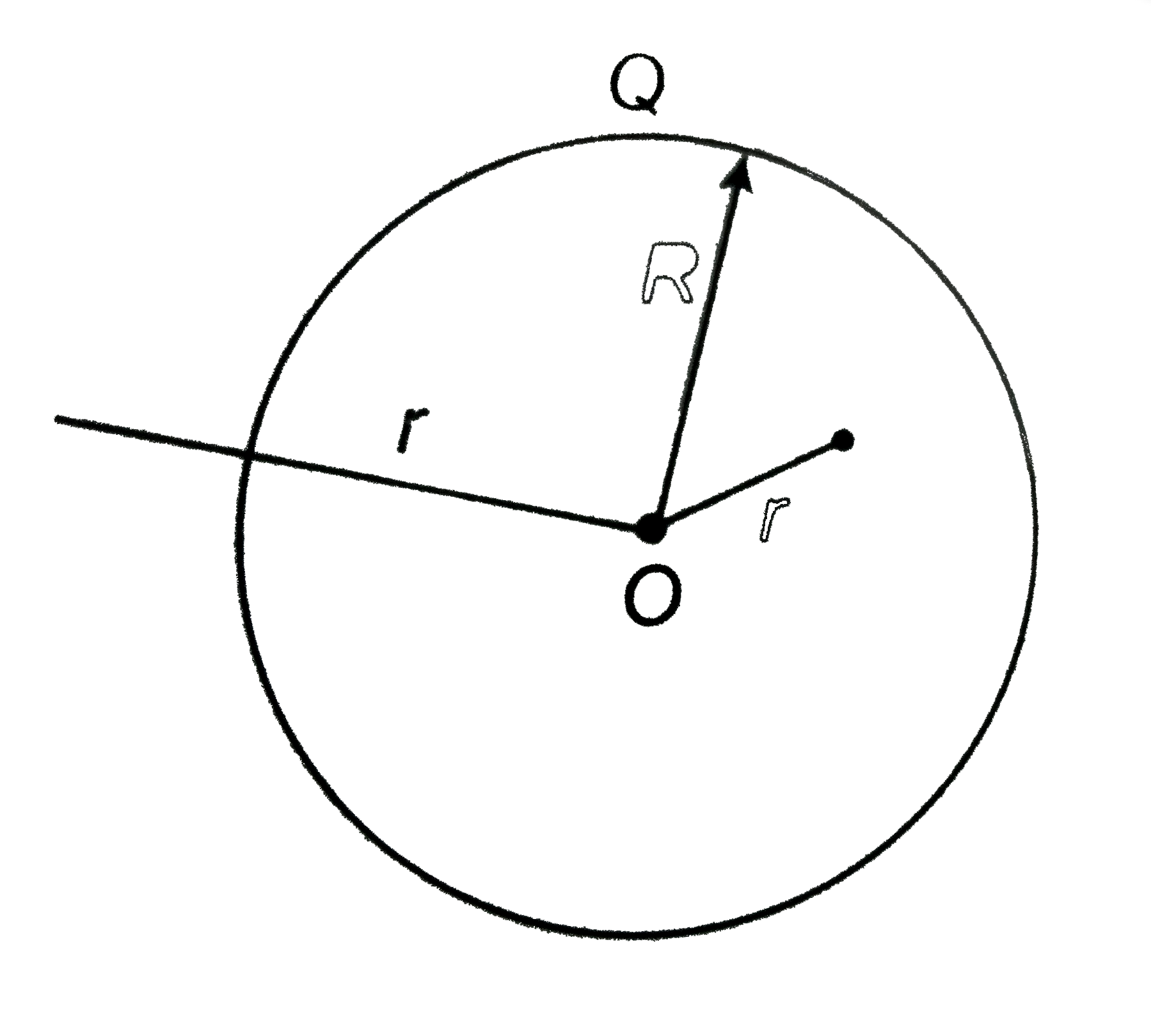
A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
The electric potential energy is equal to work done in bringing charges from infinity and place them on the shell .
Let at some instant , a charge q be placed on the shell. The potential at the surface is
V=14π∈0.qR
The work done in bringing a charge dq from infinity to this shell.
dW=(dq)V=qdq4π∈0R
Total work done
W=∫Q0qdq4π∈0R=14π∈0R∣∣∣q22∣∣∣Q0
=U=Q28π∈0R
Alternative method : The energy stored per unit in electric field i.e. energy density
u=12∈0E2
Inside shell (r<R),E=0
Outside shell (r>R),E=14π∈0.Qr2
The energy density outside shell : u=12∈0E2
Take a small volume (a spherical shell of radius r and thickness dr)
dV=4πr2dr
Small energy stored in this volume
dU=udV=12∈0E2.4πr2dr
=12∈0(14π∈0Qr2)2.4πr2dr
U=Q28π∈0∫∞Rdrr2=Q28π∈0R
Topper's Solved these Questions
Similar Questions
Find the electric potential energy of a uniformly charged sphere.
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View Solution
Knowledge Check
A charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
A0B−Q4πε0RCQ4πε0(2R)D2Q4πε0RA charge Q is uniformly distributed only on the fourths portion of a ring of radius R. The elctric potential at centre of ring is
A3Q4πε0RBQ4πε0RC3Q2πε0RD6Q4πε0RA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?
 A
A B
B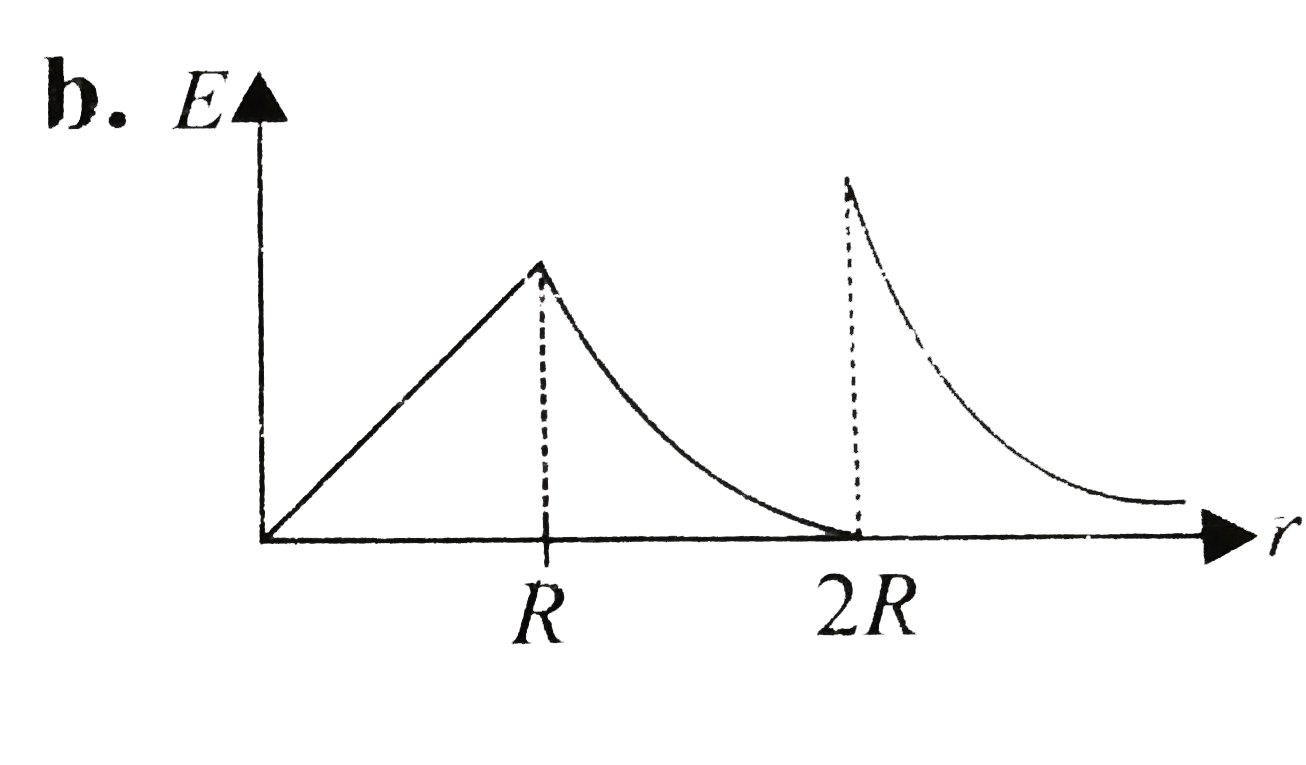 C
C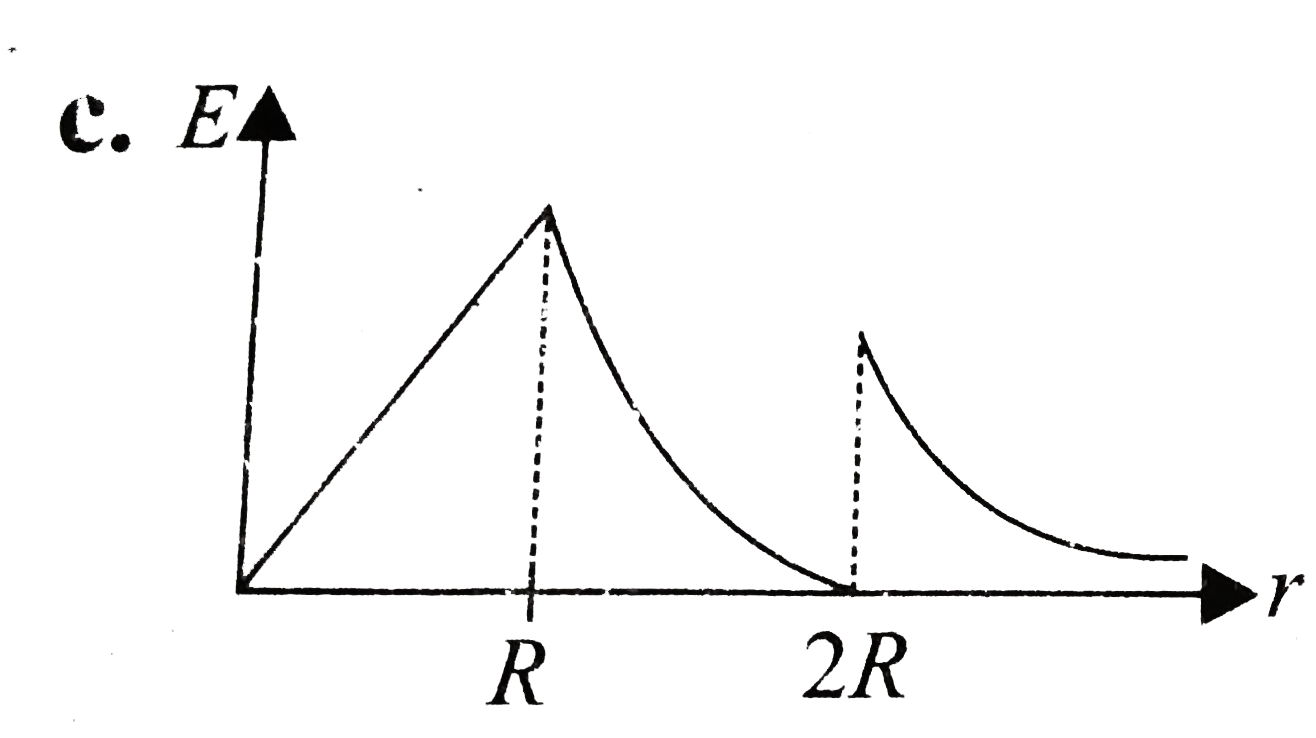 D
D
There is a hemispherical shell having charge Q uniformly distributed on its surface. Radius of the shell is R. Find electric potential and field at the centre (of the sphere).
View SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionA charge Q is distribution over a metal sphere of radius R. What is the electric field and electric potential at the centre ?
View SolutionThe electric potential inside a conducting sphere
View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View Solution
