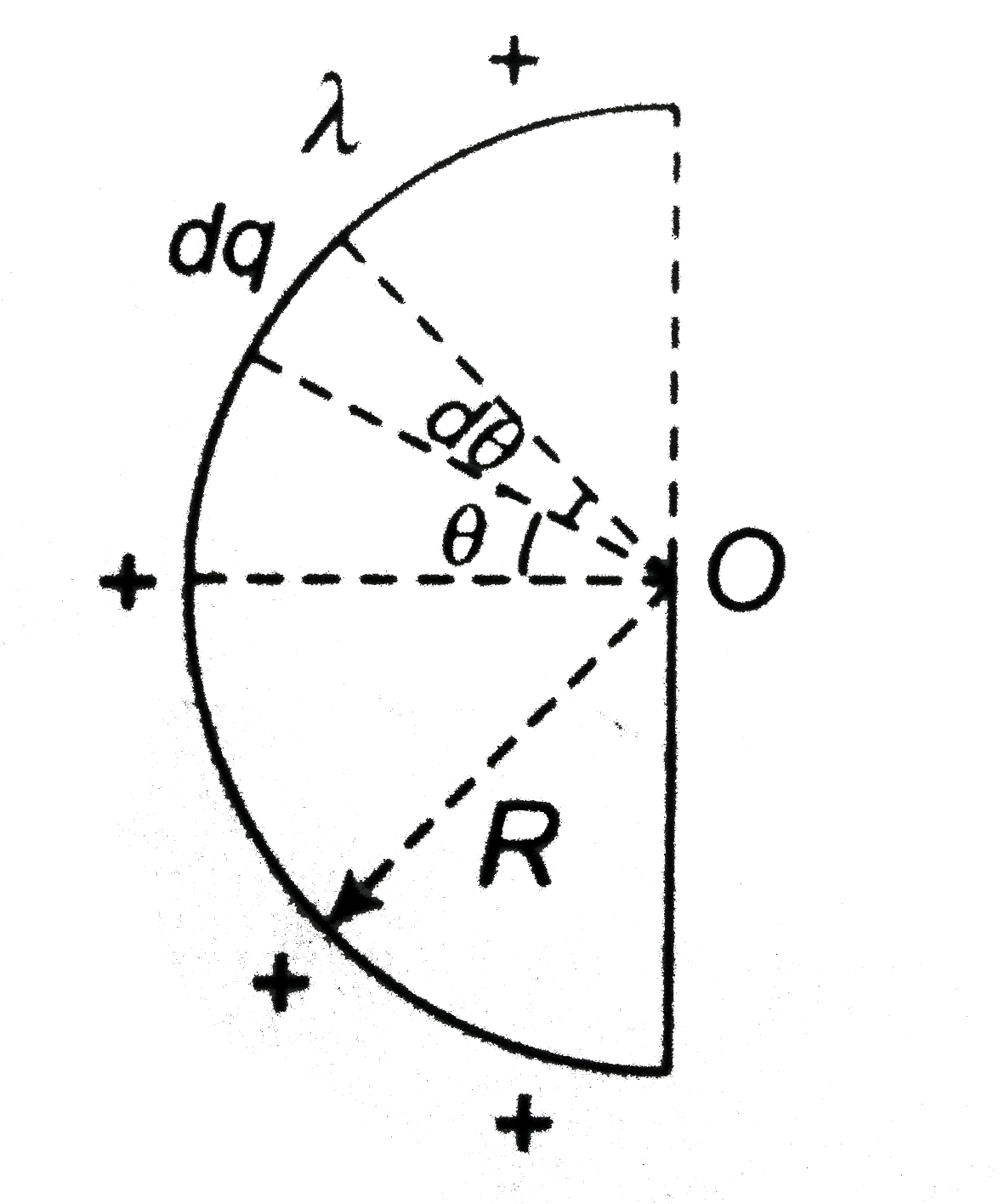
A quarter ring of radius $R$ is having uniform charge density $λ$ . Find the electric field and potential at the centre of the ring.

Video Solution

Text Solution

Verified by Experts

To take element on circular length , take a small length of angle $d θ$ at angle $θ$ as shown.
$d l = R d θ$
$d q = λ d l = λ R d θ$
$d E_{0} = \frac{1}{4 π \in_{0}} . \frac{d q}{R^{2}} = \frac{λ d θ}{4 π \in_{0} R}$
This expression cannot be integrated because direction of electric field at $O$ is different for various small $d q$ .The components of $d E_{0}$ along $x$ - and $y$ -axis can be integrated.
$E_{x} = \int d E_{x} = \int d E cos θ = \frac{λ}{4 π \in_{0} R} \int_{- π / 2}^{π / 2} cos θ d θ$
$\int_{- π / 2}^{π / 2} cos θ d θ = {| sin θ |}_{- π / 2}^{π / 2} = sin (π / 2) - sin (- π / 2)$
$= 1 - (- 1) = 2$
$E_{x} = \frac{λ}{2 π \in_{0} R}$
$E_{y} = \int d E_{y} = \int d E sin θ = \frac{λ}{4 π \in_{0} R} \int_{- π / 2}^{π / 2} sin θ d θ$
$\int_{- π / 2}^{π / 2} sin θ d θ = {| - cos θ |}_{- π / 2}^{π / 2} = 0$
$E_{y} = 0$ or we can say by symmetry , $E_{y} = 0$
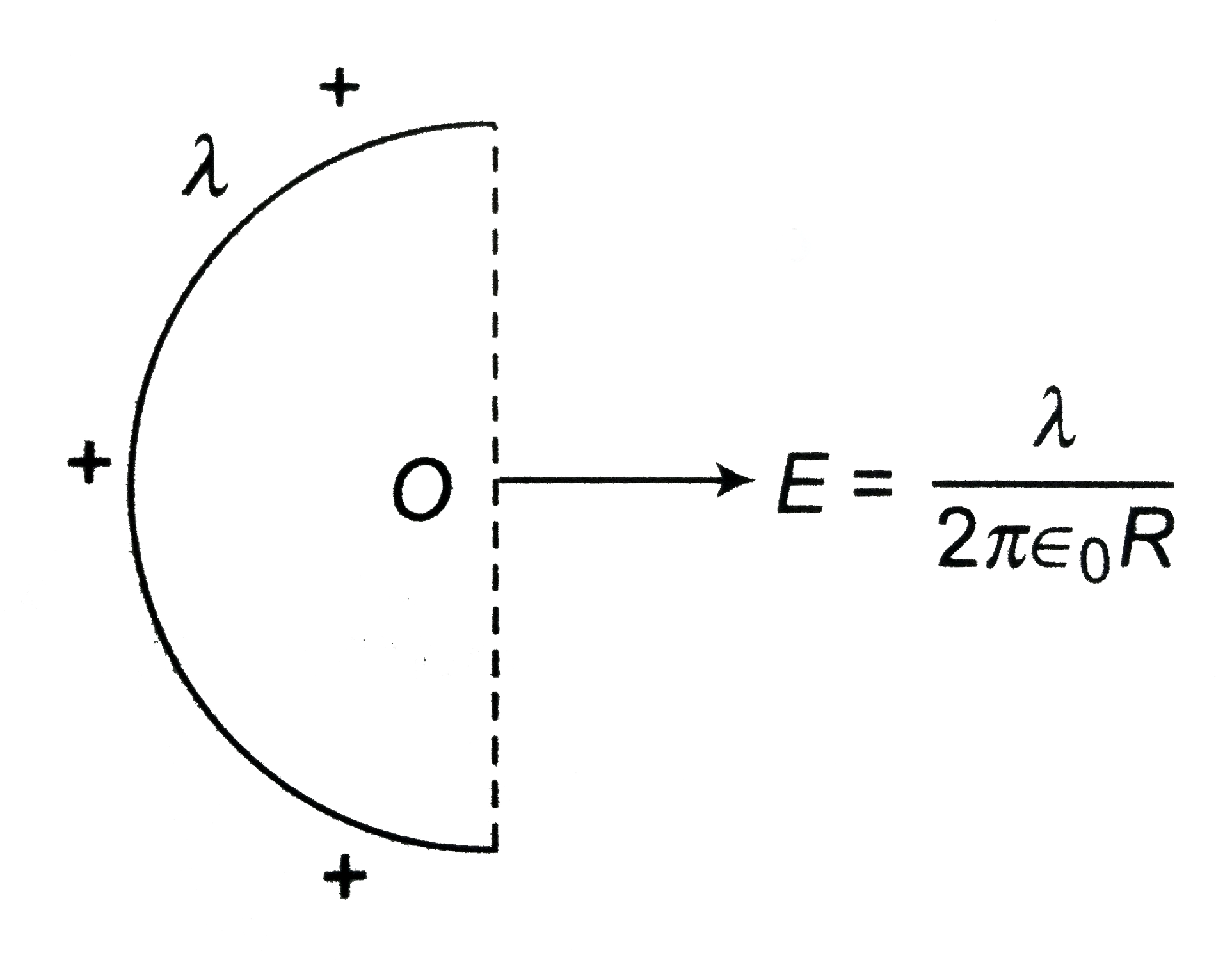
Electric field at $O$
$E_{0} = E_{x} = \frac{λ}{4 π \in_{0} R}$
$V_{0} = \frac{1}{4 π \in_{0}} . \frac{λ . π R}{R} = \frac{λ}{2 \in_{0}}$

Updated on:21/07/2023

A half ring of radius $r$ has a linear charge density $λ$ .The potential at the centre of the half ring is
A $\frac{λ}{4 ε o {ln}_{0}}$
B $\frac{λ}{4 π^{2} ε_{0} r}$
C $\frac{λ}{4 π ε_{0} r}$
D $\frac{λ}{4 π ε_{0} r^{2}}$
The electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be $Q$ and its radius be $R$ ?
A $\frac{1}{4 π ε_{0}} \frac{Q}{π R^{2}}, \frac{1}{4 π ε_{0}} \frac{Q}{π R}$
B $\frac{1}{4 π ε_{0}} \frac{Q}{R^{2}}, \frac{1}{4 π ε_{0}} \frac{2 Q}{π R}$
C $\frac{1}{4 π ε_{0}} \frac{2 Q}{π R^{2}}, \frac{1}{4 π ε_{0}} \frac{Q}{R}$
D $\frac{1}{4 π ε_{0}} \frac{2 Q}{R^{2}}, \frac{1}{4 π ε_{0}} \frac{3 Q}{π R}$
An insulated sphere of radius $r$ haas a uniform volume charge density $λ$ . The electric field at a point $A$ , which is at distance $r$ from its centre is given by $(R > r)$
AZero
B $R λ / 3 \in_{0}$
C $\frac{2 r λ}{3 \in_{0}}$
D $\frac{r λ}{3 \in_{0}}$