A charged particle (q,m) is released from origin in an electric field E=α−βx where α and β are constants and x is distance from origin. Find the velocity of particle in terms of x and maximum displacement of the particle.
When the particle is at distance x from origin , the force on it is F=qE.
Acceleration of a particle , a=qEm=q(α−βx)m
Here , acceleration a is a variable .
vdvdx=q(α−βx)m
∫v0vdx=qm∫x0(α−βx)dx
∣∣∣v22∣∣∣v0=qm∣∣∣αx−βx22∣∣∣x0
v22=qm(αx−βx22)
v=√qm(2αx−βx2)
when particle stops , v=0 .
x=x0=2αβ
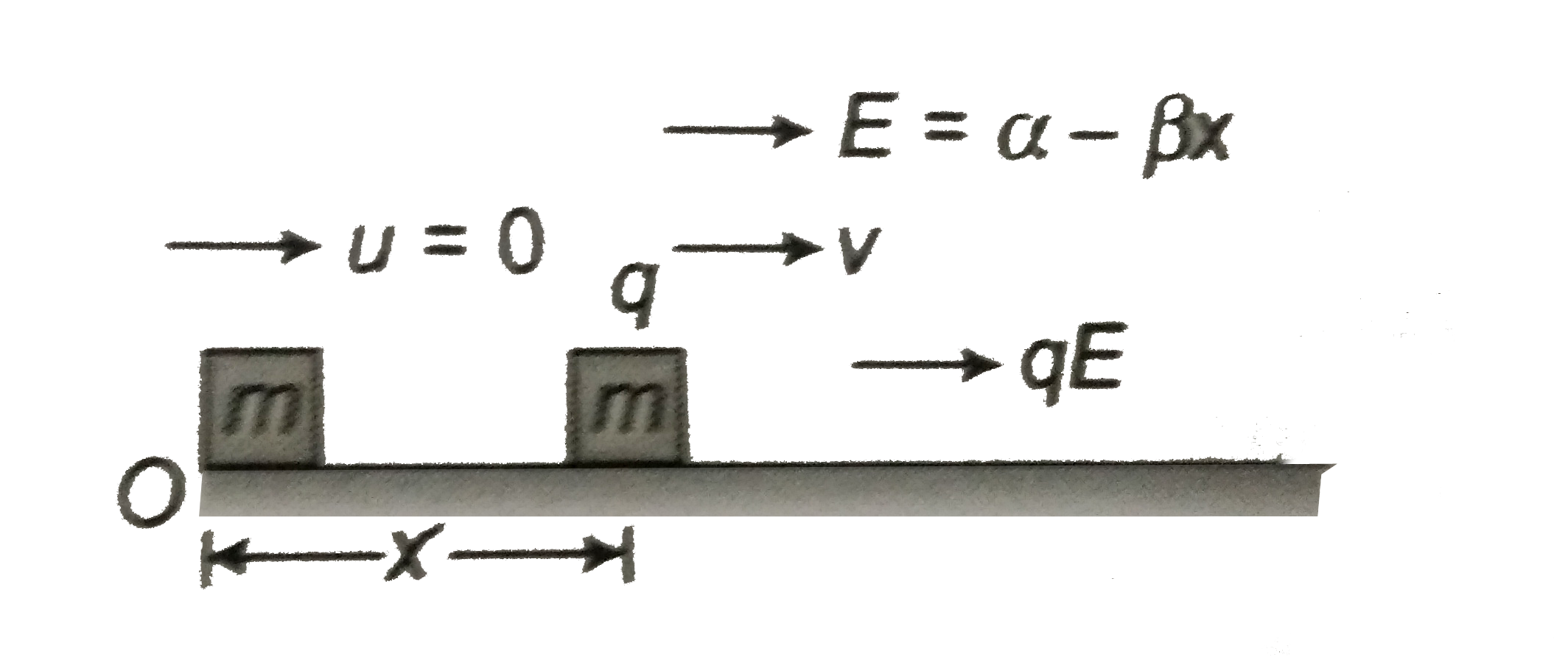
Topper's Solved these Questions
Similar Questions
A particle starts from rest with acceleration a=αt+βt2 where α and β are constants. Find its displacement between t = 1 and t= 2 second.
View SolutionA particle with specific charge q/m moves rectilinerarly due to an electric field E=E0−ax, where a is a positive constant, x is the distance from the point where the particle was initially at rest. Find:
(a) the distance covered by the particle till the moment it came to a standstill,
(b) the acceleration of the particle at that moment.
View Solution
Knowledge Check
A particle of charge q and mass m moves rectilinearly under the action of an electric field E=α−βx. Here, α and β are positive constants and x is the distance from the point where the particle was initially at rest. Then, the
Amotion of the particle is oscillatoryBamplitude of the particle is (α/β)Cmean position of the particle is at x=(α/β)Dmaximum acceleration of the particle is qαm.The relation between time t and displacement x is t=αx2+βx, where αandβ are constants. The retardation is
A2αv3B2βv3C2αβv3D2β2v3Energy due to position of a particle is given by, U=α√yy+β, where α and β are constants, y is distance. The dimensions of (α×β) are
A[M0LT0]B[M1/2L3/2T−2]C[M0L−7/2T0]D[ML7/2T−2]
A particle of charge q and mass m moves rectilinearly under the action of an electric field E=A−Bx, where B is a positive constant and x is a distance from the point where the particle was initially at rest. The distance travelled by the particle till it comes to rest is αAβB. Find (α+β).
View SolutionThe instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
View SolutionA particle is acted upon by a force given by F=−αx3−βx4 where α and β are positive constants. At the point x = 0, the particle is –
View SolutionThe displacement x of a particle varies with time as x=aeαt+beβt where a,b,a, β are constants and are positives. The velocity of the particle will:
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View Solution