A particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
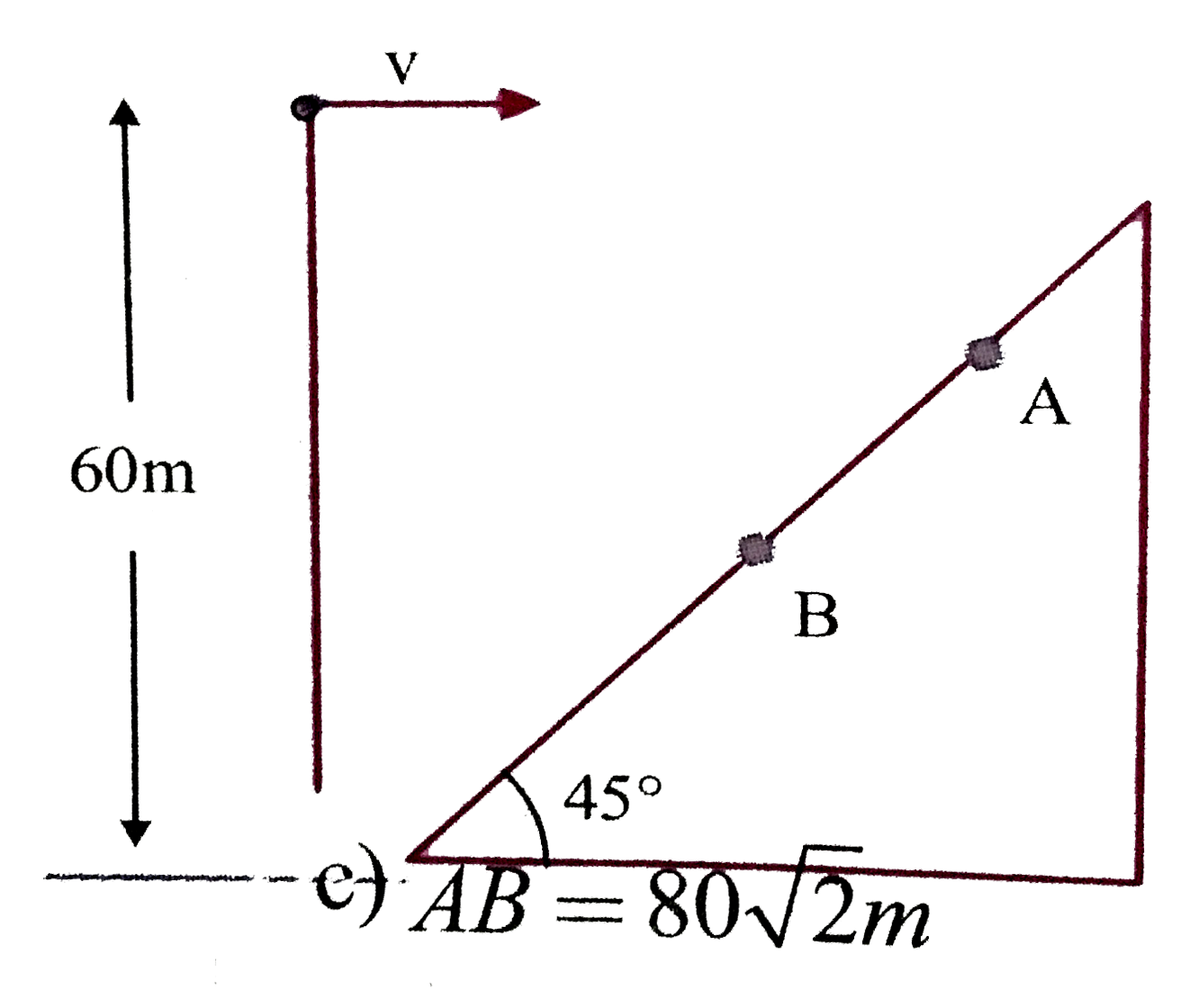
v=20m/s
v=10m/s
AB=80√2m
AB=80m
The correct Answer is:A, C

u1x=vcos450,a1x=−gsin450u1y=−vsin450,a1y=−gcos450
At point
v1x=0⇒0=vcos450−gsin450t,t=v/g
Tan450=h−12gt2vt, h−12gt2=vt
h=12g[v2g2]+v2g
h=v2g+v22g=3v22g, v=√2gh3=20m/s
v'= velocity just before collision =√2
v''= velocity after collision =v
tAB=2vgcos450=2√2vg=4√2sec
AB=12×10×1√2×16×2=80√2m
Topper's Solved these Questions
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Comprehension type
Explore 35 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Subjective type Questions
Explore 9 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:INTEGER TYPE QUESTIONS
Explore 8 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL II(H.W)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution
Knowledge Check
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

What is the velocity of the particle just before it hits the plane?A5√3m/sB52√13m/sC10√13m/sD5√26m/sA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
A2v2gB√2[2v2g]Cv2gD√2v2gA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
Find the time taken by the particle to hit the plane.A34sB3sC4sD43s
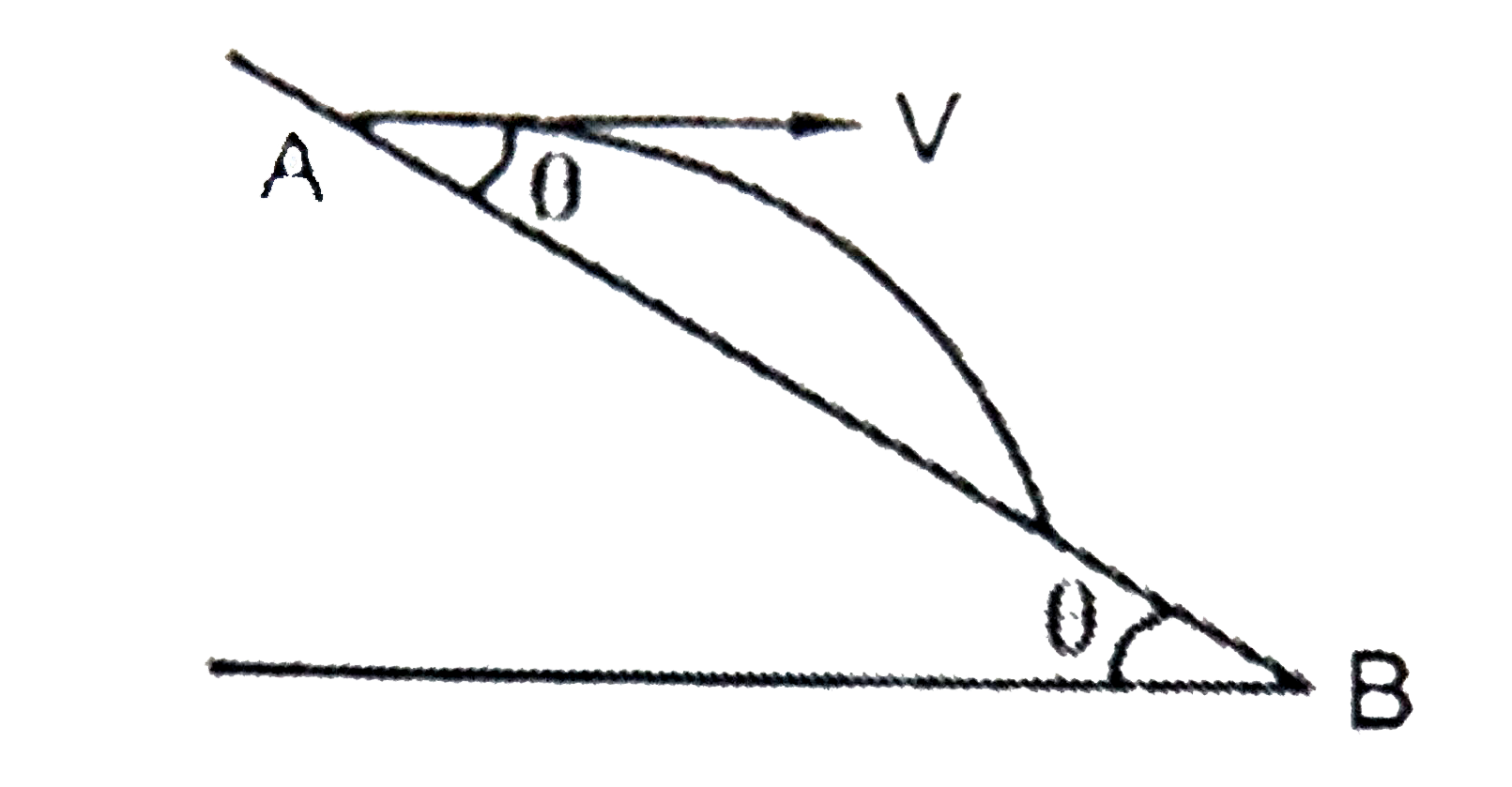
A particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

How far from the point of projection will the particle strike the plane?
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View Solution

