A simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being 2√5
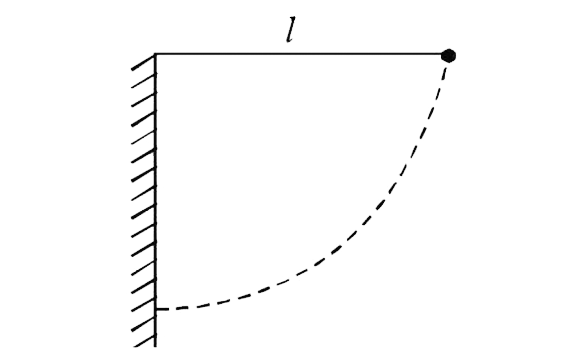
what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
The correct Answer is:4
When simple pendulum released from position A strikes the wall with velocity v then by conservation of mechanical energy.
mgL+0=12mv2+0,i.e.v=√2gL
Now as coefficient of restitution is e so, speed of pendulum after first collision will be v1=ev=e√2gL
Now after completing Oscillation in accordance with conservation of mechanical energy it will strike the wall with same velocity and so its velocity after second collision will be
v2=ev1=e(e√2gL)=e2√2gL
So the velocity of the pendulum after n collision will be vn=env=en√2gL
Now if it rises to a height h, by conservation of mechanical energy
12m(Vn)2=mgh,i.e.,e2n2gL=gh

e2n=hL=L(1−cosθ)L
or
(2√5)2n=1−cosθ[ase=2√2]or(45)n=1−cosθ
Now for θ to be lesser than 60,cosθ>(1/2)
i.e., 1−cosθ<12
So, (45)n<12or(54)n>2 or
n(log10−3log2)>log2
or n>0.3010.097[aslog10=1andlog2=0.3]
or >3.1
As n (no.of collisions) must be integer so for θ<60∘,n=4.
Topper's Solved these Questions
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Multiple Answer
11 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Comprehension type
35 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)
54 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
Similar Questions
Two point masses are connected by a light intextensible string are lying on a frictionless surface as shown in figure. An impulse of magnitude 10kg−m/s is given to 5kg block.
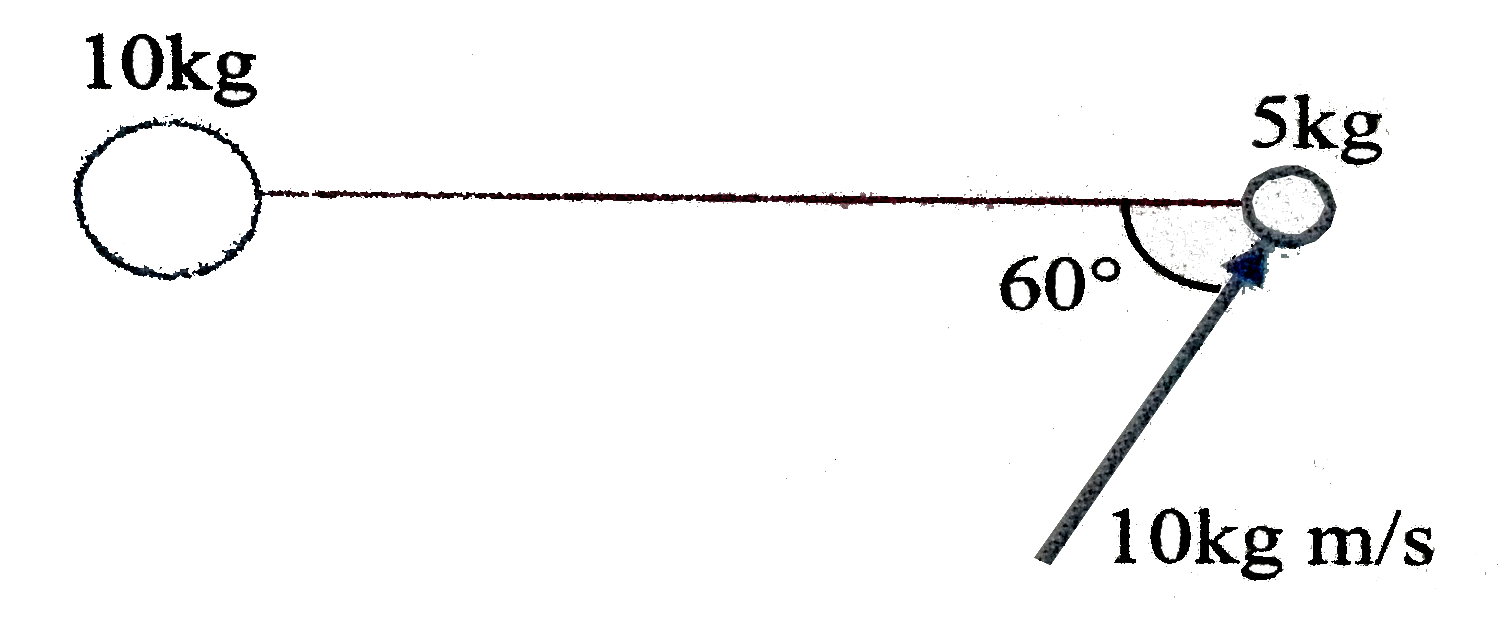
View SolutionA small ball is projected at an angle α between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View SolutionA bicycle chain of length 1.6m and of mass 1kg is lying on a horizontal floor. If g=10ms−2, the work done in lifting it with one end touching the floor and the other end 1.6m above the floor is
View SolutionA ball of mass 0.2 kg is thrown vertically upwards by applying a force by hand. If the hand moves 0.2 m while applying the force and the ball goes upto 2 m height further, find the magnitude of the force. (Consider g=10m/s2).
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O.
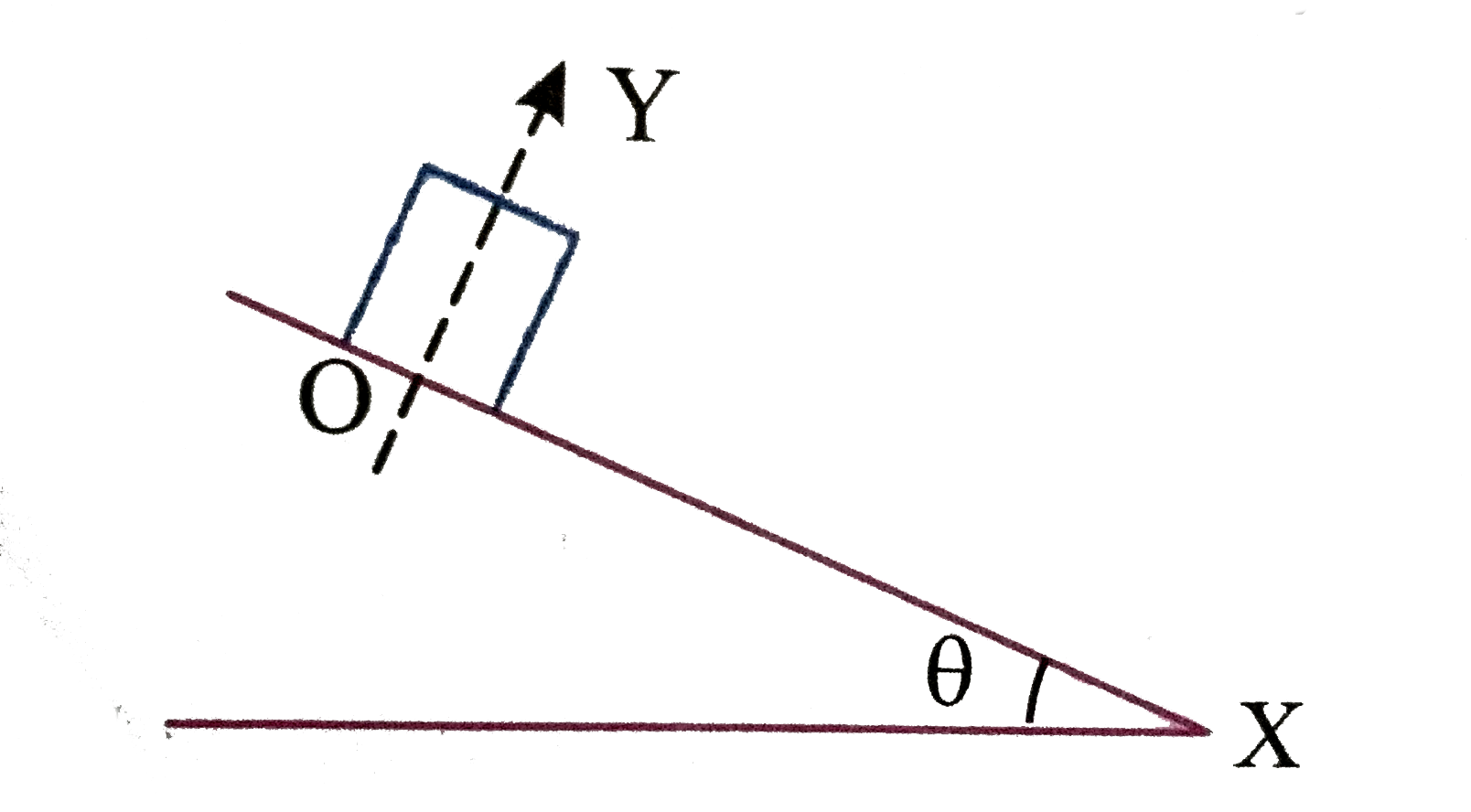
The maximum velocity of block will be:
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being (2)/(sqrt(5) what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is (2)/(sqrt(5)) . After how many collisions the amplitude of vibration will becomes less then 60^(@) .
View SolutionA simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30^(@) with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e = (2)/(sqrt(5)) Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30^(@)
View SolutionA simple pendulum is hanging from a peg inserted in a vertical wall. Its bob is stretched in horizontal position from the wall and is left free to move. The bob hits on the wall the coefficient of restitution After how many collsions the amplitude of vibration will become less than 60∘
View SolutionThe figure shows a pendulum of length l suspended at a distance x vertically above a peg. (a) The pendulum bob is deflected through an angle theta and then released. Find the speed of the bob at the instant (b) The pendulum is released when theta = 90^(@) . For what x (position of peg) will the pendulum complete the circle ? (c) The pendulum is released when theta = 60^(@) . what is the velocity of the bob as it passes position E.
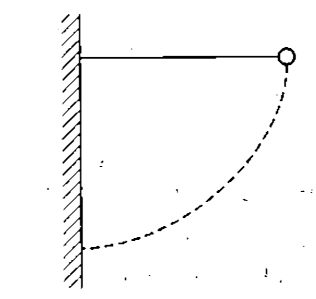
View SolutionA simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
View SolutionA pendulum bob on a 2 m string is displaced 60^(@) from the verticle and then released . What is the speed of the bob as it passes through the lowest point in its path?
View SolutionA ladder 5 m long is leaning against a well. The bottom of the ladder is pulled along the ground, away from the well, at the rate of 2 m/s. How fat is its height on the wall decreasing when the foot of the ladder is 4m away from the wall?
View Solutionएक सरल लोलक खूँटी (Peg) की सहायता से ऊर्ध्वाघर दीवार पर लटकाया गंया है। लोलक को खींचकर चित्रानुसार दीवार से दूर क्षैतिज स्थिति में लाया जाता है तथा छोड़ दिया जाता है। गोलक दीवार से टकराता है, यदि प्रत्यावस्थान गुणांक (Coefficient of restitution) 2√5, हो, तो संघट्टों की कम-से-कम कितनी संख्या होगी, जिनके बाद दोलनों का आयाम 60∘ से कम रह जाएगा?
View SolutionFrom a rod fixed on a vertical wall, a simple pendulum is suspended. Its bob is pulled away from the wall to a horizontal position and then released. If the coefficient of restitution is 2/sqrt(5) , what would be the minimum number of impacts of the bob with the wall, after which the amplitude of the pendulum becomes less than 60^@ ?
View SolutionA second pendulum is shifted 4 cm away from its equilibrium position and then released. After 2s the pendulum is 3 cm away from its position of equilibrium. What will be the position of the pendulum after another 2 s?
View Solution