A small ball of mass 'm' is connected by an intextensible mass less string of length ('l'=10m) with an another ball of mass M=4m. They are released with zero tension in the string from a height h(h=5m) as shown. Find the time when the string becomes taut for the first time after the mass 'M' collides with the ground is _____S. (Take all collisions to be elastic) (g=10m/s2)

The correct Answer is:1
Just after collision velocities of both the balls will be √2gh in opposite direction. Relative acceleration between the two ball is zero and relative velocity of approach is 2√2gh.
Hence they will collide after a time t=l2√2gh At the time of collision of two balls relative velocity of approach = relative velocity of separate =2√2gh
Hence string becomes tigt after the same time
t=l2√2gh
Hence the total time will be (2t)=l2√2gh=1s

Topper's Solved these Questions
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Multiple Answer
11 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Comprehension type
35 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)
54 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
Similar Questions
A small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M=4m. They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.

View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View Solution
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
A0B0.4C0.8D1.2The linear mass density 'μ' of the string is (where, mass of the string = m, length of the string = L)
AmLBmLCmt2DmL3
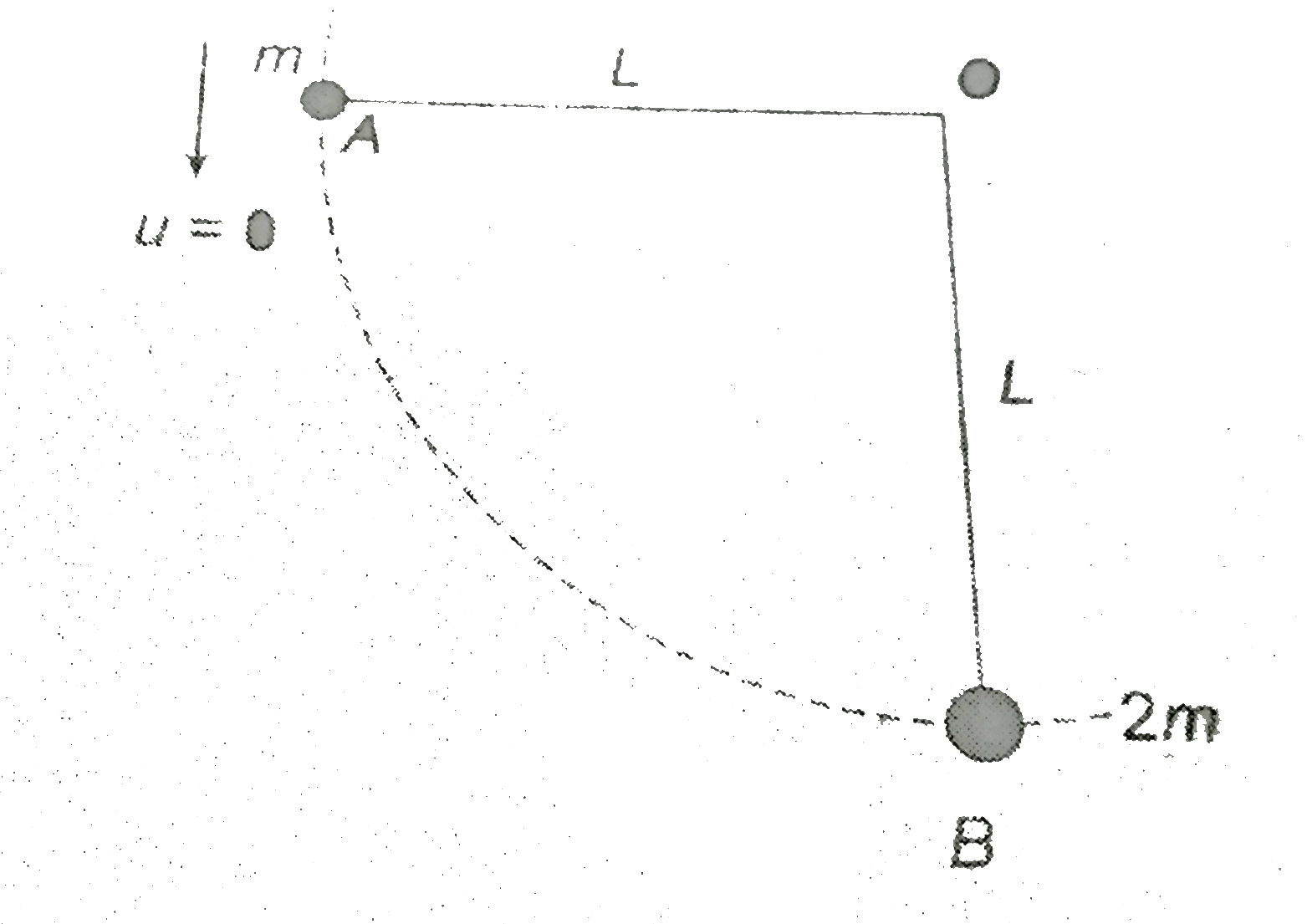
A ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

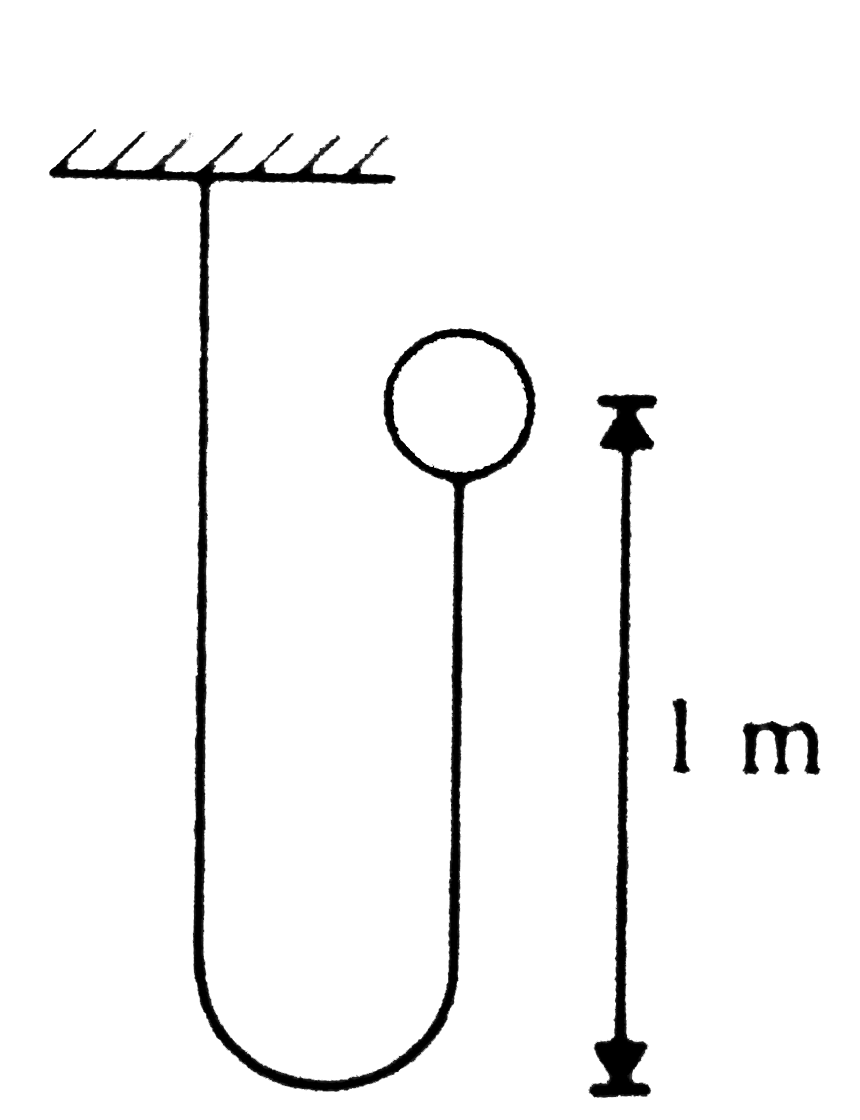
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
View SolutionThe block shown in figure has a mass M and descends with an acceleration a. the mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

View SolutionThe linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
View Solution