A simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30∘ with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e=2√5
Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30∘

The correct Answer is:4
Step by step video, text & image solution for A simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30^(@) with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e = (2)/(sqrt(5)) Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30^(@) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy
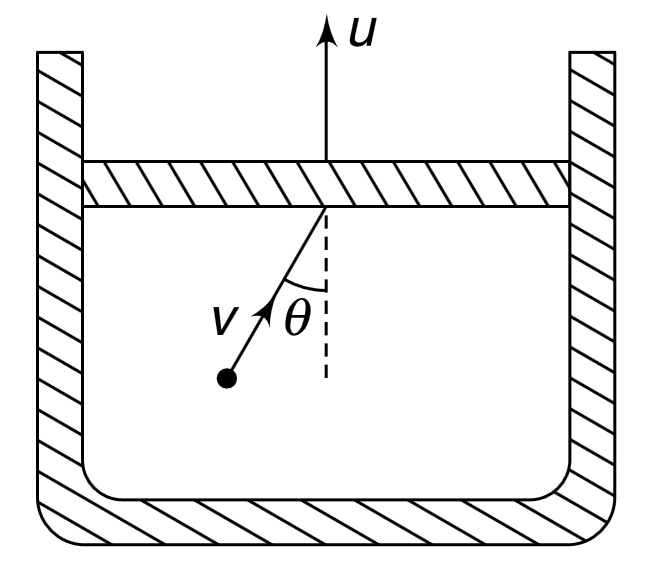
View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being (2)/(sqrt(5) what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is (2)/(sqrt(5)) . After how many collisions the amplitude of vibration will becomes less then 60^(@) .
View SolutionA pendulum of length 1 m hangs from an inclined wall. Suppose that this pendulum is released at an initial angle of 10^(@) and it bounces off the wall elastically when it reaches an angle of -5^(@) as shown in the figure. Take g = pi^(2) m//s^(2) . The period of this pendulum is (in second)
View SolutionA simple pendulum is hanging from a peg inserted in a vertical wall. Its bob is stretched in horizontal position from the wall and is left free to move. The bob hits on the wall the coefficient of restitution After how many collsions the amplitude of vibration will become less than 60∘
View SolutionThe string of a simple pendulum can with stand a maximum tension equal to 4 times the weight of bob suspended to it. The string is made horizontal and bob is released from rest then:
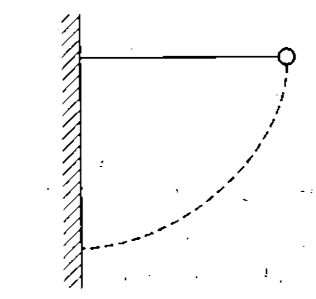
View SolutionA simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
View Solutionएक सरल लोलक खूँटी (Peg) की सहायता से ऊर्ध्वाघर दीवार पर लटकाया गंया है। लोलक को खींचकर चित्रानुसार दीवार से दूर क्षैतिज स्थिति में लाया जाता है तथा छोड़ दिया जाता है। गोलक दीवार से टकराता है, यदि प्रत्यावस्थान गुणांक (Coefficient of restitution) 2√5, हो, तो संघट्टों की कम-से-कम कितनी संख्या होगी, जिनके बाद दोलनों का आयाम 60∘ से कम रह जाएगा?
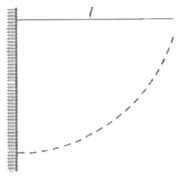
View SolutionFrom a rod fixed on a vertical wall, a simple pendulum is suspended. Its bob is pulled away from the wall to a horizontal position and then released. If the coefficient of restitution is 2/sqrt(5) , what would be the minimum number of impacts of the bob with the wall, after which the amplitude of the pendulum becomes less than 60^@ ?
View SolutionEffective length of a simple pendulum is 50 cm and mass of the bob suspended is 4 g. The bob is pulled to one side to make the string horizontal and then it is released. What will be the kinetic energy of the bob when it makes an angle 60^(@) with the vertical?
View SolutionA simple pendulum ia hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is 2√5. After how many collision the amplitude of vibration will become less than 60∘ (Hint : hn≤h(1−cosθ))
View SolutionA simple pendulum is hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is 2√5 After how many collision the amplitude of vibration will become less than 60° (Hint: hn≤h(1−cosθ))
View SolutionA simple pendulum is hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is 2√5. After how many collisions the amplitude of vibration will become less than 60∘
View SolutionA simple pendulum is hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is (2)/(sqrt(5)) . After how many collisions the amplitude of vibration will become less than 60^(@)
View Solution
