A block of mass M is placed on a smooth table. Its two sides are attached to the fixed walls by means of collinear horizontal springs of spring constants K1 and K2 respectively (K1>K2) as shown in the figure. The block is made to oscillate horizontally along the line of two springs. The frequency of its oscillation is
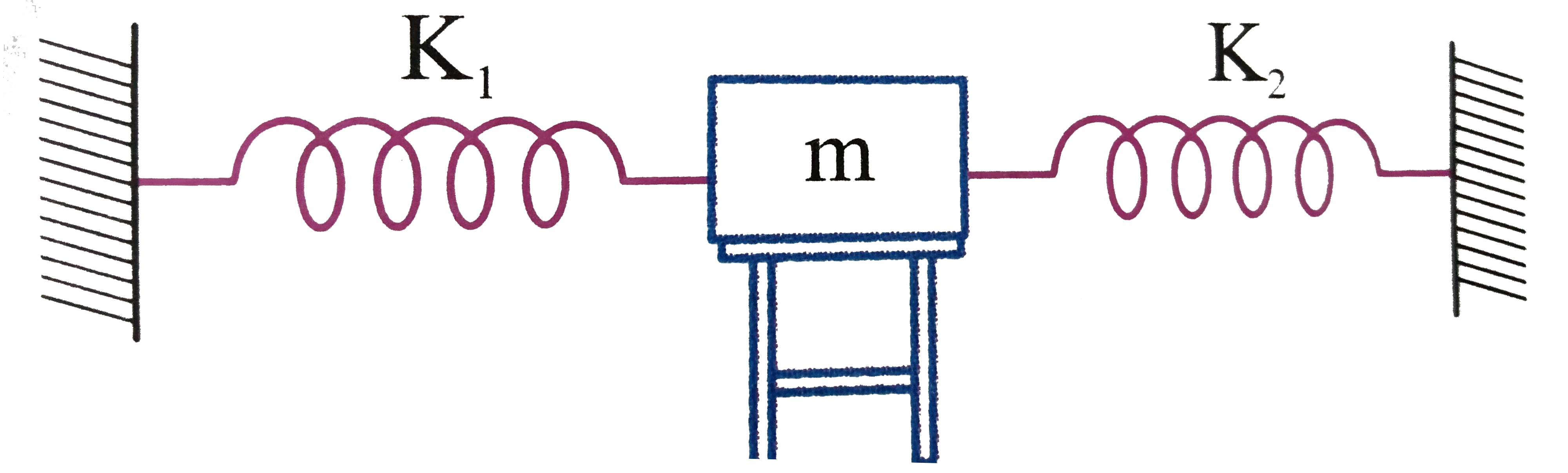
12π ⎷(K1K2(K1+K2)M)
12π√(MK1+K2)
12π√(K1+K2M)
12π√(K1−K2M)
The correct Answer is:C
The springs are parallel
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:SIMPLE PENDULUM
Explore 14 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:DAMPED AND FORCED OSCILLATIONS
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:ENERGY OF A PARTICLE EXECUTING SHM
Explore 9 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View SolutionTwo springs of force constants K1 and K2 are connected to a mass m as shown I the figure.

If both K1 and K2 are made four times their original values, the frequency of oscillation becomes,
View Solution
Knowledge Check
A mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is
 AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mgA uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 A12π√2kMB12π√kMC12π√6kMD12π√24kM
A12π√2kMB12π√kMC12π√6kMD12π√24kMTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
A block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo particles A and B of equal masses are suspended from two massless springs of spring constants K1andK2 respectively. If the maximum velocities during oscillations are equal. the ratio of the amplitude of A and B is
View SolutionA simple harmonic motion oscillator has two springs of spring constant k and other two of spring constant 2k, arranged as shown in the figure. Calculate the time period of oscillator.
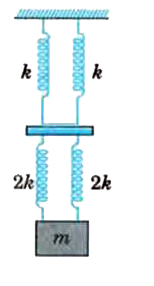
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View Solution
