A light sprial spring supports 200g weight at its lower end oscillates with a period of 1s. The weight that must be removed from the lower end to reduce the period to 0.5s is
100g
50g
150g
200g
The correct Answer is:C
T∝√m
Related Playlists
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - SIMPLE PENDULUM14videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED AND FORCED OSCILLATIONS2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - ENERGY OF A PARTICLE EXECUTING SHM9videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
View SolutionThree mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring. When is 0.4 kg mass is removed , the system oscillates with a period 2 s . When the 0.3 kg mass is also removed , the system will oscillates with a period
View SolutionThree masses of 500g, 300g and 100g are suspended at the end of a spring as shown and are in equilibrium. When the 500g mass is removed suddenly, the system oscillates with a period of 2s. When the 300g mass is also removed, it will oscillate with period T. Find the value of T.
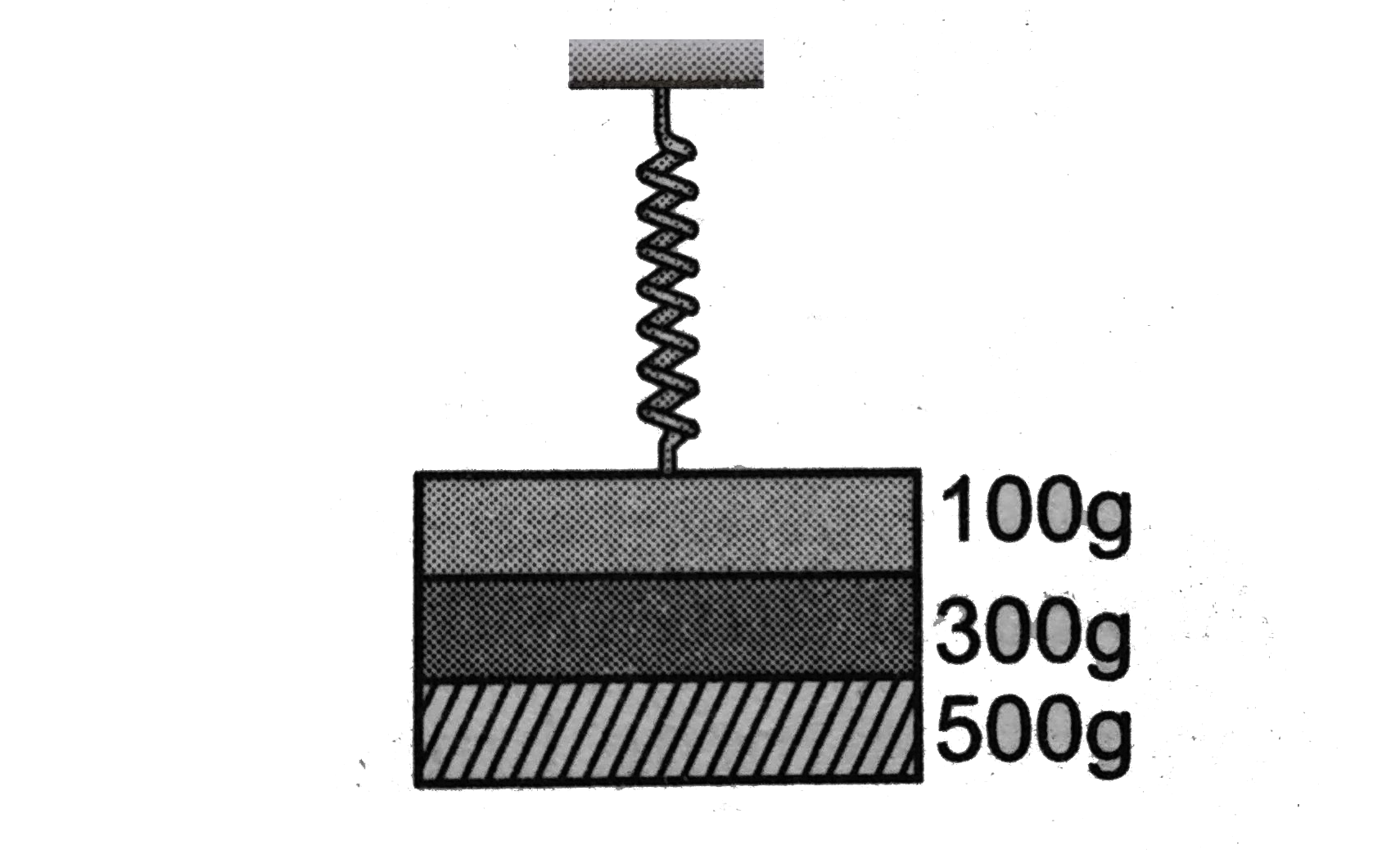 View Solution
View SolutionA srting of length l hangs freely from a rigid support under its own weight Calculate the time required by transverse waves to travel from the lower end to the upper end
View Solution1 kg weight is suspended to a weightless spring and it has time period T. If now 4 kg weight is suspended from the same spring the time period will be
View SolutionA mass m attached to a light spring oscillates with a period of 2 s. If the mass is increased by 2 kg, the period increases by 1 s. Then the value of m is
View SolutionThree masses 700 g , 500 g , and 400 g are suspended at the end of a spring a shown and are in equilibrium. When the 700 g mass is removed, the system oscillates with a period of 3 seconds, when the 500 gm mass also removed. It will oscillate with a period of
 View Solution
View SolutionA mass m attached to a spring oscillates with a period of 3s. If the mass is increased by 1kg the period increases by 1s. The initial mass m is
View SolutionThree masses 700g, 500g, and 400 g are suspended at the end of a spring a shown and are in equilibrium. When the 700 g mass is removed, the system oscillacts with a period of 3 seconds, when the 500 gm mass is also removed, it will oscillate with a period of
 View Solution
View SolutionA pan with set of weights is attached with a light spring. When disturbed, the mass-spring system oscillates with a time period of 0.6s When some additional weights are added then time period is 0.7s the extension caused by the additional weigts is approximately given by
View Solution


