A mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
3.1cm
6.2cm
9.3cm
12.4cm
The correct Answer is:B
To solve the problem step by step, we will use the information provided about the oscillation of the mass on the spring and the relationship between the period of oscillation, mass, and spring constant.
Step 1: Understand the relationship between period, mass, and spring constant
The period T of a mass-spring system in simple harmonic motion is given by the formula:
T=2π√mk
where:
- T is the period of oscillation,
- m is the mass attached to the spring,
- k is the spring constant.
Step 2: Rearrange the formula to find mk
We can rearrange the formula to express mk:
T2=4π2mk
Thus,
mk=T24π2
Step 3: Substitute the known value of the period
Given that T=0.5s, we can substitute this value into the equation:
mk=(0.5)24π2
Calculating (0.5)2:
(0.5)2=0.25
Now substituting this into the equation:
mk=0.254π2
Step 4: Calculate mk
Using π≈3.14:
π2≈9.86
Thus,
4π2≈39.44
Now substituting this value:
mk=0.2539.44≈0.00635
Step 5: Relate the stretch of the spring to the weight of the mass
When the mass is at rest, the force due to gravity mg is balanced by the spring force kδ:
kδ=mg
From this, we can express δ:
δ=mgk
Step 6: Substitute m in terms of k and δ
Using mk from Step 4:
δ=g⋅k⋅mkk=g⋅mk
Substituting the value of mk:
δ=g⋅0.00635
Step 7: Use g≈9.81m/s2
Now substituting the value of g:
δ=9.81⋅0.00635≈0.0625m
Step 8: Convert to centimeters
To convert meters to centimeters:
δ=0.0625m×100=6.25cm
Final Answer
The stretch in the spring when the mass is allowed to hang at rest is approximately:
δ≈6.25cm
The period T of a mass-spring system in simple harmonic motion is given by the formula:
T=2π√mk
where:
- T is the period of oscillation,
- m is the mass attached to the spring,
- k is the spring constant.
We can rearrange the formula to express mk:
T2=4π2mk
Thus,
mk=T24π2
Given that T=0.5s, we can substitute this value into the equation:
mk=(0.5)24π2
Calculating (0.5)2:
(0.5)2=0.25
Now substituting this into the equation:
mk=0.254π2
Using π≈3.14:
π2≈9.86
Thus,
4π2≈39.44
Now substituting this value:
mk=0.2539.44≈0.00635
When the mass is at rest, the force due to gravity mg is balanced by the spring force kδ:
kδ=mg
From this, we can express δ:
δ=mgk
Using mk from Step 4:
δ=g⋅k⋅mkk=g⋅mk
Substituting the value of mk:
δ=g⋅0.00635
Now substituting the value of g:
δ=9.81⋅0.00635≈0.0625m
To convert meters to centimeters:
δ=0.0625m×100=6.25cm
The stretch in the spring when the mass is allowed to hang at rest is approximately:
δ≈6.25cm
Topper's Solved these Questions
Similar Questions
A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation , the spring becomes upstretched . Find the speed when the spring is stretched by 0.20 cm . (Take , g=π2m/s2)
View SolutionA body of mass 2 kg suspended through a vertical spring executes simple harmonic motionof period 4s. If the oscillations are stopped and the body hangs in equillibrium, find the potential energy stored in the spring.
View Solution
Knowledge Check
A mass m suspended from a vertical spring oscillates with a period of 4 s. The mass is then kept at rest. Through what dis"tan"ce the spring will be stretched ? [Take pi^(2)=10]
A3 mB4 mC5 mD6 mA body of mass 4.9 kg hangs from a spring and oscillates with a period 0.5 s. On the removal of the body, the spring is shortened by (Take g=10ms−2,π2=10)
A0.625 cmB0.63 cmC6.25 cmD63 cmWhen a mass of 5 kg is suspended from a spring of negligible mass and spring constant K, it oscillates with a periodic time 2π. If the mass is removed, the length of the spring will decrease by
AgK metreBg metreC2π metreDmK metre
When a mass m attached to a spring it oscillates with period 4s. When an additional mass of 2 kg is attached to a spring, time period increases by 1s. The value of m is :-
View SolutionA mass m attached to a spring oscillates with a period of 3s. If the mass is increased by 1kg the period increases by 1s. The initial mass m is
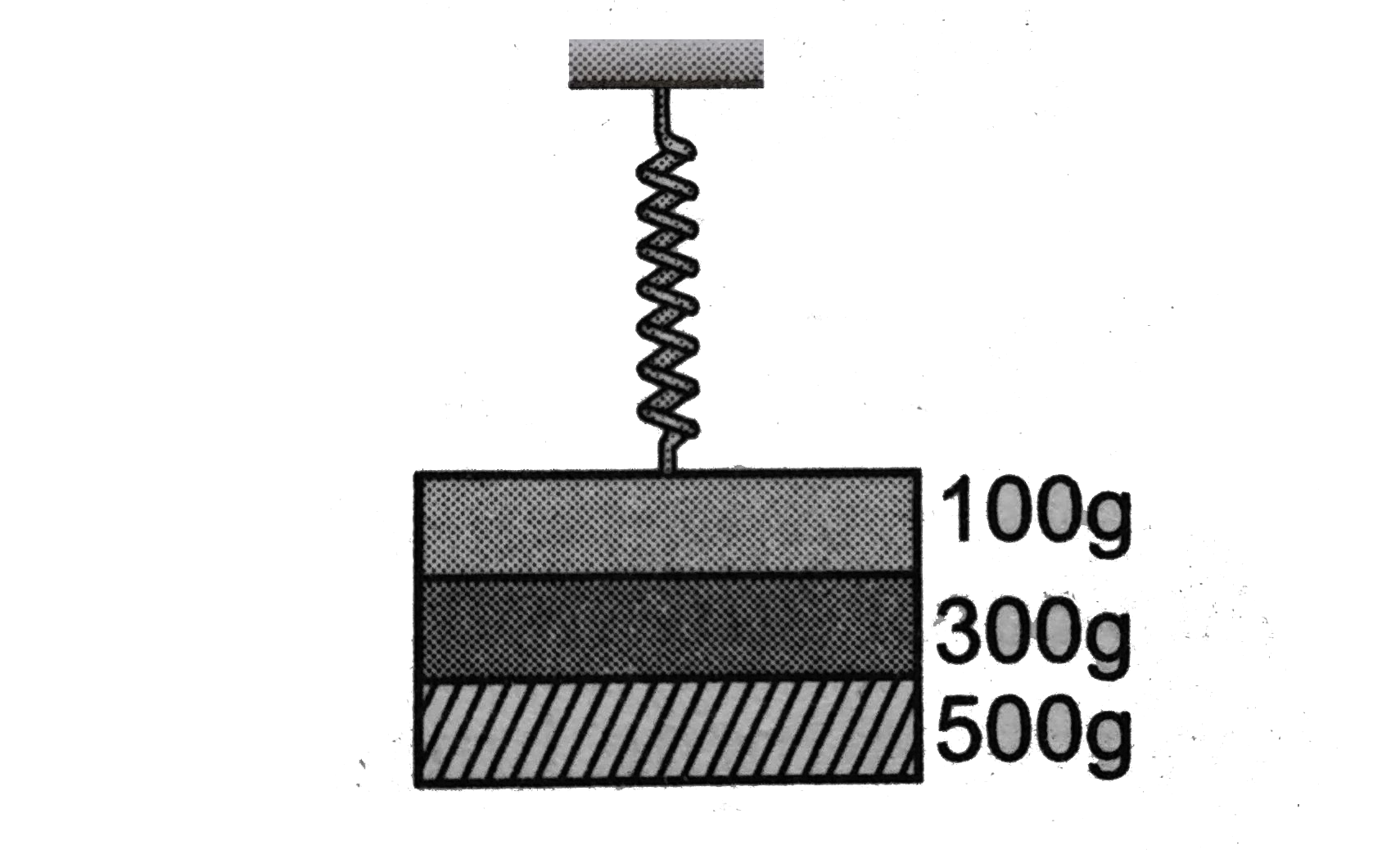
View SolutionThree masses of 500g, 300g and 100g are suspended at the end of a spring as shown and are in equilibrium. When the 500g mass is removed suddenly, the system oscillates with a period of 2s. When the 300g mass is also removed, it will oscillate with period T. Find the value of T.
View SolutionThree mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring. When is 0.4 kg mass is removed , the system oscillates with a period 2 s . When the 0.3 kg mass is also removed , the system will oscillates with a period
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View Solution