Four mass less spring whose force constant are 2k,2k,k and 2k respectively are attached to a mass M kept on a friction less plate (as shown in figure) if the mass M is displaced in the horizontal direction then the frequency of oscillation of the system is
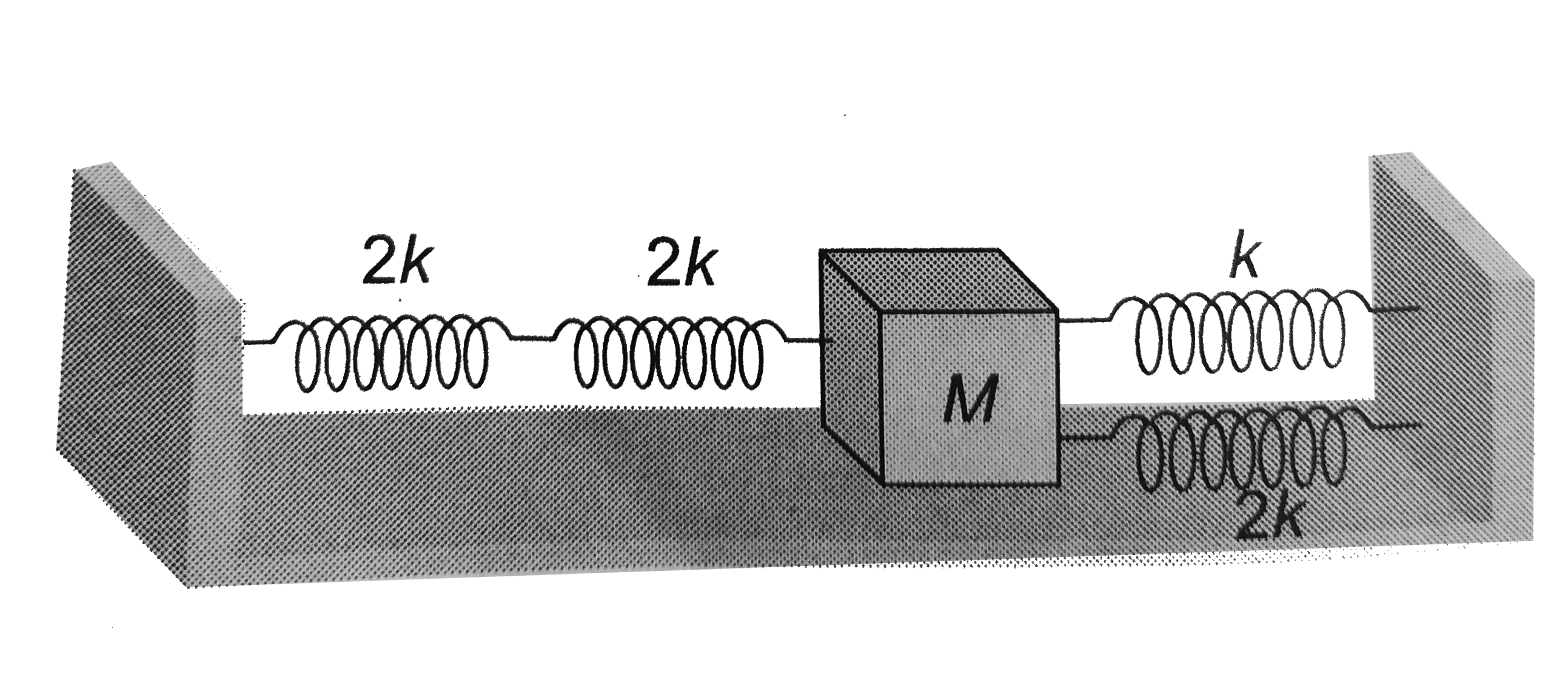
12π√K4M
12π√4KM
12π√K7M
12π√7KM
The correct Answer is:B
f=12π√Keffm
Related Playlists
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - SIMPLE PENDULUM14videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED AND FORCED OSCILLATIONS2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - ENERGY OF A PARTICLE EXECUTING SHM9videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
Four massless springs whose force constants are 2k,2k, k and 2k, respectively, are attached to a mass M kept on a frictionless plane (as shown in figure), If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is
 View Solution
View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is
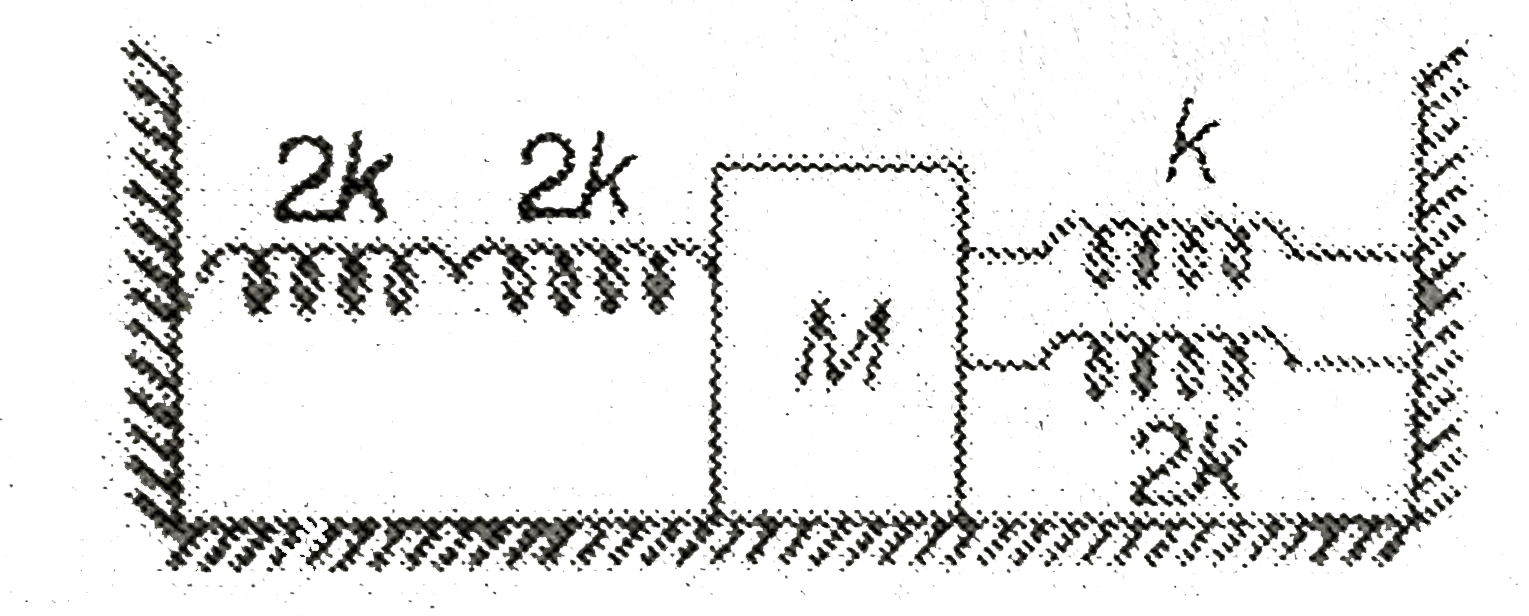 View Solution
View SolutionFour massless spring whose force constant are 2k,2k,k and 2k respectively are attached to a mass M kept on a frictions plate (as shown in figure) if the mass M is displaced in the horizontal direction then the frequency of oscillation of the system is
 View Solution
View SolutionFour massless springs whose force constants are 2k,2k,k and 2k respectively are attached to a mass M kept on a fricaionless plane (as shown in figure). If the mass M is displaced in the horizontal directions, then the frequency of the system.
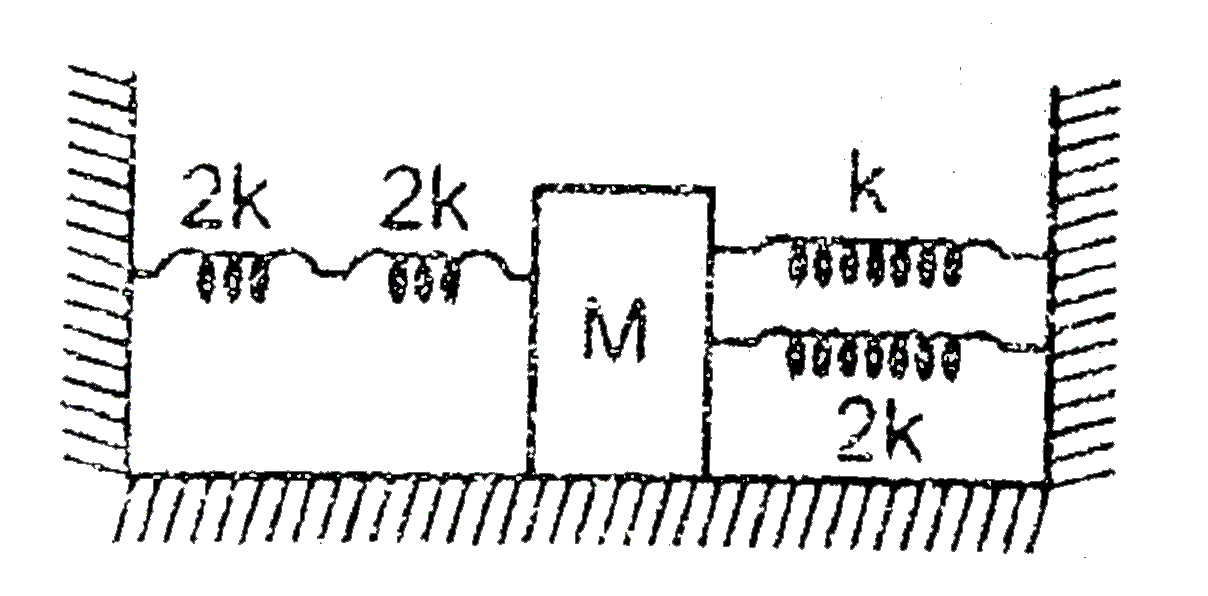 View Solution
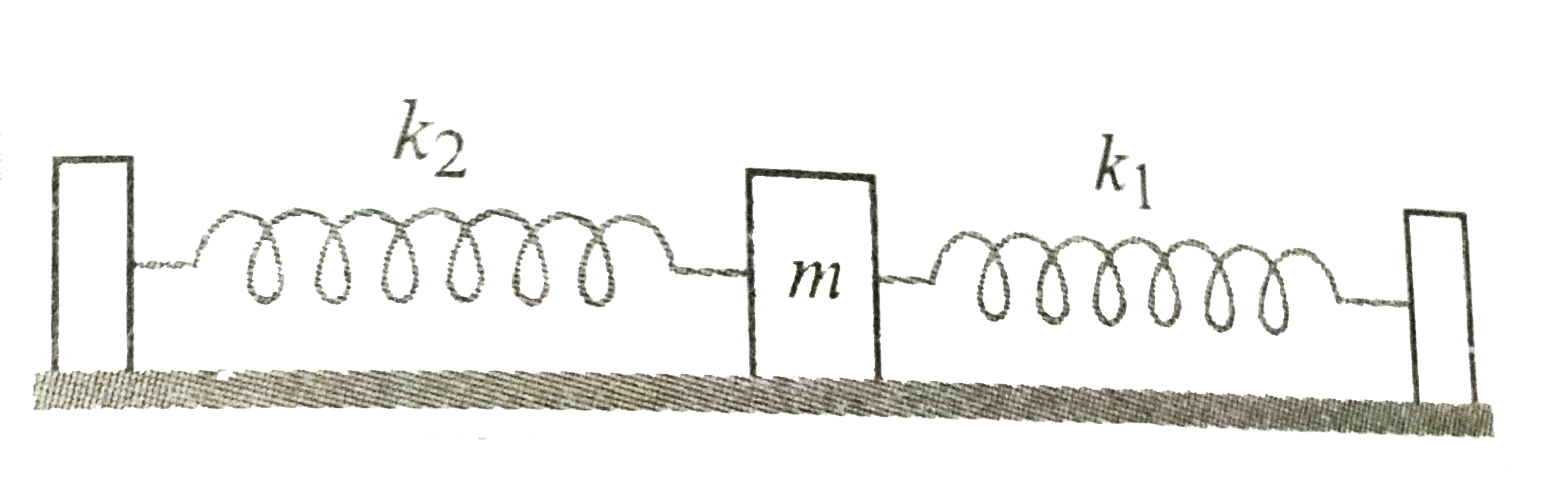
View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
 View Solution
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
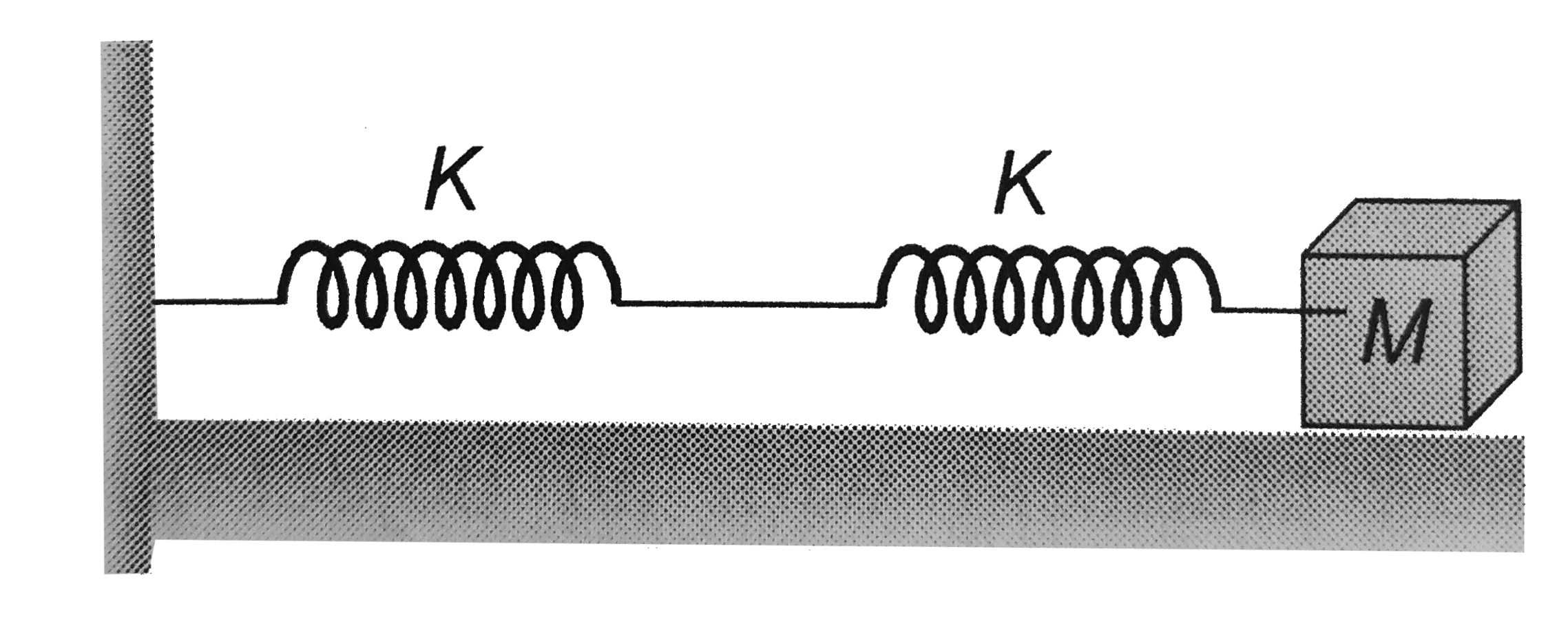 View Solution
View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-
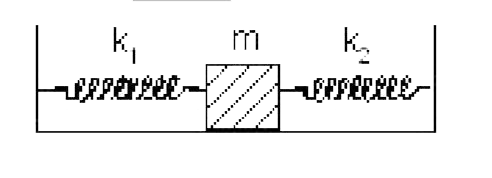 View Solution
View SolutionTwo springs of force constants k1 and k2 are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f=12π√k1k2(k1+k−(2))m
[Hint: Let the mass be displaced by x and the clamped end of the second spring by x′. Then mf = −k1(x−x′). Considering the first spring and the mass as a single system we have mf =−k2x′]View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View Solution


