Two blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
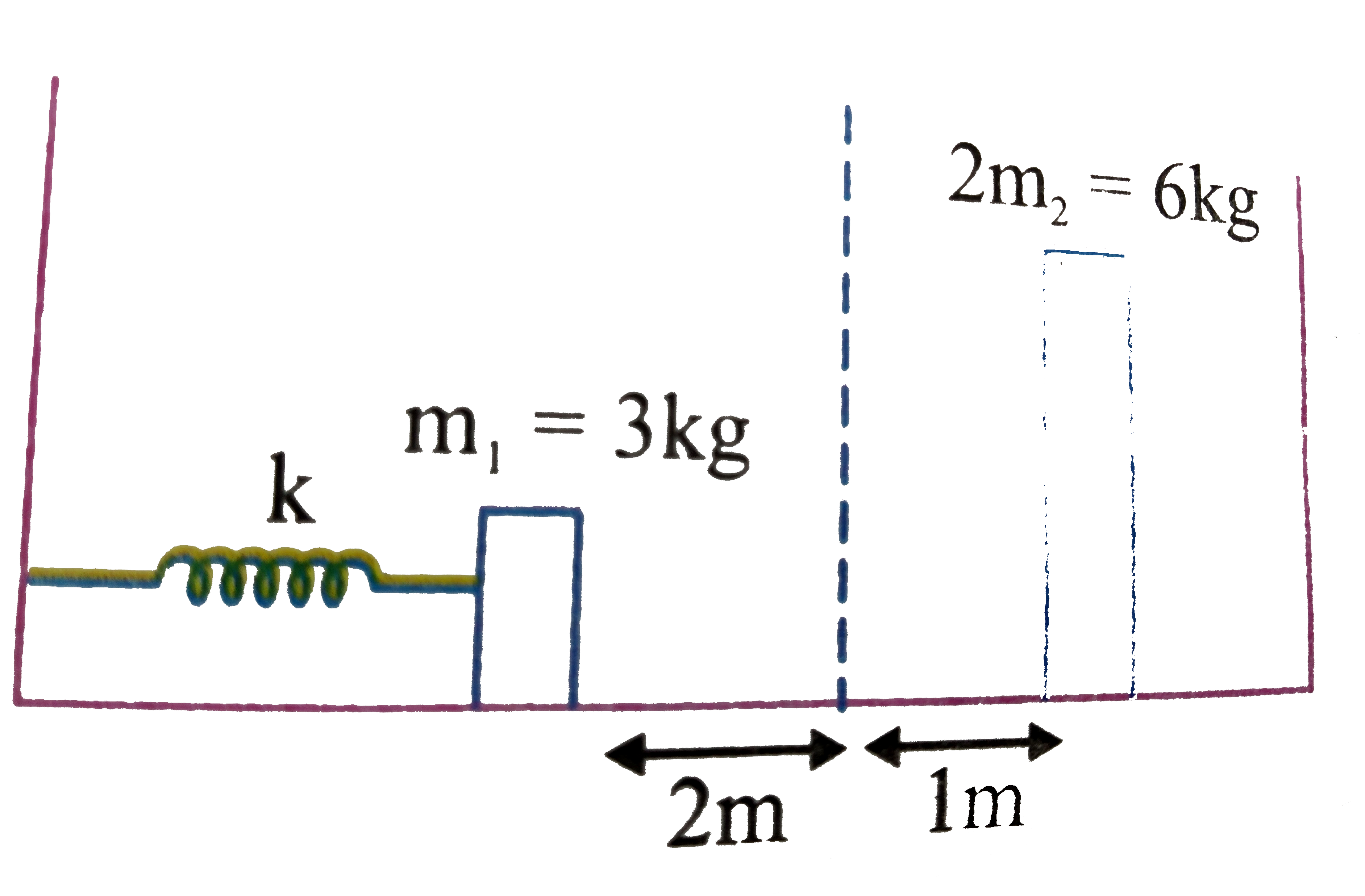
The amplitude of resulting oscillation after the collision is:
1√2m
1√3m
√2m
√3m
The correct Answer is:C
After collision angular frequency of oscillation has changed however the instantaneous position of block does not change. Also equilibrium position is still ar relaxed length of spring.
Hence x=1m
Now angular velocity ω'=√k(m1+m2),
ω'=√9009=10
Velocity =ω'√A'2−x2or10=10√A'2−12
Hence A'=√2m
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-II
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-III
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View Solution
Knowledge Check
Two blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
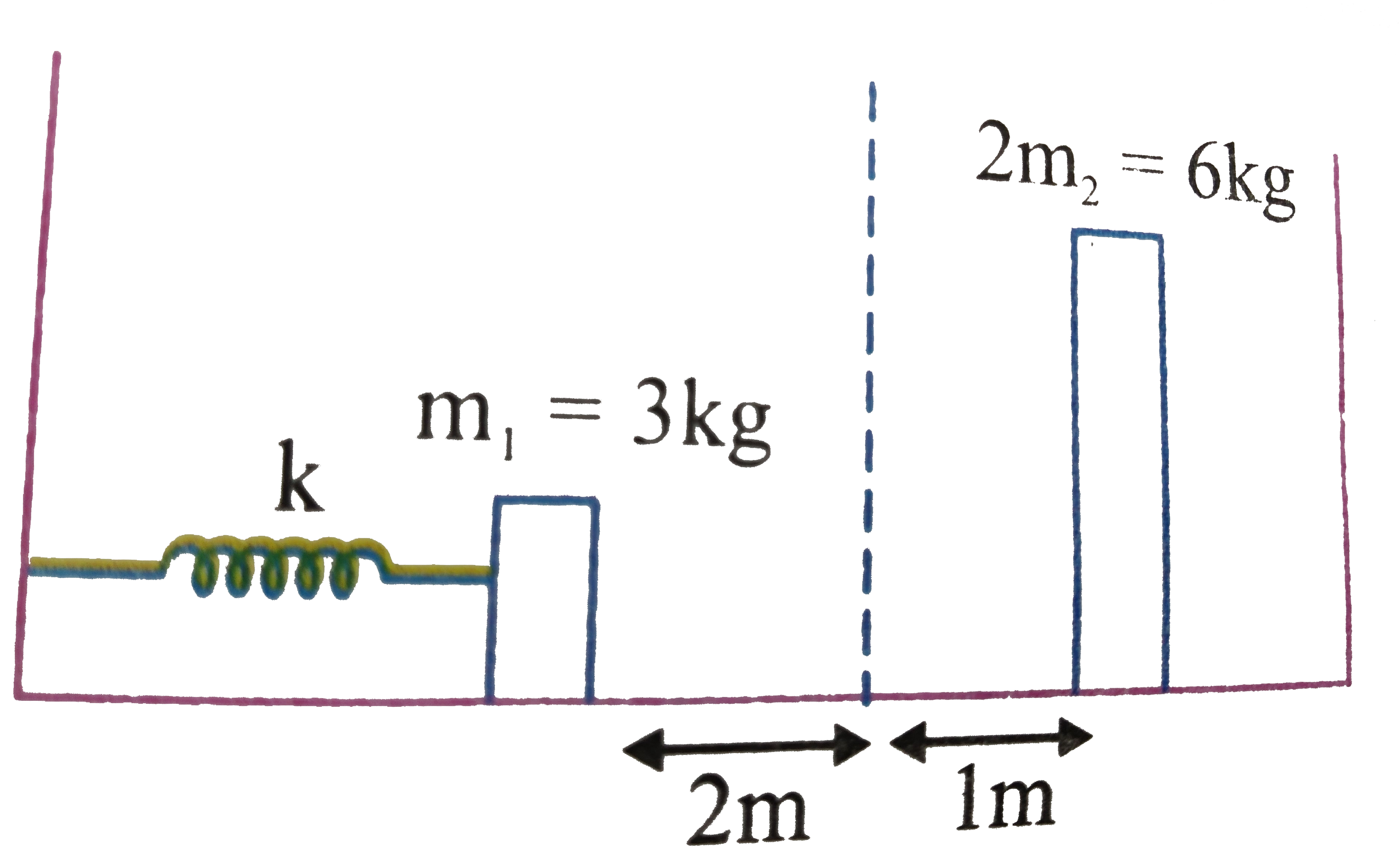
The common velocity of the blocks after collision isA10m/sB30m/sC15m/sD2m/sTwo blocks of masses 3kg block is attached to a spring with a force constant, kk=900N/ma which is compressed 2m initially from its equilibrium position. When 3kg mass is released, it strikes the 6kg mass and the two stick togther in an inelastic collision.
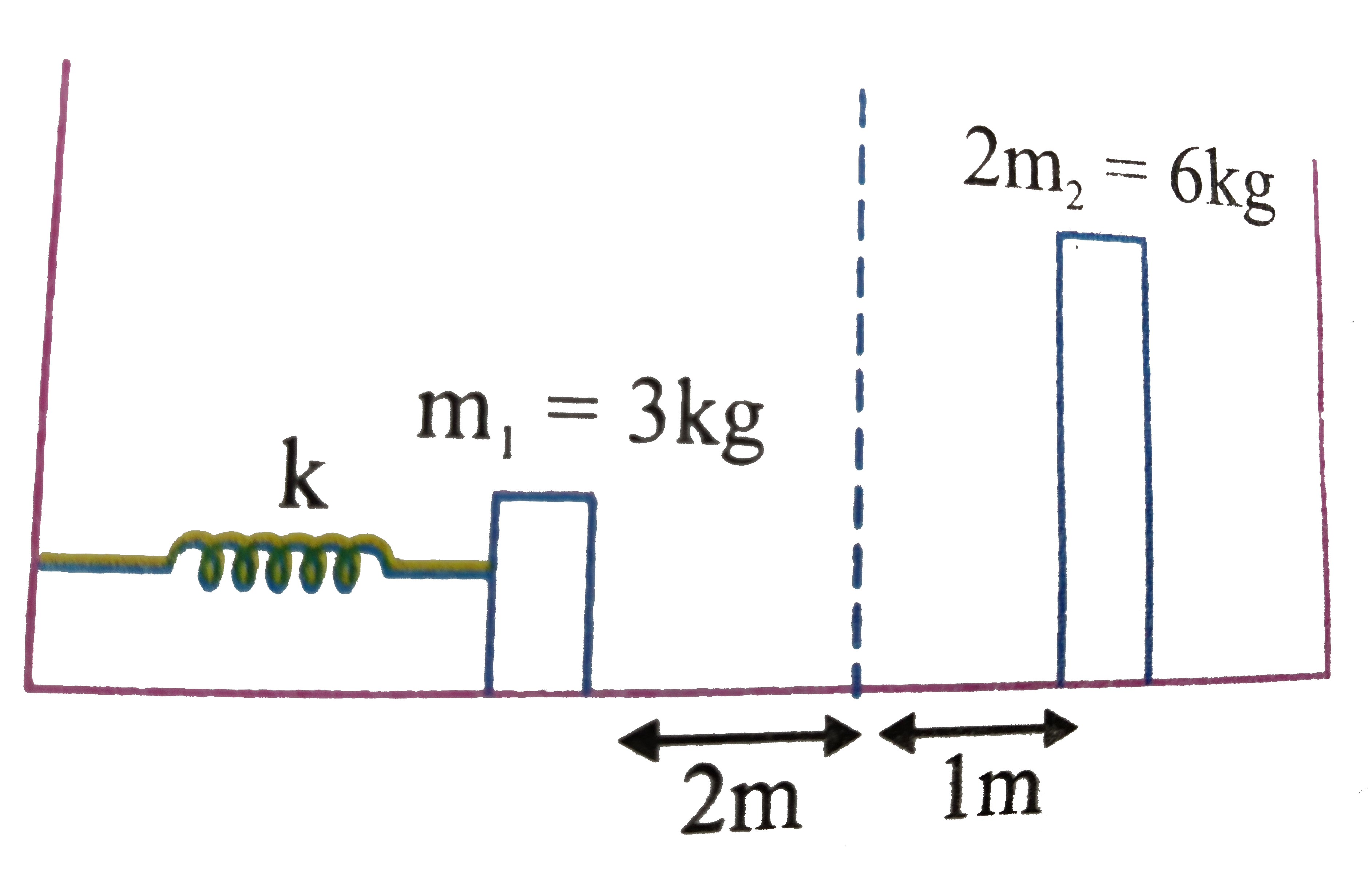
The velocities of a particle executing S.H.M. are 30cm/s and 16cm/s when its displacements are 8cm and 15cm from the equilibrium position. then its amplitude of oscillation in cm is:A25B21C17D13Two blocks of masses 3kg and 6kg rest on a horizontal smooth surface. The 3kg block is attached to a spring with a force constant k=900Nm−1 which is compressed 2m from beyond the equilibrium position. 3kg mass strikes the 6kgmass and two stick together-
 Avelocity of the combined masses immediately arter the collision is 10ms−1Bvelocity of the conbined masses immediately after the collision is 5ms−1CAmplitude of the resulting oscillation is √2mDAmplitude of the resulting oscillation is √5/2m
Avelocity of the combined masses immediately arter the collision is 10ms−1Bvelocity of the conbined masses immediately after the collision is 5ms−1CAmplitude of the resulting oscillation is √2mDAmplitude of the resulting oscillation is √5/2m
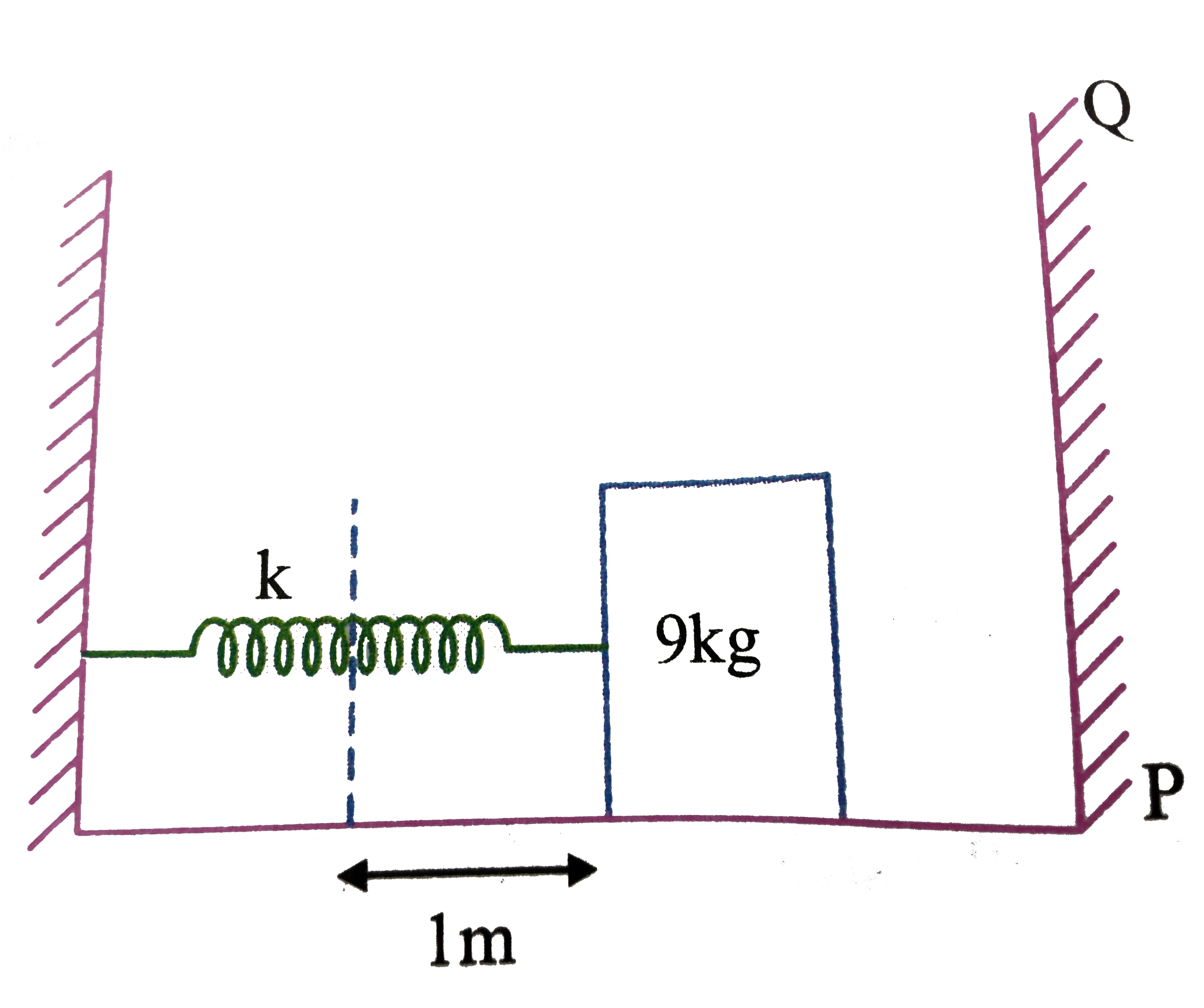
A block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
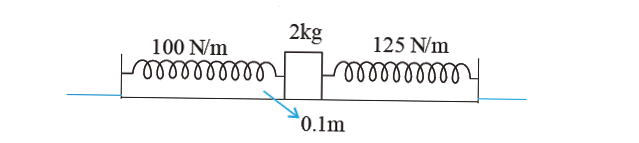
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
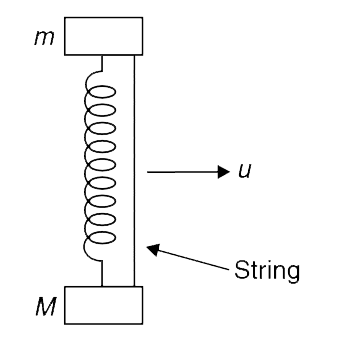
View SolutionTwo blocks of masses m=2kgandm=8kg are connected to a spring of force constant K=1kN/m. The spring is compressed by 20cm and the two blocks are held in this position by a string. The system is placed on a horizontal smooth surface and given a velocity u=3m/s perpendicular to the spring. The string snaps while moving. Find the speed of the block of mass m when the spring regains its natural length.
View SolutionTwo blocks of masses 3 kg and 6kg rest on horizontal smooth surface. The 3 kg block is attached to a spring with a long constant k=900Nm−1 which is compressed 2m from beyond 1m from mean position. 3kg mass strikes the 6 kg mass and the two stick together.

View SolutionA block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View Solution
