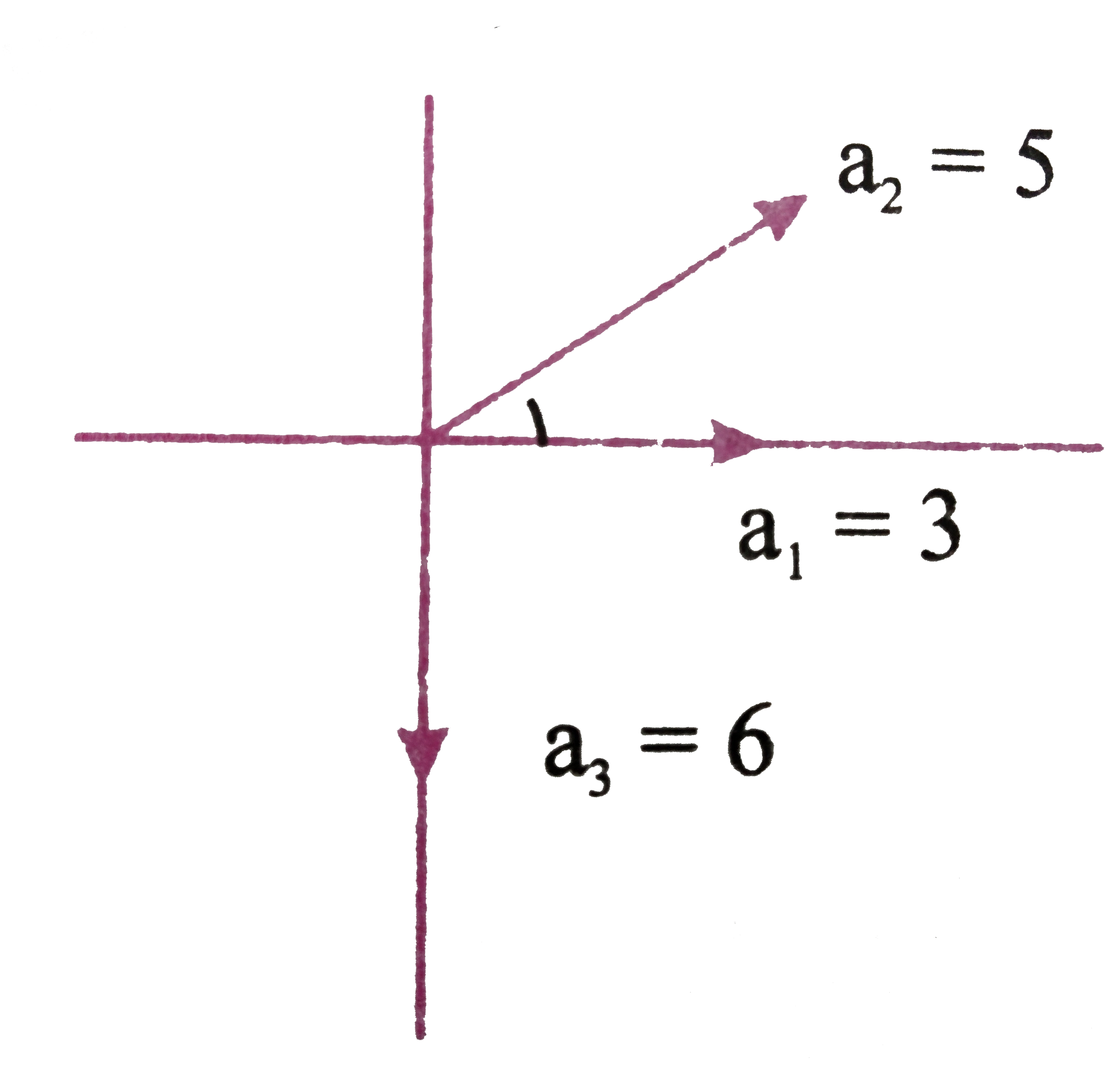
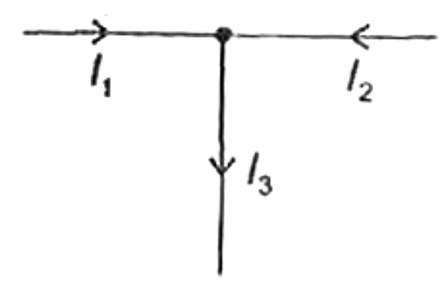
Using graphical means find an amplitude $a$ of oscillations resulting from the superposition of the following oscillations of the same direction $:$
$(a)$ $x_{1} = 3.0 cos (ω t + π / 3), x_{2} = 8.0 sin (ω t + π / 6),$
$(b)$ $x_{1} = 3.0 cos ω t, x_{2} = 5.0 cos (ω t + π / 4), x_{3} = 6.0 sin ω t .$

$14$

$7$

$4$

$2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

The resultant amplitude due to super position of $x_{1} = sin ω t, x_{2} = 5 sin (ω t + 37^{\circ})$ and $x_{3} = - 15 cos ω t$ is $:$
A17
B21
C13
DNone of these
Find the resultant amplitude of the following simple harmonic equations $:$
$x_{1} = 5 sin ω t$
$x_{2} = 5 sin (ω t + 53^{\circ})$
$x_{3} = - 10 cos ω t$
A5
B10
C15
D20