A bob of mass 2m hanges by a string attached to the block of mass m of a spring blocks syetem. The whole arrangement is in a state of equilibrium. The bob of mass 2m is pulled down slowely by a distance x0 and released.
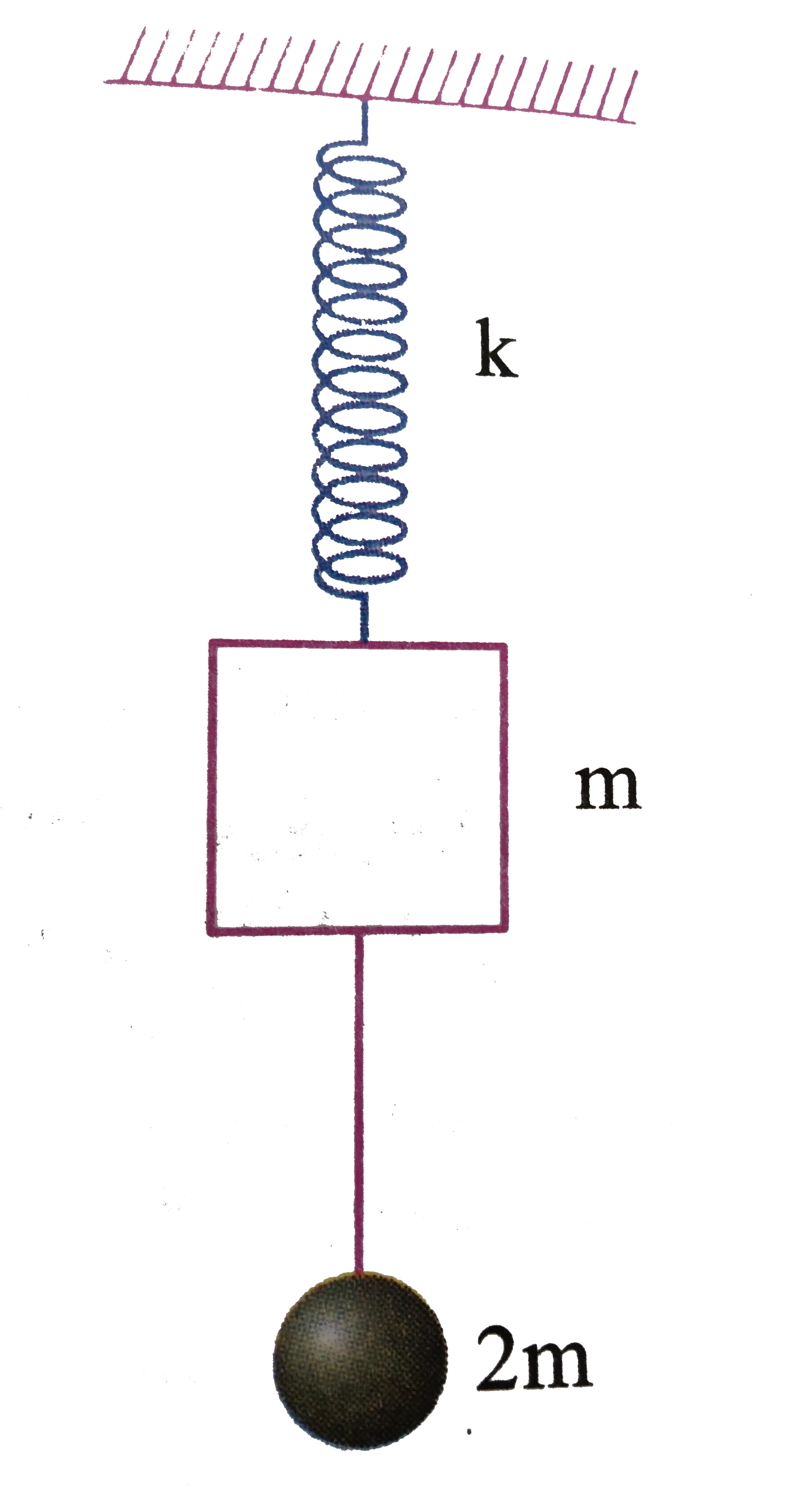
For x0=3mgk, maximum tension in string is 4mg
For x0>3mgk, minimum tension in string is mg
Frequency of oscillation of system is 12π√k3m, for all non-zero values of x0
The motion will remain simple harmonic for x0≥3mgk
The correct Answer is:A, D
(A) 2(6mg−T−mg−ma)−(T−2mg−2ma)=0
12mg−3T=0
T=4mg
(B) Kx+T+mg=ma
2mg−T=2ma for T=0,a=g
⇒x=0
As particle is released x0 below equilibriums so it will go x0 above equilibrium i.e. at x=0⇒Tmin=0
(C ) & (D) for x0>3mgk it will be longer SHM as string will slack
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:ASSERTION & REASON QUESTIONS
Explore 13 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:NCERT BASED QUESTIONS
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
In the fig shown, a block of mass M is attached to the spring and another block of mass 2M has been placed over it. The system is in equilibrium. The block are pushed down so that the spring compresses further by 9MgK. System is released
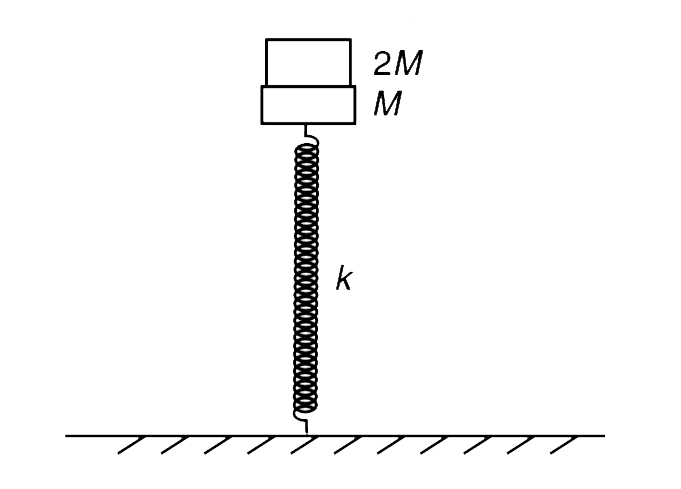
(a) At what height above the position of release, the block of mass 2M will lose contact with the other block? (b) What is maximum height attained by 2M above the point of release?
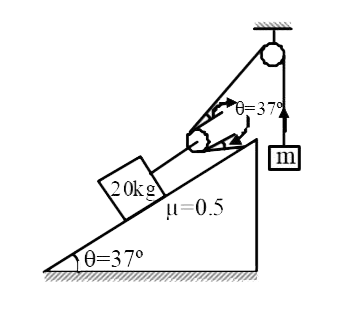
View SolutionAs shown in figure pulley is ideal and strings are massless.If mass m of hanging block is the minimum mass to set the equilibrium of system, then -
View Solution
Knowledge Check
In Fig. a pulley is shown which is frictionless and a ring of mass m can slide on the string without any friction. One end of the string is attached to point B and to the other end, a block 'P' of mass m is attached. The whole system lies in vertical plane.
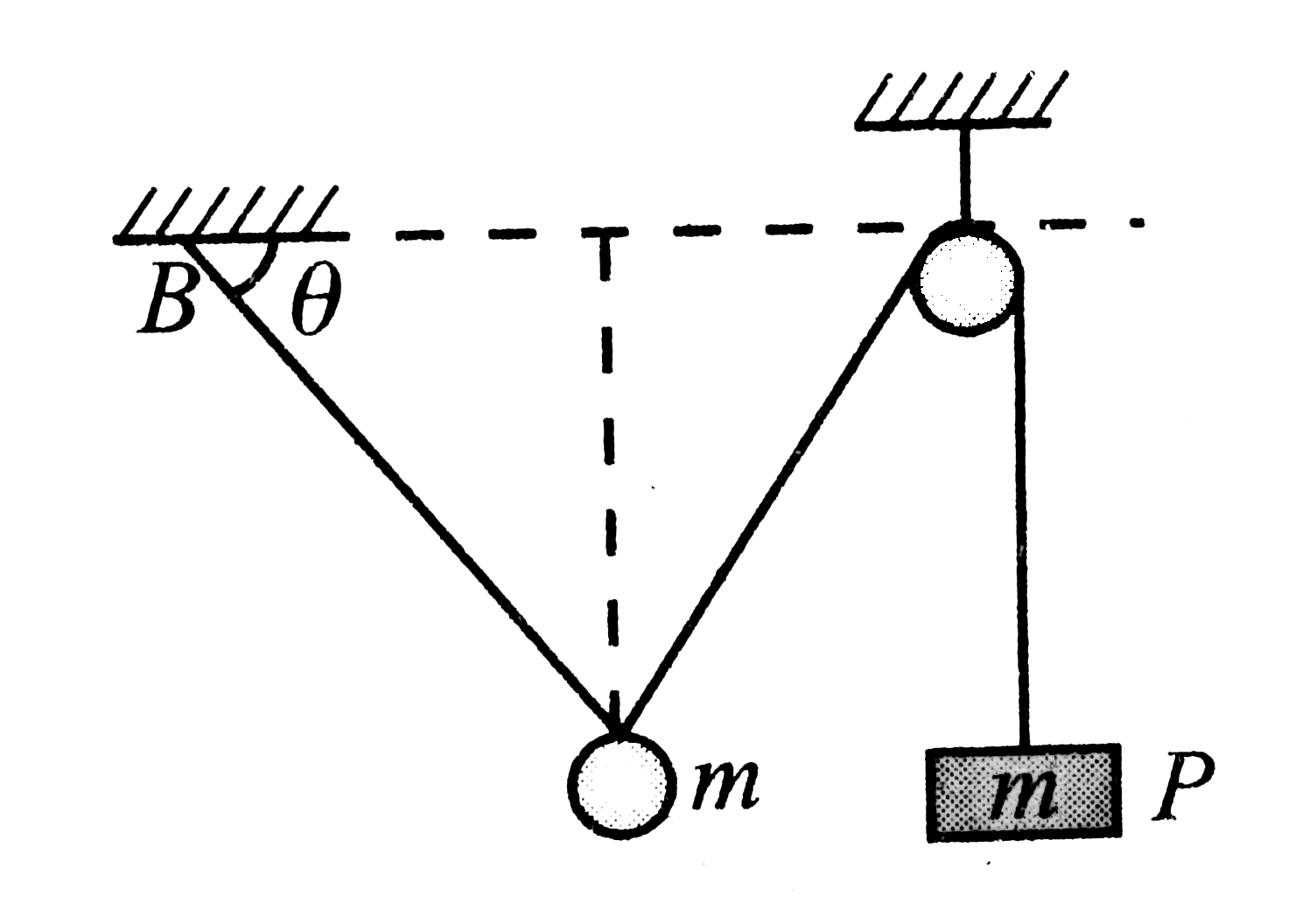 Now another block 'C' of same mass m is attached to the block '13' and system is released from rest. If a1 and a2 are the magnitudes of initial accelerations of ring and blocks, respectively, then Aa1+a2=gBa1+2a2=gCa1=2a2D2a1=a2
Now another block 'C' of same mass m is attached to the block '13' and system is released from rest. If a1 and a2 are the magnitudes of initial accelerations of ring and blocks, respectively, then Aa1+a2=gBa1+2a2=gCa1=2a2D2a1=a2Two blocks (1 and 2) of equal mass m are connected by an ideal string (see figure shown) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants k1 and k2 such that k1>k2
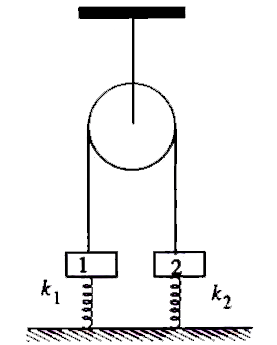
Initially, both springs are unstretched. The block 1 is slowly pulled down a distance x and released. Just after the release the possible values of the magnitude of the acceleration of the blocks a1 and a2 can be–AEither (a1=a2=(k1+k2)x2m) or (a1k1xm−ganda2=k2xm+g)B(a1=a2=(k1+k2)x2m) onlyC(a1=a2=(k1−k2)x2m) onlyD(a1=a2=(k1−k2)x2m) or (a1=a2=(k1k2)x(k1+k2)m−g)A block A of mass m is attached at one end of a light spring and the other end of the spring is connected to another block B of mass 2m through a light string as shown in the figure. A is held and B is in static equilibrium. Now A is released. The acceleration of A just after that instant is a . In the next case, B is held and A is in static equilibrium. Now when B is released, its acceleration immediately after the release is b . The value of a/b is (pulley, string and the spring are massless).
 A0BundefinedC2D12
A0BundefinedC2D12
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
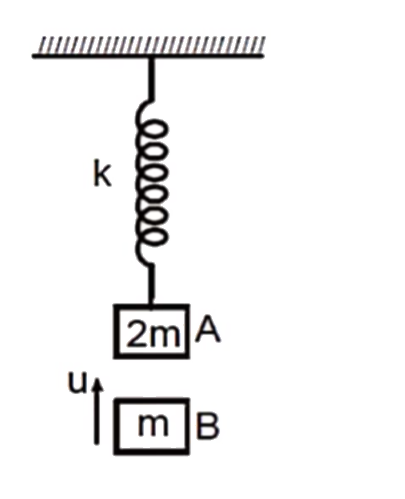
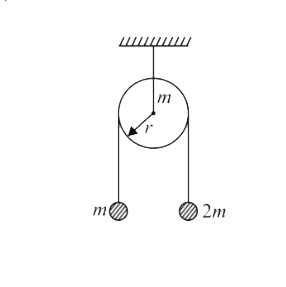
View SolutionAs shown in the figure, two bobs of masses m & 2m are tied by a massless string which is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob of mass 2m starts falling vertically. When it has covered distance of h, the angular speed of the wheel will be:
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View Solution

